A rod AB of length 2m is hinging at point A and its other end B is attached to a platform on which a point of mass m is kept. Rod rotates about point A maintain angle θ=30∘ with the vertical in such a way that platform remain horizontal and revolves on the horizontal circular path. If the coefficient of static friction between the block and platform is μ=0.1 then find the maximum angular velocity in rads−1 of rod so that the block does not slip on the platform (g=10ms−2)
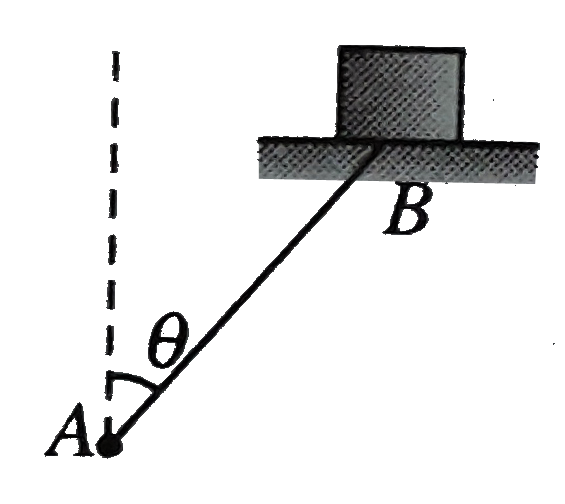
The correct Answer is:1
N=mgμN=mrω2
μmg=m2sinθω2
⇒ω=√μg2sinθ=√0.1×102×sin30=1rads−1

Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - True And False
4 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Single correct answer type
13 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Linked Comprehension
52 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
When a person walls on a rought surface, the frictional force exerted by the surface on the person is opposite to the direction of his motion.
View SolutionA ship of mass 3×107kg initially at rest, is pulled by a force of 5×105N through a distance of 3m. Assuming that the resistance due to water is negligible, the speed of the ship is
View SolutionA monkey of mass m clings a rope to a slung over a fixed pulley .The opposite end of the rope is tried to a weight of mass M tying on a horizontal table is μ Find the acceleration of weight and the tension of the rope for two cases .The monkey move downward with respect to the rope with an acceleration b.

The acceleration of weight is
View SolutionA block is placed on an inclined plane moving towards right horizontally with an acceleration a0=g. The length of the plane AC=1m. Friction is absent everywhere. Find the time taken (in seconds) by the block to reach from C to A.
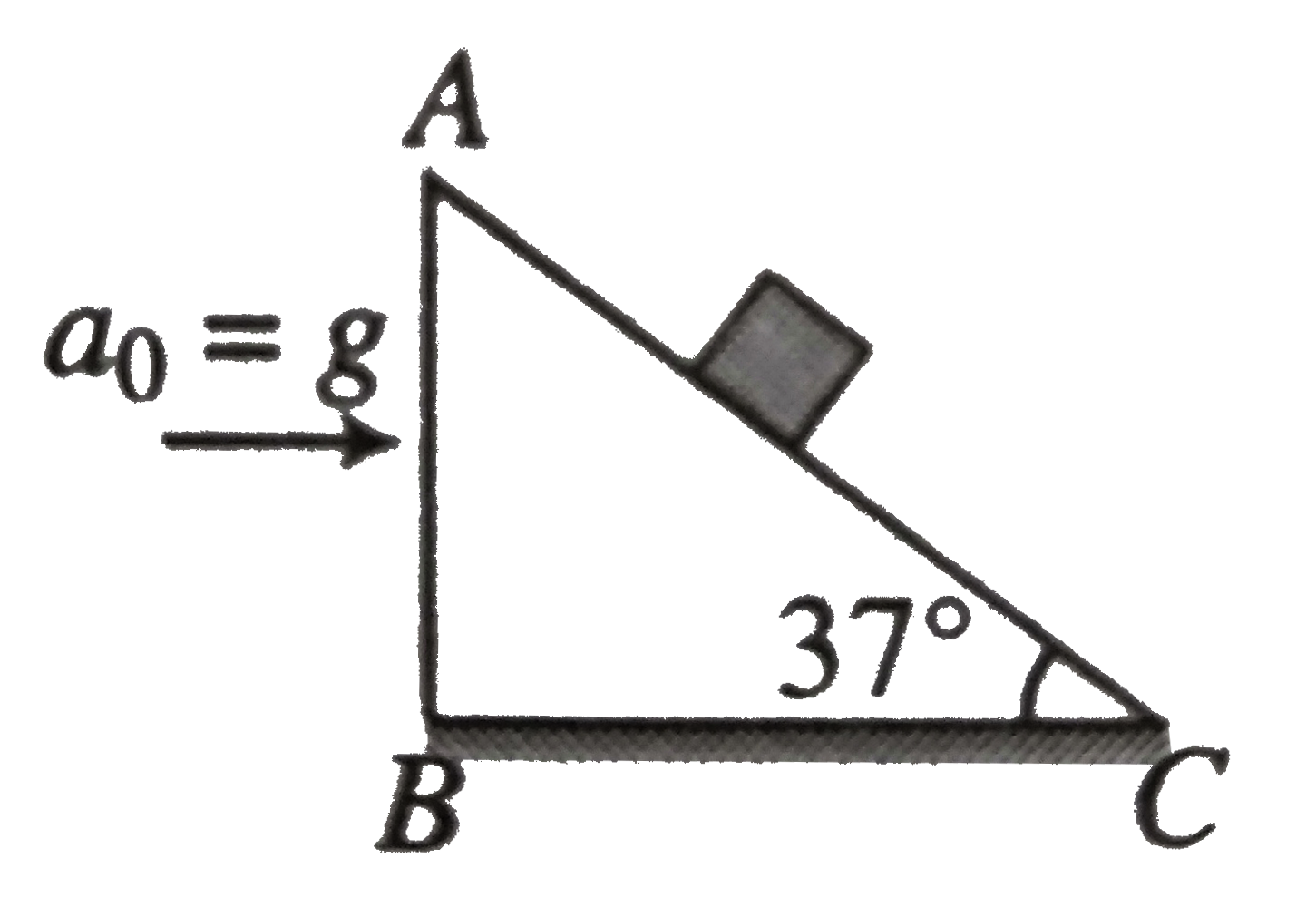
View SolutionTwo soap bubbles A and B are kept in a closed chamber where the air is maintained at pressure 8N/m2.The radii of bubbles A and B are 2cm and 4cm, respectively. Surface tension of the soap-water used to make bubbles is 0.04N/m. Find tha ratio nB/nA, where nA and nB are the number of moles of air in bubbles A and B, respectively. [Neglect the effect of gravity.]
View SolutionTwo masses each of m are attached at mid point B and end point C of massless rod AC which is hinged at A . It is released from horizontal position as shown. Find the force at hinge A when rod becomes vertical. .
View SolutionA uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle theta with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed V in the horizontal plane then the angular momentum of the rod about the axis is:
View SolutionAB is a mass less rigid rod of length 2l. It is free to rotate in vertical plane about a horizontal axis passing through its end A. Equal point masses (m each) are stuck at the centre C and end Bof the rod. The rod is released from horizontal position. Write the tension in the rod when it becomes vertical.
View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity omega as shown in the figure. The rod maintains a constant angle theta with the vertical. What will be the horizontal component of angular momentum of the rod about the point of suspension in terms of m , omega , l and theta .
View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity omega as shown in the figure. The rod maintains a constant angle theta with the vertical. What angle will the rod make with the vertical
View SolutionTwo particles each of mass m are attached at end points of a massless rod AB of length l. Rod is hinged at point C as shown. Rod is released from rest from horizontal position. At the instant when rod reaches its vertical position as shown, which of the following is / are correct:
View SolutionA block is placed on a horizontal platform. The system is making horizontal oscillations about a fixed point with a frequency of 0.5 Hz. The maximum amplitude of oscillation if the block is not to side on the horizontal platform, is (Coefficient of friction between the block and the platform = 0.4)
View SolutionA block is placed on a horizontal platform. The system is making horizontal oscillations about a fixed point with a frequency of 0.5Hz. The maximum amplitude of oscillation if the block is not to slide on the horizontal platform, is (Coefficient of friction between the block and the platform = 0.4)
View SolutionA uniform rod AB of mass m is hinged at one A. The rod is kept in horizontal position by a massless string tied to point B. The reaction of the hinge on the end A of the rod at the instant, when string is cut is mg/x. Where 'x' is

View Solution
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle θ with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed V in the horizontal plane then the angular momentum of the rod about the axis is:
View Solution
