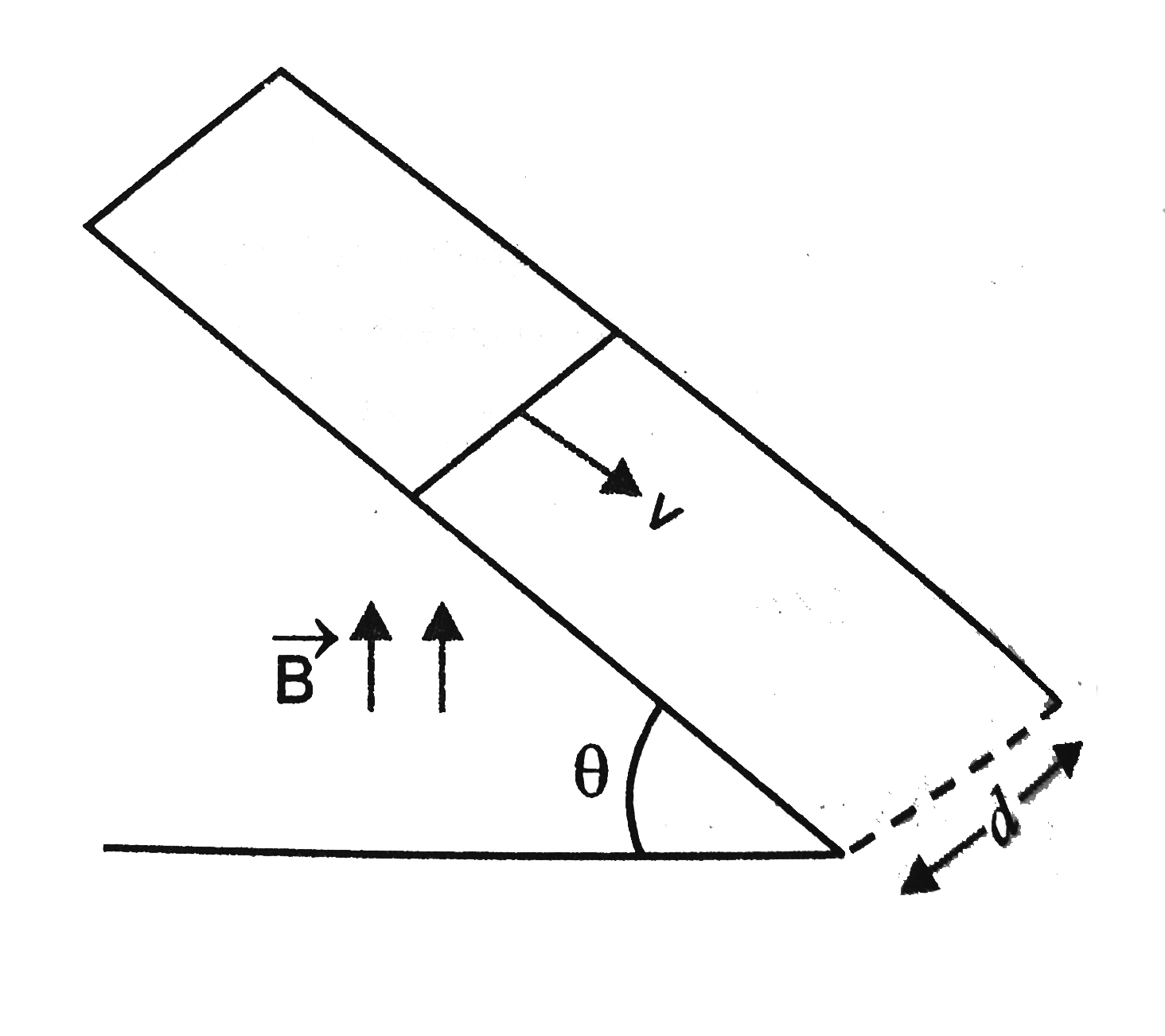
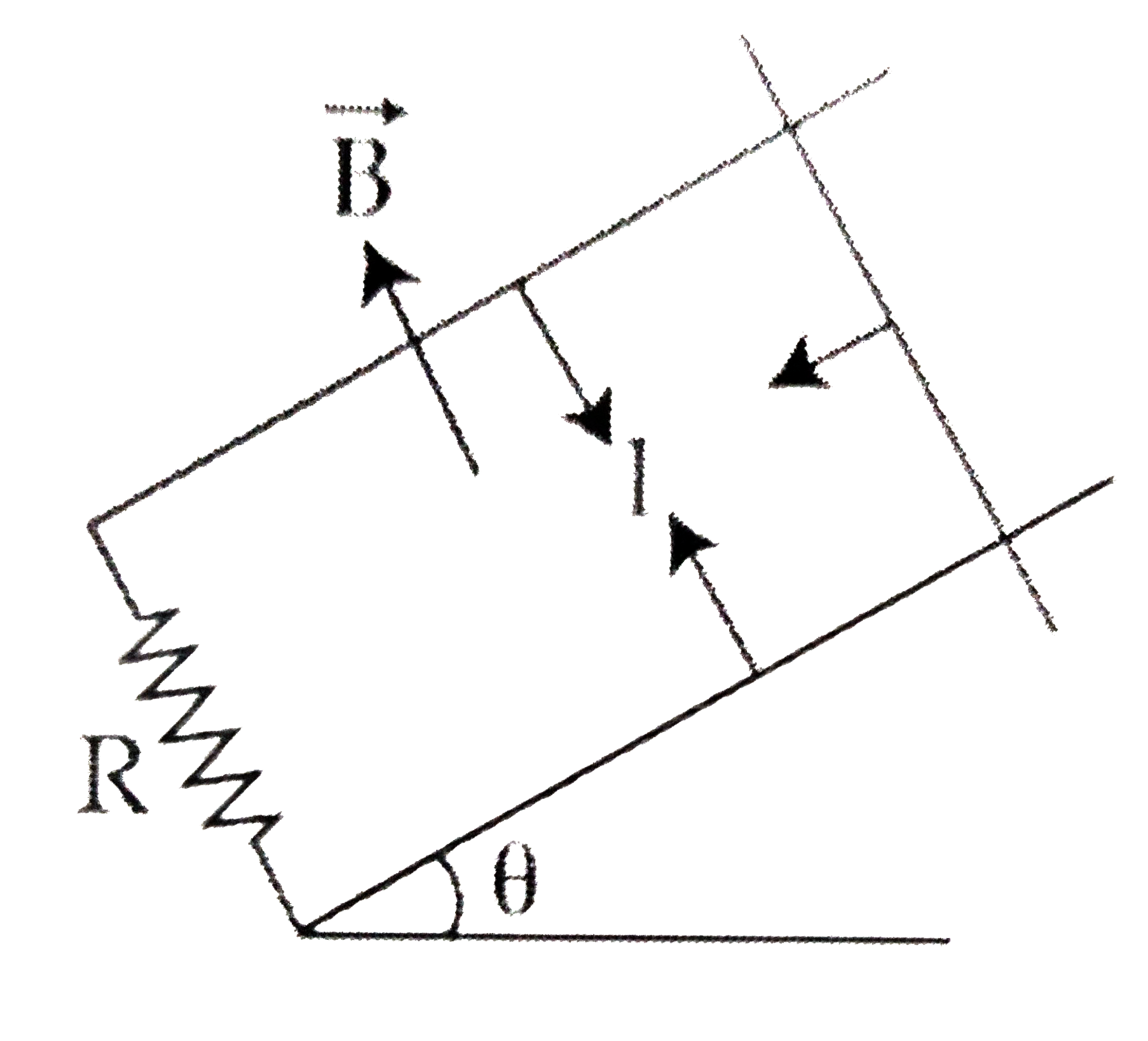
A rod of mass m and resistance R slides smoothly over two parallel perfectly conducting wires kept sloping at an angle θ with respect to the horiaontal, Fig. The circuit is closed through a perfert conductor at the top. There is a constant magnetic field B along the vertical direction. If the rod is initially at rest, find the velocity of the rod as a function of time.
The set up is shown in Fig. Component of weight of rod down the incline = mg sin θ. Component of magnetic field up the incline = B cos θ. Therefore, force on the rod due to magnetic field
=BIl=(Bcosθ)(Bcosθd.υ)Rd=B2d2(cosθ)2υR
∴ The equation of motion of the rod can be written as
mdυdt=md2xdt2=mgsinθ−B2d2R(cosθ)2υ
∴dυdt=gsinθ−B2d2mR(cosθ)2υ
or dυdt+B2d2mR(cosθ)2υ=gsinθ
∴υ=gsinθB2d2cos2θ/mr+A exp[−b2d2mR(cos2θ)t]
where A is a constant that can be determined from initial conditions (A = 1).
υ=mRgsinθB2d2cos2θ[1−exp(−B2d2mR(cos2θ)t)]
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Solved Examples (b)1videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Short Answer Qusetions2videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
- BOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise191videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - II Focus multiple choice question5videos
ELECTROMAGNETIC WAVES
Similar Questions
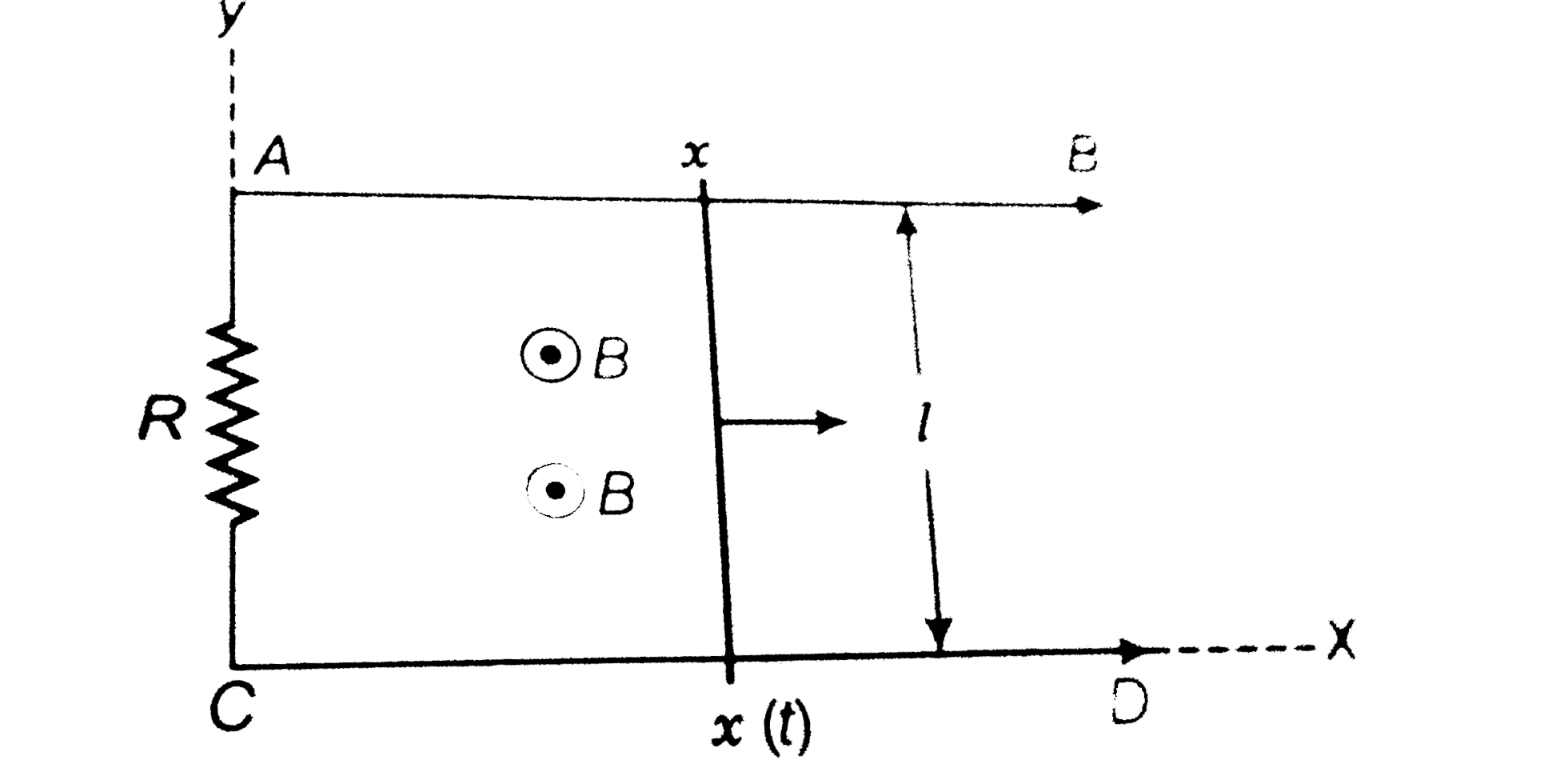
A conducting wire XY of mass M and negligible resistance slides smothly on two parallel conducting wires as shown in figure. The closed circuit has a resistance R due to AC. AB and CD are perfect conductors. There is a magnetic field B=B(t)ˆk
 View Solution
View SolutionA uniform rod AB of mass m and length l is placed over two smooth conducting rails P and Q. If the witch shown as closed at t=0, find the velocity of rod AB as a function of time.
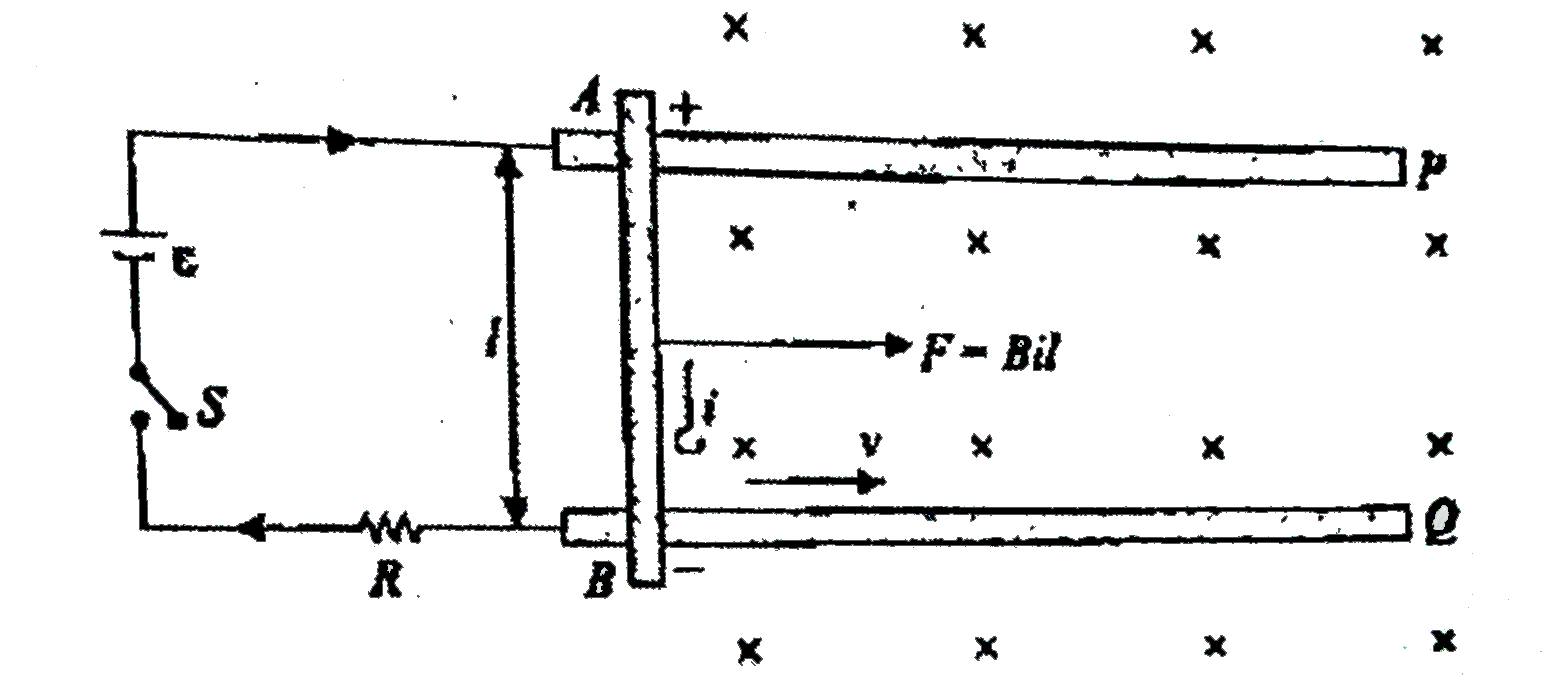 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A copper rod of mass m slides under gravity on two smooth parallel rails l distance apart set at an angle θ to the horizontal. At the bottom, the rails are joined by a resistance R.

There is a uniform magnetic field perpendicular to the plane of the rails. the terminal valocity of the rod isAmgRtanθB2l2BmgRcotθB2l2CmgRsinθB2l2DmgRcosθB2l2 - Question 2 - Select One
A copper rod of mass m slides under gravity on two smooth parallel rails l distance apart set at an angle θ to the horizontal. At the bottom, the rails are joined by a resistance R.

There is a uniform magnetic field perpendicular to the plane of the rails. the terminal valocity of the rod isAmgRcosθB2l2BmgRsinθB2l2CmgRtanθB2l2DmgRcotθB2l2 - Question 3 - Select One
A metallic rod of mass m and resistance R is sliding over the 2 conducting frictionless rails as shown in Fig. An infinitely long wire carries a current I0. The distance of the rails from the wire are b and a respectively.
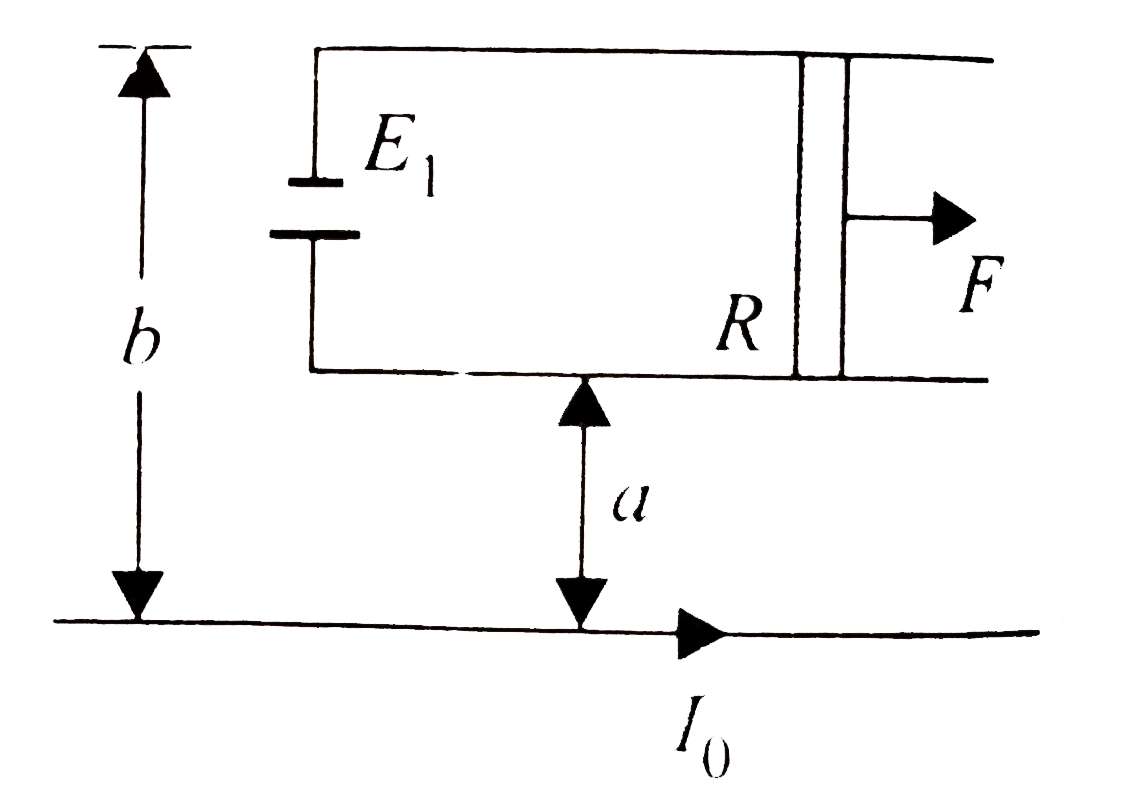
Find the value of current in the circuit if the rod slides with constant velocity v0A1R{E−μ0I0v02π1n∣∣∣ba∣∣∣}B1R{E+μ0I0v02π1n∣∣∣ba∣∣∣}C1R{E−μ0I0v0π1n∣∣∣ba∣∣∣}DNone of these
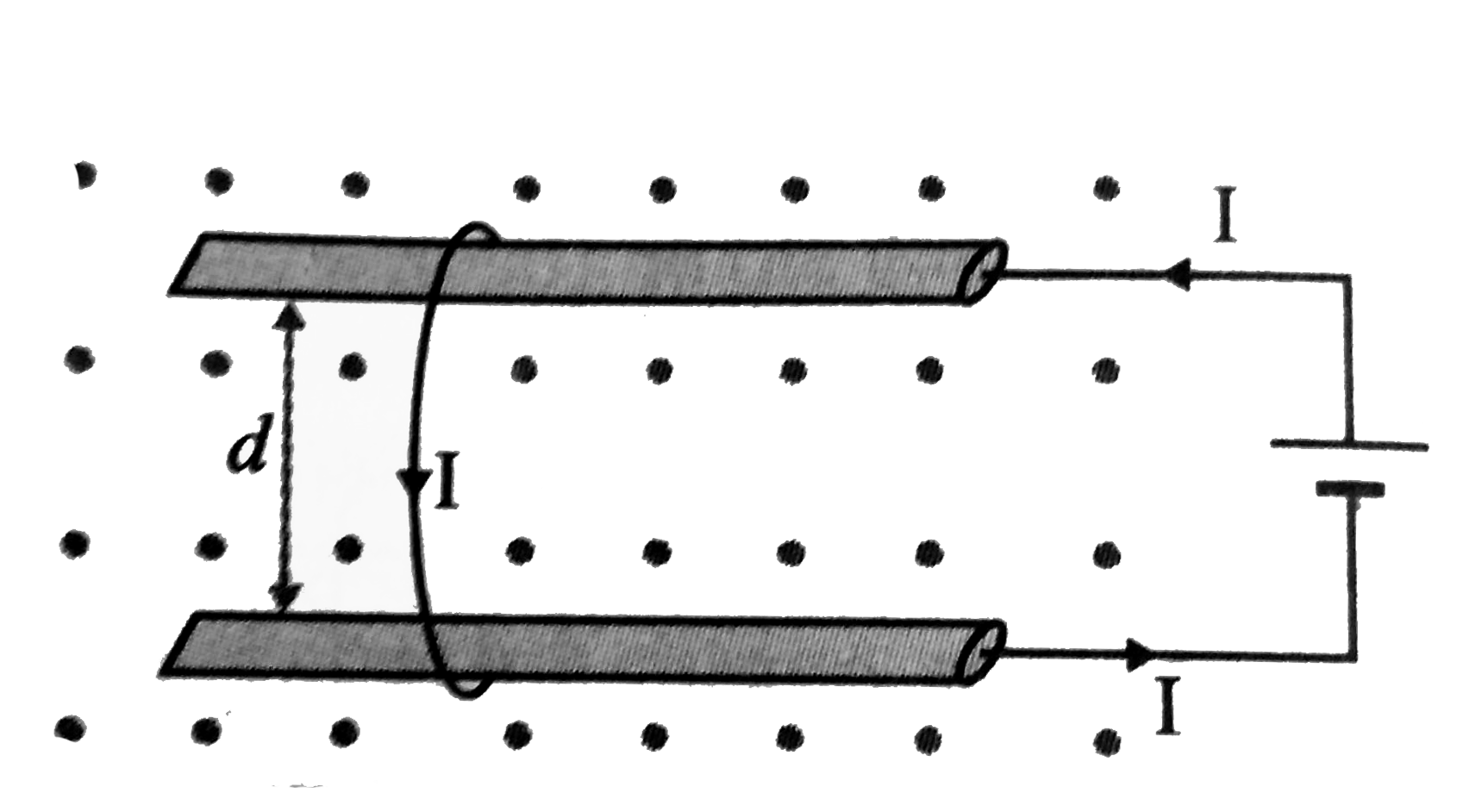
a copper rod of mass m slides under gravity on two smooth parallel rails with separation I and set at an angle of θ with the horiziontal at the bottom rails are joined by resistance R. There is a uniform magnetic field B normal to the plane of the rails as shown in the figure The terminal speed of the copper rod is :View SolutionA metal wire of mass m slides without friction on two horizontal rails spaced distance d-apart as shown in figure. The rails are situated in a uniform magnetic field B, directed vertically upwards, and a battery is sending a current I through them. Find the velocity of the wire as a function of time, assuming it to be at rest initially.
 View Solution
View SolutionA rod of mass m and resistance r is placed on fixed, resistanceless, smooth conducting rails (closed by a resistance R) and it is projected with an initial velocity u.Find its velocity as a function of time.
 View Solution
View SolutionTwo long parallel horizontal rails a, a distance d aprt and each having a risistance λ per unit length are joing at one end by a resistance R. A perfectly conduction rod MN of mass m is free to slide along the rails without friction (see figure). There is a uniform magnetic field of induction B normal to the plane of the paper and directed into the paper. A variable force F is applied to the rod MN such that, as the rod moves a constant current flows through R.
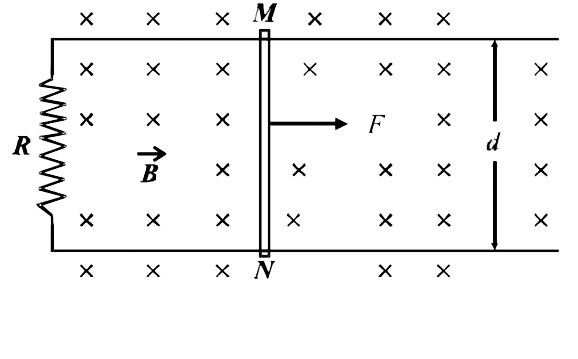
(i) Find the velocity of the rod and the applied force F as function of the distance x of the rod from R.
(ii) What fraction of the work done per second by F is converted into heat?View SolutionA conducting wire of length l and mass m can slide without friction on two parallel rails and is connected to capacitance C. The whole system lies in a magnetic field B and a constant force F is applied to the rod. Then
View Solution

