A round current-carrying loop lies in the plane boundary between magnetic and vacumm. The permeability of th emagnetic is equal to $μ$ Find the magnetic induction $B$ at an arbitary point on the axis of the loop if in the absence of th e magnetic the magnetic induction at the same point becomes equal to $B_{0}$ . Genralize the obtained result to all poins of the field.

Text Solution

Verified by Experts

The medium $I$ is vacumm and contains a circular current carrying coil with current $I$ . The medium $I I$ is a megentic with permeabitliy $μ$ . The boundary is the plane $z = 0$ and the coil is the plane $z = 1$ . To find the magnitude induction we note that the effect of the magentic medium can be written as due to an image coil in $I I$ as far as the medim $I$ is concerned. On the other hand, the induction is $I I$ as far as the medium $I$ is concerned, On the other hand, the induction is $I I$ can be written as due t the coil in $I$ , carrying a different current. It is sufficient to consider the far away fields and ensure that the boundary conditions are satisfied there. Now for actual coil in medium $I$ .

$B_{r} = - \frac{2 p_{m} cos θ'}{r^{3}} . (\frac{μ_{0}}{4 π}) . B_{0} = \frac{p_{m} sin θ'}{r^{3}} (\frac{μ_{0}}{4 π})$
so, $B_{2} = \frac{μ_{0} P m}{4 π} (2 {cos}^{2} θ' - {sin}^{2} θ')$ and $B_{x} = \frac{μ_{0} p_{m}}{4 π} (- 3 sin θ' cos θ')$
where $p_{m} = I (π a^{2}), a$ = radius of the coil.
Similarly due to the image coil,
$B_{x} = \frac{μ_{0} p'}{4 π} (2 {cos}^{2} θ' - {sin}^{2} θ), B_{x} = \frac{μ_{0} p'}{4 π} (3 sin θ' cos θ'), p'_{m} = I' (π a^{2})$
As fas as the medium $I I$ is concered, we write similarly
$B_{z} = \frac{μ_{0} p''_{m}}{4 π} (2 {cos}^{2} - {sin}^{2} θ'), B_{x} = \frac{μ_{0} p''_{m}}{4 π} (- 3 sin θ' cos θ') . p''_{m} = I'' (π a^{2})$
The boundary conditions are, $p_{m} + p'_{m} = p_{m}$ (from $B_{1 n} - B_{2 n}$ )
$p_{m} + p'_{m} = - \frac{1}{μ} p_{m}$ (from $H_{1 t} = H_{2 t}$ )
Thus, $I = \frac{2 μ}{μ + 1} I, I' = \frac{μ - 1}{μ + 1} I$
In the limit, when the coil is on the boundary, the magnetic filed envery where can be obtained by taking the current to be $\frac{2 μ}{μ + 1} I$ . Thus, $\to B = \frac{2 μ}{μ + 1} - \to B_{0}$

In the loop shown, the magnetic induction at the point O

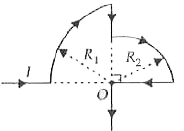A $\frac{μ_{0} I}{8} (\frac{R_{1} - R_{2}}{R_{1} R_{2}})$
B $\frac{μ_{0} I}{8} (\frac{R_{1} + R_{2}}{R_{1} R_{2}})$
C $\frac{μ_{0} I}{8} (\frac{R_{1} R_{2}}{R_{1} + R_{2}})$
Dzero
In the loop shown, the magnetic induction at the point 'o' is

A $\frac{μ_{0} I}{8} (\frac{R_{1} - R_{2}}{R_{1} R_{2}})$
B $\frac{μ_{0} I}{8} (\frac{R_{1} + R_{2}}{R_{1} R_{2}})$
C $\frac{μ_{0} I}{8} (\frac{R_{1} R_{2}}{R_{1} + R_{2}})$
D0
The magnetic induction at a point on axis of a short magnetic dipole is
A $\frac{π_{0}}{4 π} \frac{2 M}{r^{3}}$
B $\frac{π_{0}}{4 π} \frac{3 M}{r^{3}} 1$
C $\frac{π_{0}}{4 π} \frac{M}{r^{3}}$
D $\frac{π_{0}}{4 π} \frac{2 M^{2}}{r^{3}}$