A semicircular disc of mass M and radius R is free to rotate about its diameter. The moment of inertia of semicircular disc about a line perpendicular to its plane through centre is
34MR2
MR22
MR23
MR24
The correct Answer is:B
To find the moment of inertia of a semicircular disc of mass M and radius R about a line perpendicular to its plane through the center, we can follow these steps:
Step 1: Understand the Geometry
The semicircular disc can be visualized as half of a full circular disc. The moment of inertia of a full circular disc about an axis through its center and perpendicular to its plane is given by the formula:
Ifull=12MR2
Step 2: Moment of Inertia of the Semicircular Disc
Since we are dealing with a semicircular disc, we need to find the moment of inertia for just half of the full disc. The mass of the semicircular disc is M, and its radius is R. The moment of inertia for the semicircular disc about an axis through its center and perpendicular to its plane is:
Isemicircular=12Ifull=12(12MR2)=14MR2
Step 3: Final Result
Thus, the moment of inertia of the semicircular disc about a line perpendicular to its plane through the center is:
I=14MR2
Summary
The moment of inertia of a semicircular disc about a line perpendicular to its plane through the center is:
14MR2
The semicircular disc can be visualized as half of a full circular disc. The moment of inertia of a full circular disc about an axis through its center and perpendicular to its plane is given by the formula:
Ifull=12MR2
Since we are dealing with a semicircular disc, we need to find the moment of inertia for just half of the full disc. The mass of the semicircular disc is M, and its radius is R. The moment of inertia for the semicircular disc about an axis through its center and perpendicular to its plane is:
Isemicircular=12Ifull=12(12MR2)=14MR2
Thus, the moment of inertia of the semicircular disc about a line perpendicular to its plane through the center is:
I=14MR2
The moment of inertia of a semicircular disc about a line perpendicular to its plane through the center is:
14MR2
Topper's Solved these Questions
Similar Questions
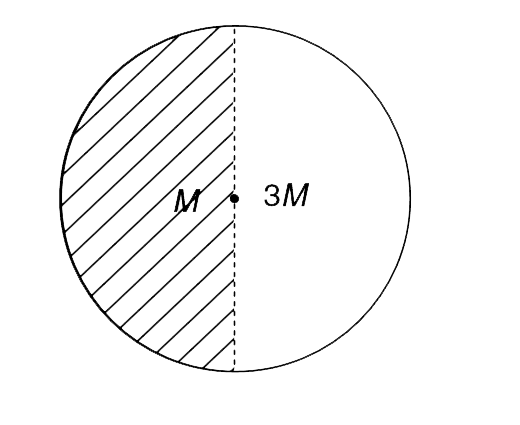
Two uniform semicircular discs, each of radius R, are stuck together to form a disc. Masses of the two semicircular parts are M and 3M. Find the moment of inertia of the circular disc about an axis perpendicular to its plane and passing through its centre of mass.
View SolutionA rectangular piece of dimension l×b is cut out of central portion of a uniform circular disc of mass m and radius r. The moment of inertia of the remaining piece about an axis perpendicular to the plane of the disc and passing through its centre is :
View Solution
Knowledge Check
The moment of inertia of semicircular ring about its centre is
AMR2BMR22CMR24DNone of theseThe moment of inertia of a uniform semicircular disc of mass M and radius r about a line perpendicular to the plane of the disc through the center is
A12Mr2BMt2C25Mr2D14Mr2The moment of inertias of a unifrom semicircular wire of mss M and radius r about a line perpendicular to the plane of the wire thorugh tehcentre is
AMr2B12Mr2C14Mr2D25Mr2
From a circular disc of radius R and mass 9M, a small disc of radius R/3 is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is

View SolutionFrom a circular disc of radius R and mass 9 M , a small disc of mass M and radius R3 is removed concentrically . The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through its centre is
View SolutionForm a circular disc of radius R and mass 9M , a small disc of mass M and radius R/3 is removed concentrically . The moment of inertia of the remaining disc about an axis perpendicular to the the plane of the disc and passing its centre is :-
View SolutionA disc of mass m and radius R has a concentric hole of radius r. Its moment of inertia about an axis through its center and perpendicular to its plane is
View SolutionFrom a circular disc of radius R and 9M , a small disc of mass M and radius R3 is removed concentrically .The moment of inertia of the remaining disc about and axis perpendicular to the plane of the disc and passing through its centre is
View Solution
