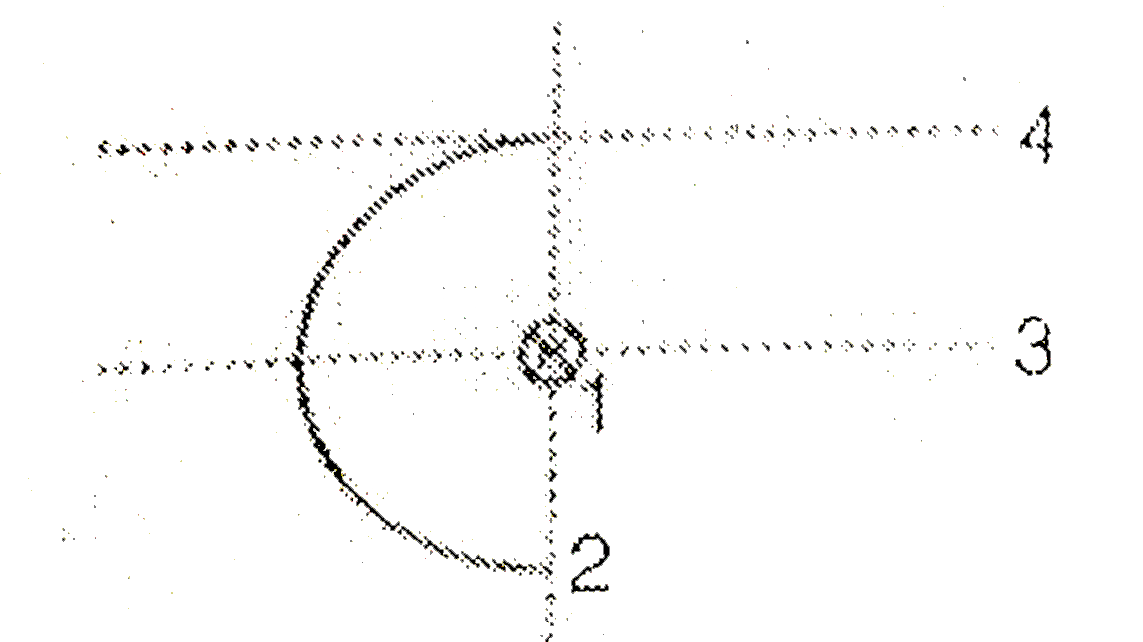
A semicircular ring has mass m and radius R as shown in figure. Let I1,I2,I3andI4 be the moments of inertia of the four axes as shown. Axis 1 passes through centre and is perpendicular to plane of ring. Then, match the following columns.

Column-IColumn-II(A)I1(p)mR22(B)I2(q)(3/2)mR2(C)I3(r)mR2(D)I4(s)Data is insufficient
The correct Answer is:(A→r,B→p,C→p,D→q)
Moment of inertia of a ring about an axis perpendicular and passing through the centre of ring is MR2. Moment of inertia of a ring about diameter is MR2/2. From parallel axes theorem,
I4=MR22+MR2=32MR2.
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (A) Chapter Exercises
83 Videos
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - Integer type q.
15 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
A semi-circular ring has mass m and radius R as shown in figure. Let I1,I2,I3 and I4 be the moments of inertia about the four axes as shown . Axis 1 passes through centre and is perpendicular to plane of ring. Then , match the following.

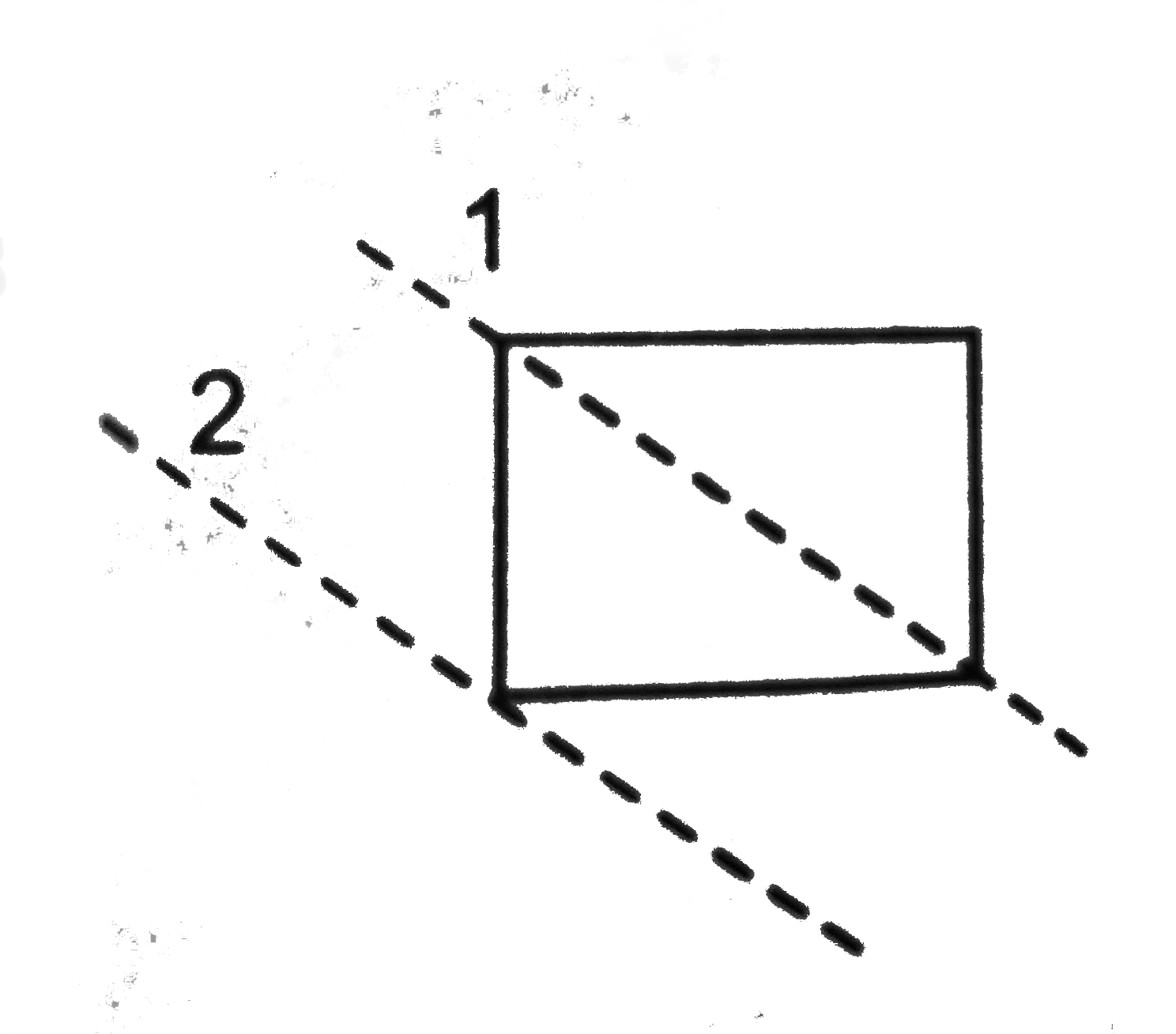
View SolutionFour rods of equal length l and mass m each forms a square as shown in figure
Moment of inertia about three axes 1,2 and 3 are say I1,I2andI3. Then, match the following columns

Column-IColumn-II(A)I1(p)43ml2(B)I2(q)23ml2(C)I3(r)12ml2(s)None
View Solution
Knowledge Check
Let I1 and I2 be the moment of inertia of a uniform square plate about axes shown in the figure. Then the ratio I1:I2 isA1:17B1:127C1:712D1:7Consider a semicircular ring with mass m and radius R as shown in figure.
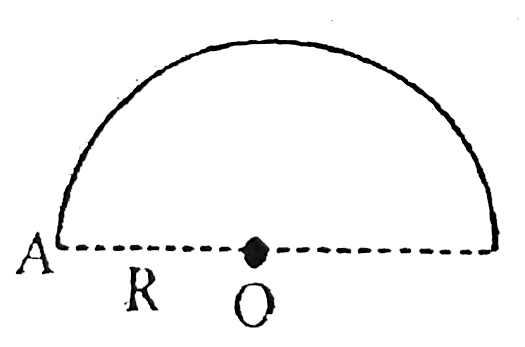
Statement-1: The moment of inertia of semi - circular ring about an axis passing through A and perpendicular to plane is 2mR2
Statement-2: According to parallel axis theorem: IA=1cm+mR2AStatement-1 is true, statement-2 is true and statement-2 is correct explanation for statement-1.BStatement-1 is true, statement-2 is true and statement-2 is NOT the correct explanation for statement-1.CStatement-1 is true, statement-2 is false.DStatement -1 is false, statement -2 is true.Let IA and IB be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of mass of the body but B does not
AIA<IBBIf IA<IB the axes are parallelCIf the axes are parallel IA<IBDIf the axes are not parallel the IA>IB
Match the species in Column I with the type of hybrid orbitals in Column II.
Column IColumn II(i)BF3(a)sp3d(ii)H2O(b)sp2(iii)PCl5(c)sp3d2(iv)SF6(d)sp3
View SolutionCalculate the values of currents ·I1I2I3andI4 Is and loin the section of networks shown in the figure

View SolutionLet IA and IB be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of mass of the body but B does not
View SolutionIf I1,I2 and I3 are the moments of inertia about the natural axies of solid sphere, hollow sphere and a spherical shell of same mass and radii, the correct result of the following is
View SolutionA ring and a thin hollow cylinder have the same mass and radius. If Ir and Is represent their moment of inertia about their axes, then
View Solution
