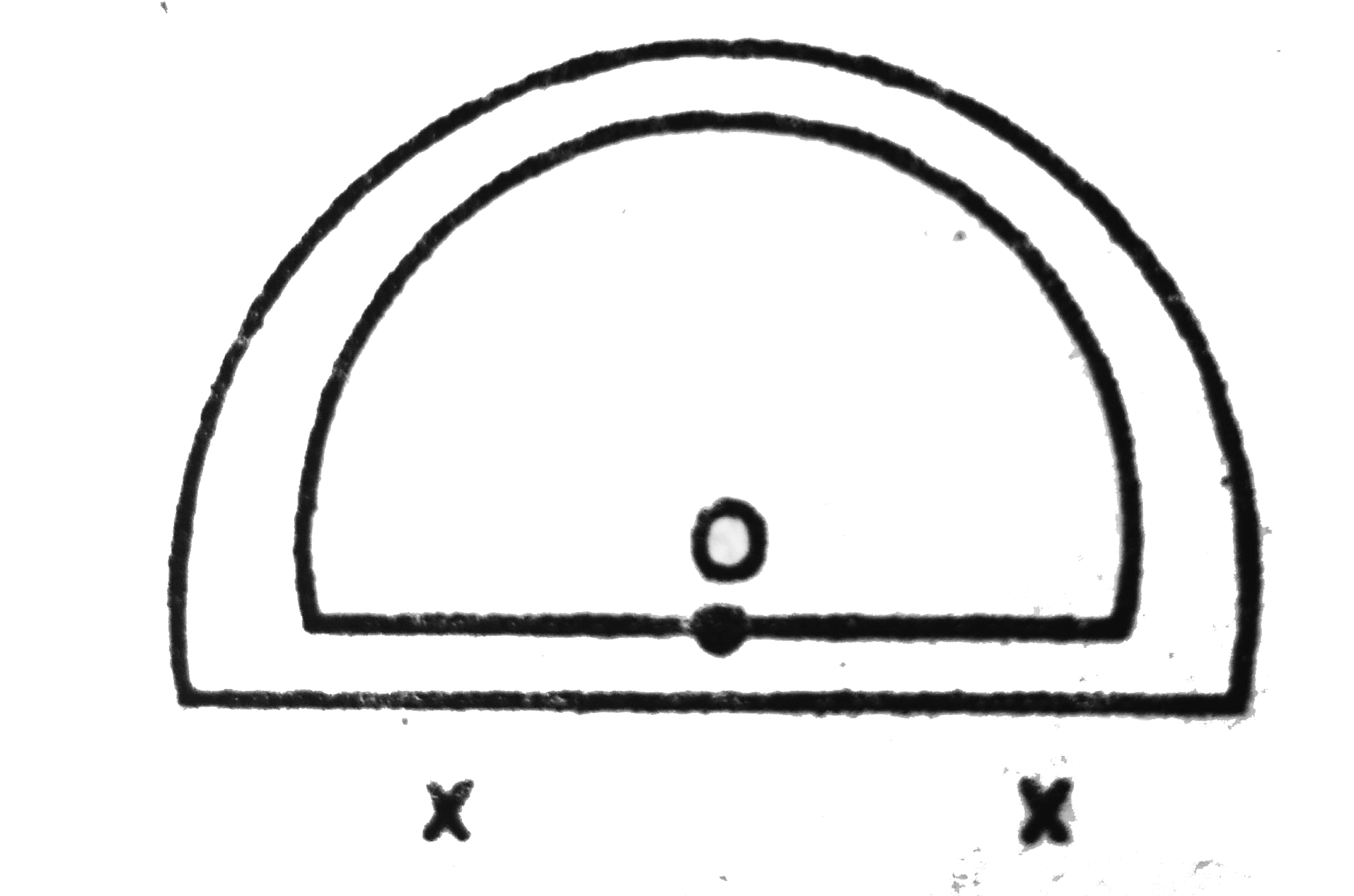
A semicircular rods is joined at its end to a straight rod of the same material and the same cross-sectional area. The straight rod formss a diameter of the other rod. The junction are maintaine dat different temperature. Find the ratio of the heat transffered through a cross section of the straigh rod in a given time.
The correct Answer is:B
We know
where
Topper's Solved these Questions
- HEAT TRANSFERBOOK - HC VERMACHAPTER - HEAT TRANSFEREXERCISE - EXERCIESE
1 Videos
- HEAT TRANSFERBOOK - HC VERMACHAPTER - HEAT TRANSFEREXERCISE - Objective 2
6 Videos
- HEAT AND TEMPERATUREBOOK - HC VERMACHAPTER - HEAT AND TEMPERATUREEXERCISE - Exercise
4 Videos
- INTRODUCTION TO PHYSICSBOOK - HC VERMACHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Exercises
19 Videos
Similar Questions
(a) Three rod of lengths 20cm each and area of cross-section 1cm2 are joined to form a triangle ABC. The conductivities of the rods are KAB=50J/m−s−.∘C,KBC=200J/m−s−.∘C and KAC=400J/m−s−.∘C. The junctions A,B and C are maintained at 40∘C, 80∘C and 80∘C respectively. Find the rate of heat flowing through the rods AB,AC and BC.
(b) A semicircular rod is joineted as its end to a straight rod of the same material and the same cross-sectional area. The straight rod forms a diameter of the other rod. The junctions are maintained at different temperatures. Find the ratio of the heat transferred through a cross-section of the simicircular rod to the heat transferred through a cross-section of the straight rod in a given time.
View SolutionThree rods of same material and of equal cross sectional area and length have been connected together as shown in the figure. The temperature of the junction of the rods approximately is
View Solution
Knowledge Check
Two rods (one semi-circular and other straight) of same material and of same cross-sectional area are joined as shown in the figure. The point A and B are maintained at different temperature. Find the ratio of the heat transferred through a cross-section of a semi-circular rod to the heat transferred through a cross section of the straight rod in a given time.
 A2πB1πCπDπ2
A2πB1πCπDπ2Two rods of different materials having differnet lengths and same cross sectional areas are joined end to end in a straight line. The free ends of this compound rod are maintained at different temperatures The temperature gradient in each rod will be .
AsameBzeroCdirectly proportional to thermal conductivity of rodDinversely proportional to thermal conductivity of the rod .Two rods are connected as shown. The rods are of same length and same cross sectional area. In steady state, the temperature (θ) of the interface will be -
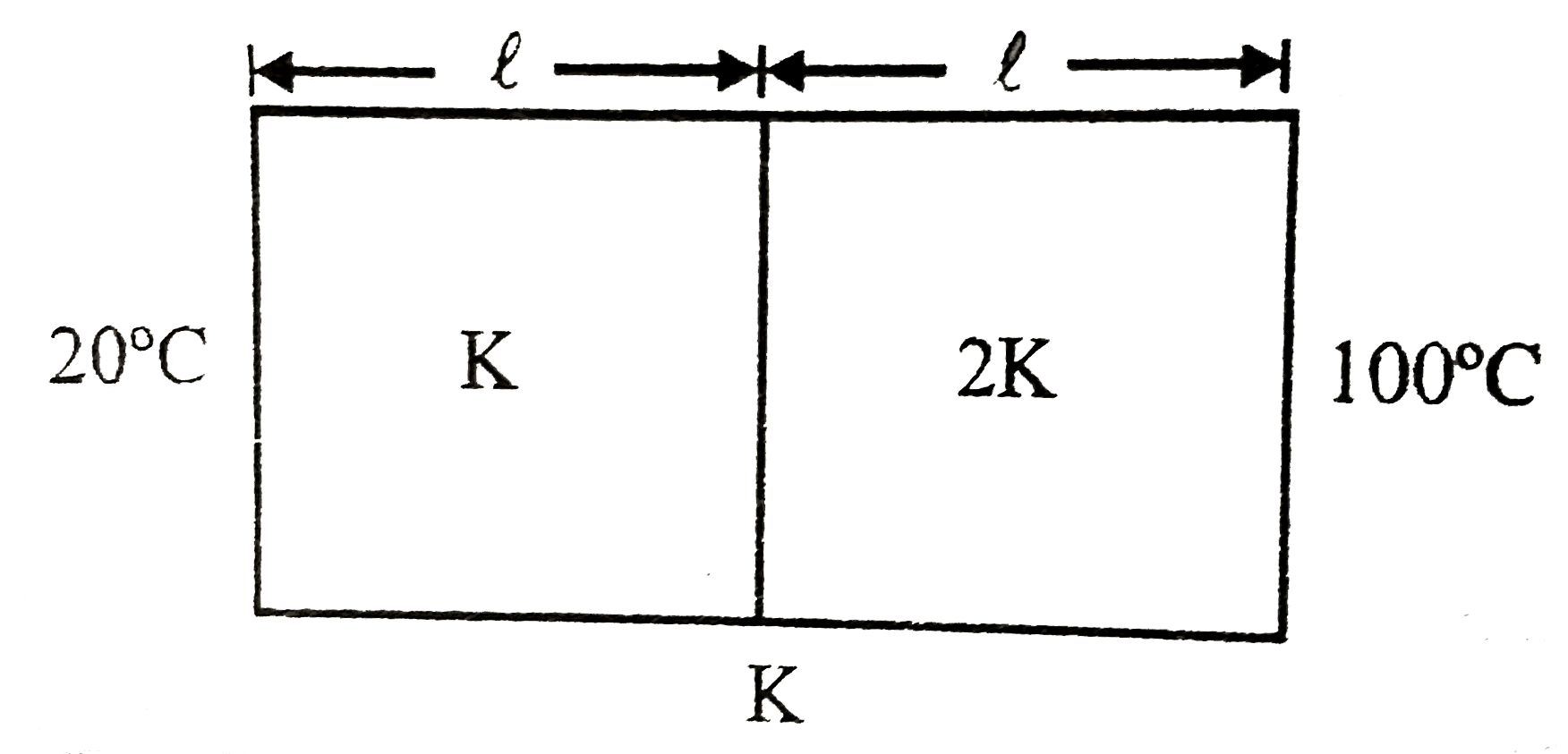 A60∘CB73.3∘CC46.7∘CD37.3∘C
A60∘CB73.3∘CC46.7∘CD37.3∘C
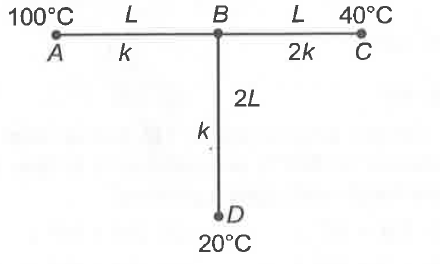
Find the temperature of junction at B, if each rod has equal area of cross-section.
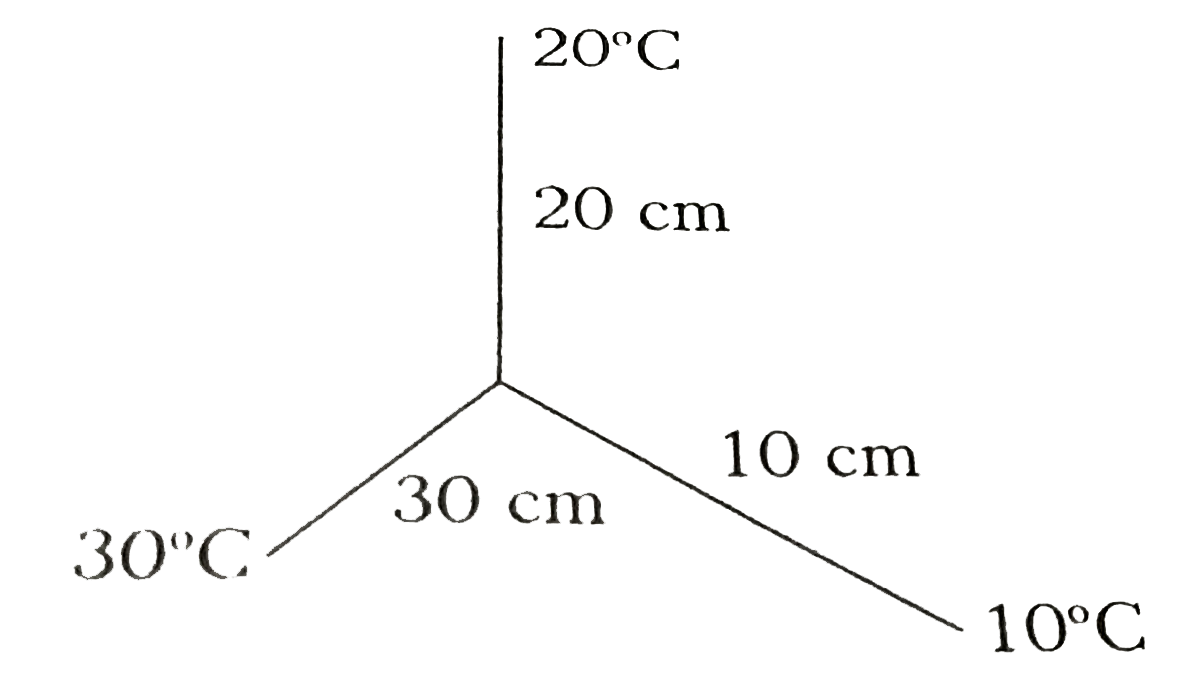
View SolutionThree rods made of the same material and having same cross-section area but different length 10 cm, 20 cm and 30 cm are joined as shown. The temperature of the junction is
View SolutionThe ends of the two rods of different materials with their lengths, diameters of cross-section and thermal conductivities all in the ratio 1 : 2 are maintained at the same temperature difference. The rate of flow of heat in the shorter rod is 1cals−1. What is the rate of flow of heat in the larger rod:
View SolutionThree rods made of same material and having the same cross-section have been joined as shown. In the figure.Each rod is of the same length. The left and right ends are kept at 0∘Cand90∘C respectively. The temperature of the junction of the three rods will be
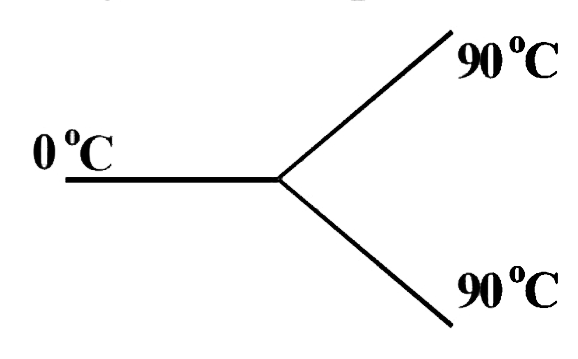
View SolutionThree rods are made from the same material and having the same cross-sectional area and length have been joined as shown in the figure.
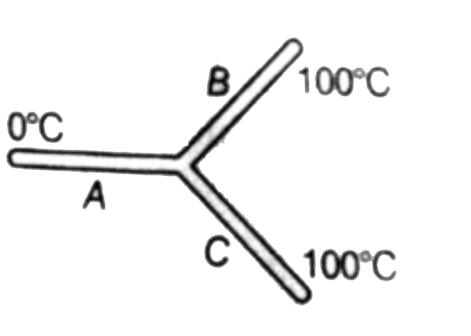
The left end and right end are kept 0∘Cand100∘C , respectively . The temperature of the junction of three rods will be
View Solution
