A series resonant LCR circuit has a quality factor (Q-factor)=0.4. If R=2kΩ,C=0.1μF then the value of inductance is
0.1H
0.064H
2 H
5 H
The correct Answer is:B
To find the value of inductance L in a series resonant LCR circuit with a given quality factor Q, resistance R, and capacitance C, we can follow these steps:
1. Identify the given values:
- Quality factor Q=0.4
- Resistance R=2kΩ=2000Ω
- Capacitance C=0.1μF=0.1×10−6F
2. Use the formula for the quality factor Q:
The quality factor for a series resonant circuit is given by the formula:
Q=1R√LC
3. Rearrange the formula to solve for L:
First, we can rearrange the equation:
Q⋅R=√LC
Now, squaring both sides gives:
(Q⋅R)2=LC
Therefore, we can express L as:
L=(Q⋅R)2⋅C
4. Substitute the known values into the equation:
L=(0.4⋅2000)2⋅(0.1×10−6)
5. Calculate Q⋅R:
Q⋅R=0.4⋅2000=800
6. Square the result:
(Q⋅R)2=8002=640000
7. Multiply by C:
L=640000⋅(0.1×10−6)=640000⋅0.0000001=0.064H
8. Convert to milliHenries:
L=0.064H=64mH=6.4mH
Final Answer:
The value of inductance L is 0.064H or 6.4mH.
- Quality factor Q=0.4
- Resistance R=2kΩ=2000Ω
- Capacitance C=0.1μF=0.1×10−6F
The quality factor for a series resonant circuit is given by the formula:
Q=1R√LC
First, we can rearrange the equation:
Q⋅R=√LC
Now, squaring both sides gives:
(Q⋅R)2=LC
Therefore, we can express L as:
L=(Q⋅R)2⋅C
L=(0.4⋅2000)2⋅(0.1×10−6)
Q⋅R=0.4⋅2000=800
(Q⋅R)2=8002=640000
L=640000⋅(0.1×10−6)=640000⋅0.0000001=0.064H
L=0.064H=64mH=6.4mH
The value of inductance L is 0.064H or 6.4mH.
Topper's Solved these Questions
Similar Questions
In a series resonant L-C-R circuit, the capacitance is changed from C to 3C. For the same resonant frequency, the inductance should be changed from L to
View SolutionIn a series LCR circuit, at resonance, power factor is …….. .
View SolutionA : A series resonant circuit is also known as an acceptor circuit.
R : For large value of Ohmic resistance, the quality factor of a series resonant circuit is high.
View SolutionA : The chief characteristic of series resonant circuit is voltage magnification.
R : At resonance the voltage drop across inductance (or capacitance) is Q times the applied voltage.
View SolutionIn a series resonant LCR circuit the voltage across R is 100 volts and R = 1k(Ω)withC=2(μ)F. The resonant frequency (ω) is 200rad/s. At resonance the voltage across L is
View SolutionAnswer the following:
(a) What do you understand by 'sharpness of resonance' for a series LCR resonant circuit? How is it related with the quality factor 'Q' of the circuit? Using the graphs given in the diagram, explain the factors which affect it. For which graph is the resistance (R ) minimum?
(b) A 2μF capacitor, 100Ω resistor and 8H inductor are connected in series with an ac source. Find the frequency of the ac source for which the current drawn in the circuit is maximum.
If the peak value of emf of the source is 200 V, calculate the (i) maximum current, and (ii) inductive and capacitive reactance of the circuit at resonance.
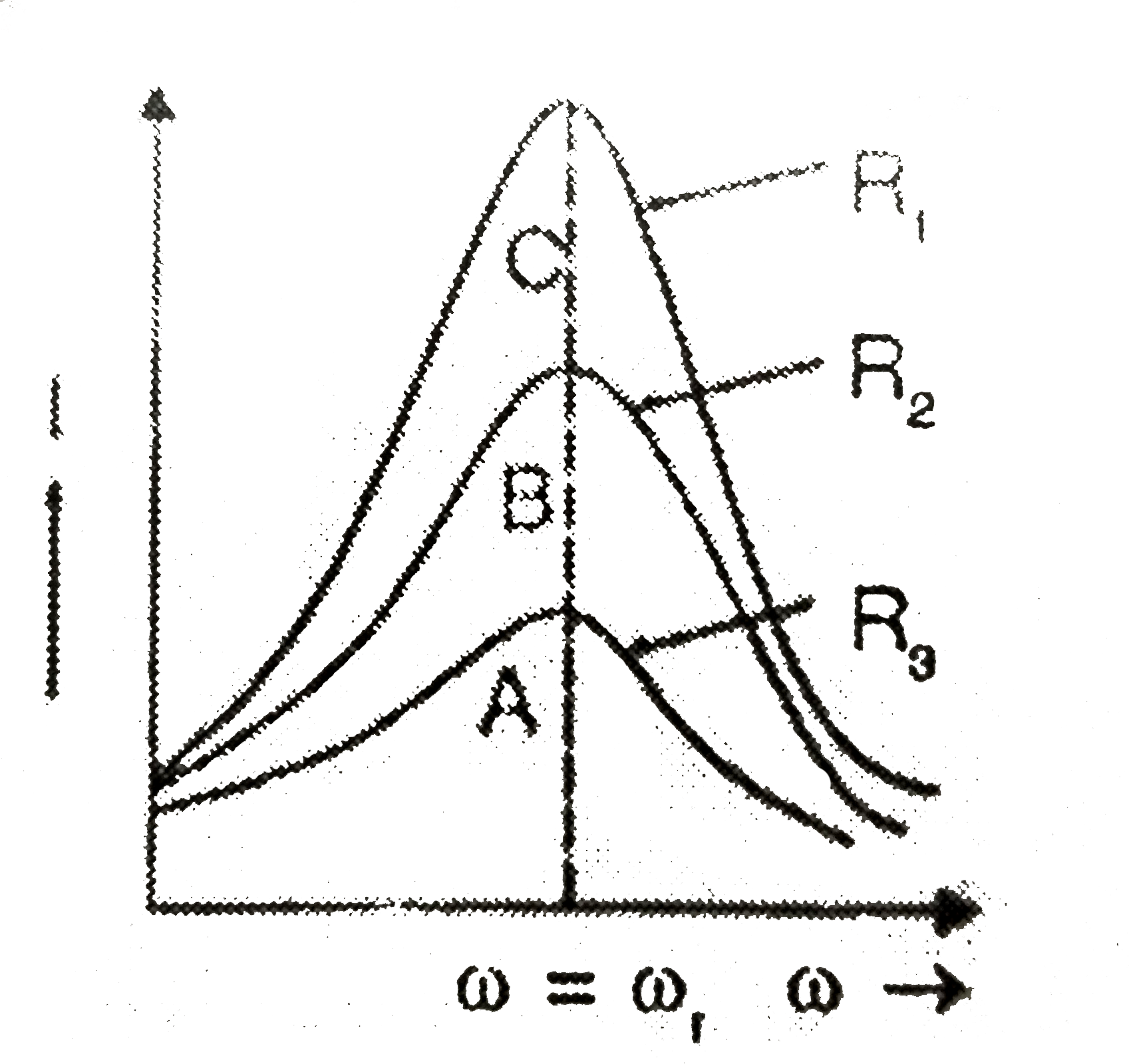
View SolutionPower factor in a series R-L-C resonant circuit is
View SolutionThe series and parallel circuits shown in figure have the same impedance and the same power factor. If R=3ΩandX=4Ω, find the values of R1andX1. Also, find the impedance and power factor.
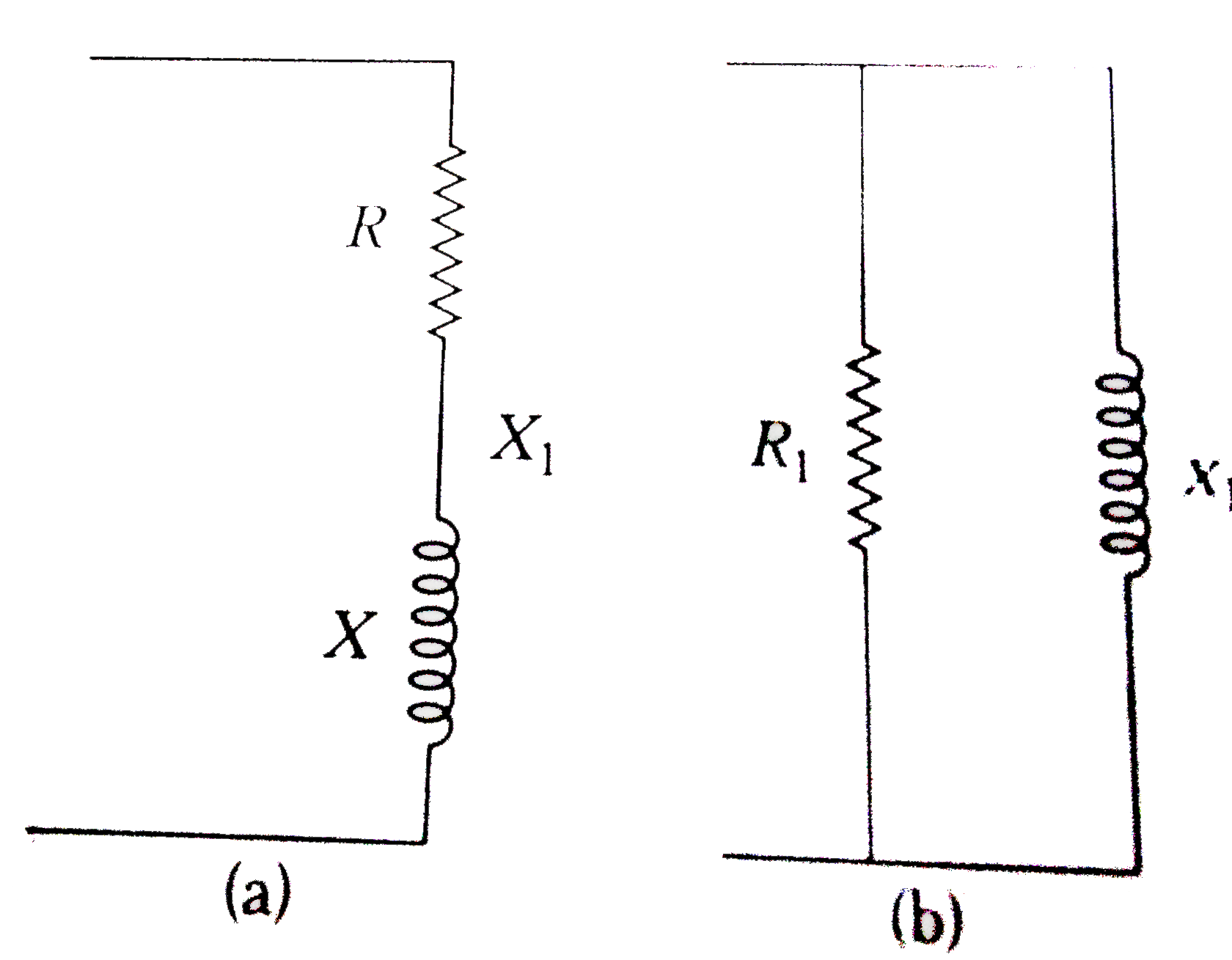
View SolutionIn a series LCR circuit with an AC source (Erms50Vandv=50/πHz),R=300Ω,C=0.02mF,L=1.0H , which of the following is correct
View SolutionThe RMS voltage of 10v is applied to a series LCR circuit having R=10ohm,L=1mH and C=10μF. Calculate the current at resonance and Q -value of the circuit at resonance.
View Solution
