A simple pendulum is constructed by attaching a bob of mass m to a string of length L fixed at its upper end. The bob oscillates in a vertical circle. It is found that the speed of the bob is v when the string makes an angle α with the vertical. Find the tension in the string and the magnitude of net force on the bob at that instant.
a. The forces acting on the bob are
i. the tension T
ii. The weight mg
As the bob moves in a circls of radius L with center at O,A centripetal force of magnitude mv2/L is required toward o.
This force will be provided by the resitant of T and mgcosα
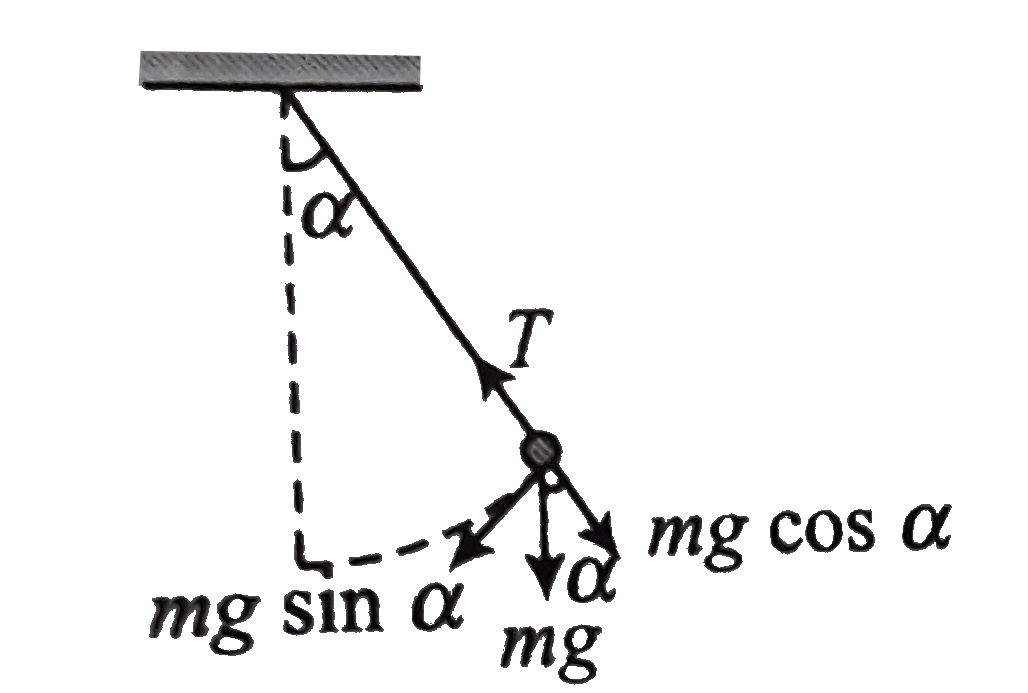
Thus T−mgcosθ=mv2L
T=m(gcosα+v2L)
ii. anet=√a21+a21=√(g2sinα)2+(v2l)2
∣∣¯¯¯Fnet∣∣=manet=m√g2sin2α+v4L2
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Subjective
21 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Single Correct
87 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.2
16 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A simple pendulum is constructed by attaching a bob of mass m to a string of length L fixed at its upper end. The bob oscillates in a vertical circle. It is found that the speed of the bob is v when the string makes an angle θ with the vertical. Find the tension in the string at this instant.
View SolutionA simple pendulum is constructed by attaching a bob of mas m to a string of length L fixed at its upper end. The bob oscillates in a vertical circle. It is found that the speed of the bob is v when the string makes an angle θ with the vertical. Find the tension in the string at this instant.
View SolutionA simple pendulum is released from rest with the string in horizontal position. The vertical component of the velocity of the bob becomes maximum, when the string makes an angle θ with the vertical. The angle θ is equal to
View SolutionA pendulum bob of mass m charge q is at rest with its string making an angle θ with the vertical in a uniform horizontal electric field E. The tension in the string in
View SolutionLet θ denote the angular displacement of a simple pendulum oscillating in a vertical plane. If the mass of the bob is m, the tension in the string is mgcosθ
View SolutionA bob of mass m attached to an inextensible string of length I is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed ω red/s about the vertical. About the point of suspension:
View SolutionThe string of a pendulum is horizontal. The mass of the bob is m. Now the string is released. The tension in the string in the lowest position is -
View SolutionA bob of mass 1 kg is suspended from an inextensible string of length 1 m. When the string makes an angle 60∘ with vertical, speed of the bob is 4 m/s
Net acceleration of the bob at this instant is
View SolutionA pendulum bob of mass m hangs from one end of a horizontal rod which is rotating about vertical axis with an unknown angular speed ω such that the light inextensible string of length l of the pedulum makes a constant angle θ with vertical. Find the
Q. tension in the string
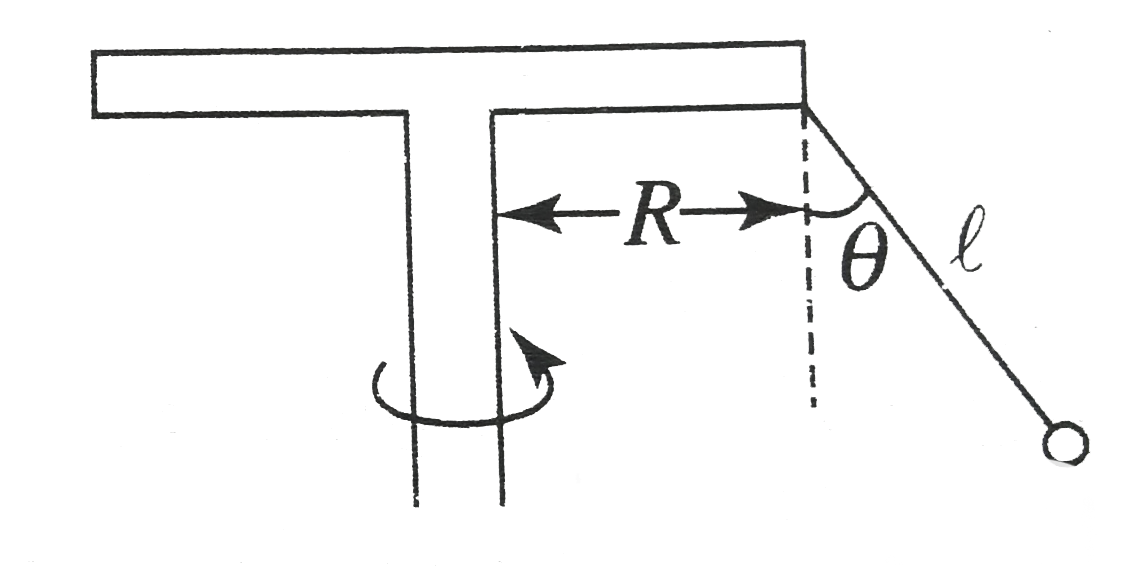
View SolutionThe bob of a 0.2 m pendulum describs an arc of circle in a vertical plane. If the tension in the cord is √3 times the weight of the bob when the cord makes an angle 30∘ with the vertical, the acceleration of the bob in that position is g/n. Find value of n.
View Solution
