Question

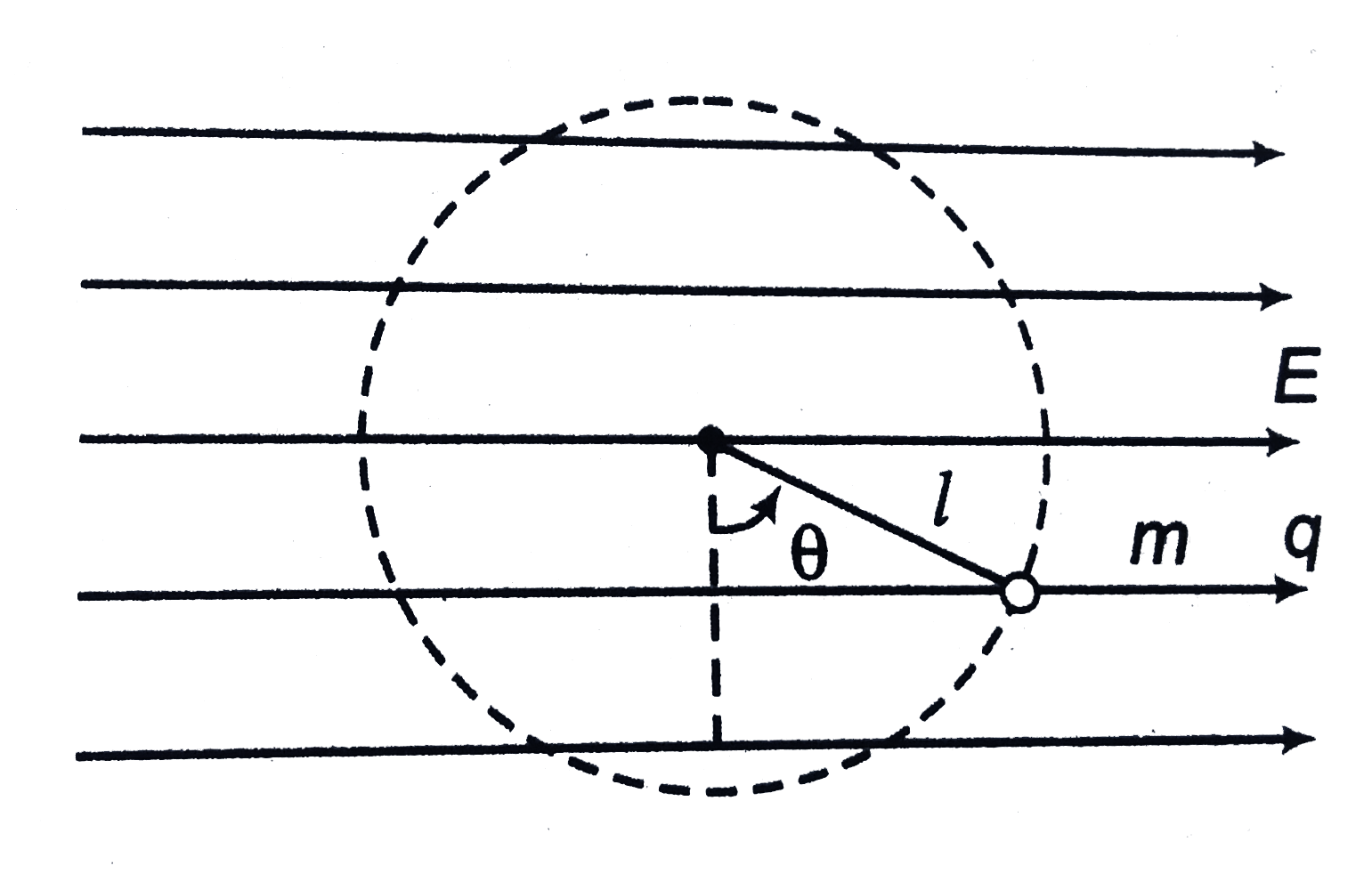
A pendulum bob of mass m charge q is at rest with its string making an angle $\theta$ with the vertical in a uniform horizontal electric field E. The tension in the string in

Options

A. `(mg)/(sintheta)`
B. `mg`
C. `(qE)/(sintheta)`
D. `(qE)/(costheta)`

Answer

C

Explanation

To find the tension in the string of a pendulum bob of mass $$m$$ and charge $$q$$ that is at rest while making an angle $$\theta$$ with the vertical in a uniform horizontal electric field $$E$$, we can follow these steps:

Step 1: Understand the Forces Acting on the Pendulum Bob
The forces acting on the pendulum bob are:
1. The weight of the bob, \( mg \), acting vertically downward.
2. The tension in the string, \( T \), acting along the string.
3. The electrostatic force due to the electric field, \( F_E = qE \), acting horizontally in the direction of the electric field.

Step 2: Resolve the Tension into Components
The tension \( T \) can be resolved into two components:
- Vertical component: \( T \cos \theta \)
- Horizontal component: \( T \sin \theta \)

Step 3: Apply the Conditions for Equilibrium
Since the pendulum bob is at rest, it is in equilibrium. Therefore, we can set up the following equations based on the equilibrium conditions:

Vertical Equilibrium
In the vertical direction, the upward force (tension's vertical component) must balance the downward force (weight of the bob):
\( T \cos \theta = mg \tag{1} \)

Horizontal Equilibrium
In the horizontal direction, the horizontal component of tension must balance the electrostatic force:
\( T \sin \theta = qE \tag{2} \)

Step 4: Solve for Tension \( T \)
From equation (1):
\( T = \frac{mg}{\cos \theta} \tag{3} \)

From equation (2):
\( T = \frac{qE}{\sin \theta} \tag{4} \)

Step 5: Equate the Two Expressions for Tension
Since both equations (3) and (4) represent the tension \( T \), we can set them equal to each other:
\( \frac{mg}{\cos \theta} = \frac{qE}{\sin \theta} \)

Step 6: Rearranging to Find Tension
From this equation, we can express \( T \) in terms of either mass, charge, electric field, and angle:
\( T = \frac{qE}{\sin \theta} \quad \text{(from equation (4))} \)

Final Expression for Tension
Thus, the tension in the string is given by:
\( T = \frac{qE}{\sin \theta} \)

Conclusion
The correct expression for the tension in the string of the pendulum bob is:
\( T = \frac{qE}{\sin \theta} \)