A simple pendulum of length L and mass m has a spring of force constant k connected to it at a distance h below its point of suspension. Find the frequency of vibrations of the system for small values of amplitude.

Video Solution

Text Solution

Verified by Experts

The frequency of vibration should be greater than that of a simple pendulum since the spring addsan additional restoring force.
$f > \frac{1}{2 π} \sqrt{\frac{g}{l}}$

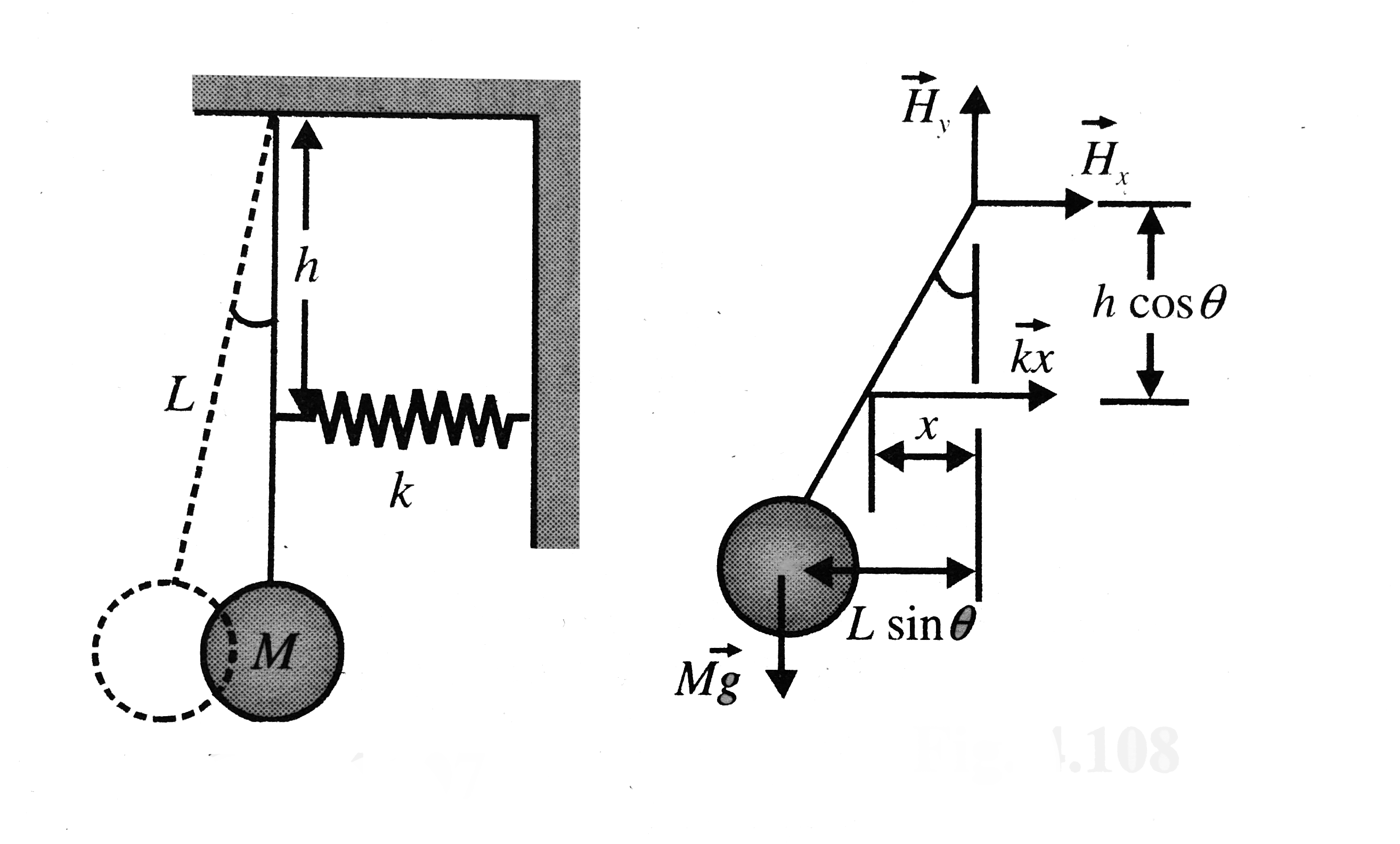
We can find the frequency $ω$ , which is found in equation for angular SHM : $d^{2} θ / {d t}^{2} = - ω^{2} θ$ . The angular acceleration can be found from analysing the tarque acting on the pendulum.
Fior the pendulum (see sketch)
$Σ τ = l α and d^{2} θ / {d t}^{2} = - α$
The negative sign appears because positive $θ$ is measured clockwise in the picture. We take torque around the point of suspension:
$Σ τ = M g L sin θ + k x h cos θ = l α$
For small amplitude vibrations, use the approximations:
$sin θ = cos θ \approx 1, and x = h tan θ = h θ$
Therefore, with $l = m L^{2}$ .
$\frac{d^{2} θ}{{d t}^{2}} = - ω^{2} θ$
With angular frequency $ω = \sqrt{\frac{M g L + k h^{2}}{M L^{2}}} = 2 π f$
The frequency is $f = \frac{ω}{2 π} = \frac{1}{2 π} \sqrt{\frac{M g L + k h^{2}}{M L^{2}}}$

Updated on:21/07/2023

Two springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is
A $\frac{1}{2 π} \sqrt{\frac{m}{k}}$
B $\frac{1}{2 π} \sqrt{2 \frac{k}{m}}$
C $\frac{1}{2 π} \sqrt{3 \frac{k}{m}}$
D $\frac{1}{2 π} \sqrt{\frac{m}{k}}$
Two springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is
A $\frac{1}{2 π} \sqrt{\frac{m}{k}}$
B $\frac{1}{2 π} \sqrt{2 \frac{k}{m}}$
C $\frac{1}{2 π} \sqrt{3 \frac{k}{m}}$
D $\frac{1}{2 π} \sqrt{\frac{m}{k}}$
A pendulam of length L and bob of mass M has a speing of force constant K connected a speing of force constsnt K connected horizontally to it at a distance h below is point of suspension. The rod is in equilibrium in vertical podition. The rod of length L. used for vertical suspension s rigid and massless. The frequency of vibration of the system for small values of $θ$ is

A $\frac{1}{2 π L} \sqrt{g L + \frac{k h}{m}}$
B $\frac{1}{2 π L} \sqrt{\frac{m g L + k}{m}}$
C $2 π \sqrt{\frac{k L^{2}}{m g L + k h}}$
D $\frac{1}{2 π L} \sqrt{g L + \frac{k h^{2}}{m}}$