A simple pendulum of length l1 has frequency 1/4 Hz and another simple pendulum of length l2 has frequency 1/3 Hz. Then time period of pendulum of length (l1−l2) is
5 s
1 s
√7s
√12s
The correct Answer is:C
n2n1=√l1l2
34=√l1l2
916=l1l2∴l2l1=169
l2−l1l1=16−99=79
√l1−l2l1=√73∴T1−T2 is √7.
Topper's Solved these Questions
Similar Questions
What is simple pendulum? Derive an expression for the time period and frequency of a simple pendulum of length I. What will be the effect on the time period of a simple pendulum if length of the pendulum becomes (a) greater than the radius of the Earth (b) becomes equal to the radius of the Earth?
View SolutionIf the period of a simple pendulum is 2s, then its frequency is 0.5Hz
View Solution
Knowledge Check
A simple pendulum of length l1 has a time period of 4 s and another simple pendulum of length l2 has a time period 3 s. Then the time period of another pendulum of length (l1−l2) is
A√3sB1sC√34sD√7sThe time period of a simple pendulum of infinte length is
AinfiniteB2π√R/gC2π√g/RD12π√R/gA simple pendulum of length 25 cm has a time period of 1 s and another pendulum of length 100cm has a time period of 2s. The time period of a simple pendulum of length 125 cm will be
A3 sB2.5 sC√5sD√7s
The l−T2 graph of a simple pendulum is an shown in the figure. The time period of the pendulum of length 0.5 mm is
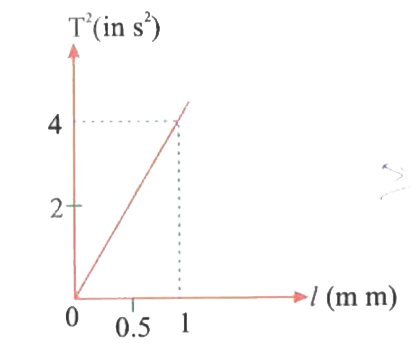
View SolutionHow does time period (T) of seconds pendulum very with length (l) ?
View SolutionThe graph of time period (T) of simple pendulum versus its length (l) is
View SolutionAn amplitue of a simple pendulum of a period 'T' and length 'L' is increased by 5%. The new period of that pendulum will be
View SolutionFor a simple pendulum, the graph between T2andL (where T is the time period & Lis the length) is
View Solution
