A skier starts from rest at point A and slides donw the hill without turning or breaking. The friction coefficient is μ When he stops at point B, his horizontal displacement is S. whalt is the height difference between points A and B?
(The velocity of the skier is small so that the additional pressure on the snow due to the curvature can vbe neglected. Neglect also the friction of air and the dependence of μ on the velocity of the skier)
h=μS
h=μS
h=2μS
h=μS2
The correct Answer is:A
To solve the problem, we need to determine the height difference h between points A and B when a skier slides down a hill under the influence of gravity and friction. The skier starts from rest and has a horizontal displacement S when he stops at point B. The coefficient of friction is μ.
1. Identify Forces Acting on the Skier:
- The gravitational force acting on the skier is mg (where m is the mass of the skier and g is the acceleration due to gravity).
- The frictional force opposing the motion is given by Ffriction=μmg.
2. Calculate Work Done by Friction:
- The work done by the frictional force as the skier moves from A to B can be expressed as:
Wfriction=Ffriction⋅d=μmg⋅S
- Here, S is the horizontal displacement.
3. Relate Work Done to Potential Energy:
- As the skier descends, the potential energy lost is converted into work done against friction. The potential energy lost when moving down a height h is given by:
PElost=mgh
- Setting the work done by friction equal to the potential energy lost gives:
mgh=μmgS
4. Cancel Common Terms:
- We can cancel mg from both sides of the equation (assuming m≠0):
h=μS
5. Conclusion:
- The height difference h between points A and B is:
h=μS
Final Answer:
The height difference between points A and B is h=μS.
- The gravitational force acting on the skier is mg (where m is the mass of the skier and g is the acceleration due to gravity).
- The frictional force opposing the motion is given by Ffriction=μmg.
- The work done by the frictional force as the skier moves from A to B can be expressed as:
Wfriction=Ffriction⋅d=μmg⋅S
- Here, S is the horizontal displacement.
- As the skier descends, the potential energy lost is converted into work done against friction. The potential energy lost when moving down a height h is given by:
PElost=mgh
- Setting the work done by friction equal to the potential energy lost gives:
mgh=μmgS
- We can cancel mg from both sides of the equation (assuming m≠0):
h=μS
- The height difference h between points A and B is:
h=μS
The height difference between points A and B is h=μS.
Topper's Solved these Questions
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(NEET)
22 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(AIIMS)
28 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved Papers 2017(AIIMS)
26 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Integer type questions
14 Videos
- SOUND WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise 19.7
4 Videos
Similar Questions

A sealed tank containing a liquid of density ρ moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B is
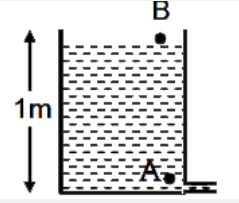
View SolutionA container of height 10 cm is filled with water. There is hole at bottom. Find the pressure difference between point A & B .
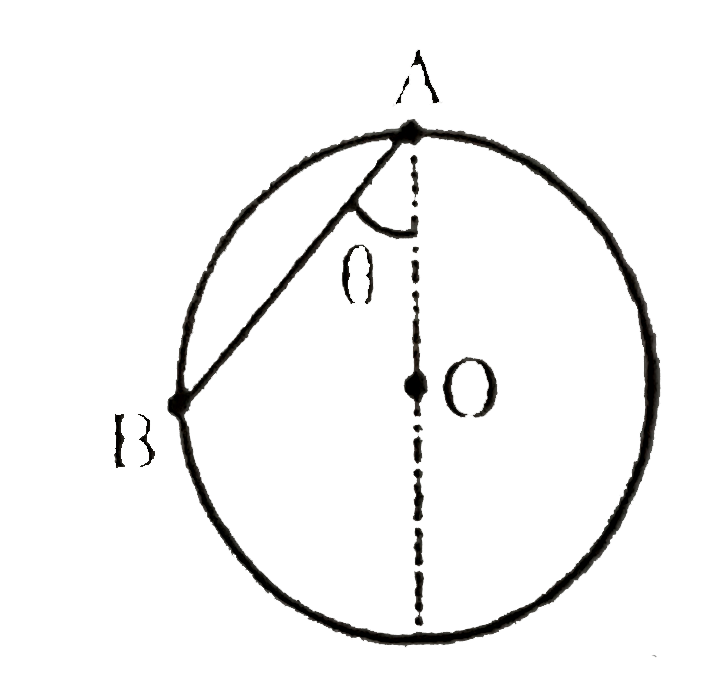
View SolutionA bead is free to slide down a smooth wire tightly stretched between points A and on a verticle circle of radius R. if the bead starts from rest at 'A', the highest point on the circle, its velocity when it arrives at B is :-
View SolutionA car starts rest, on a horizontal circular road of radius R, the tangential acceleration of the car is a. The friction coefficient between the road and the tyre is μ Find the speed at which car will skid and also find the distance after travelling it skids.
View SolutionIf the coefficient of friction between A and B is μ, the maximum acceleration of the wedge A for which B will remain at rest with respect to the wedge is
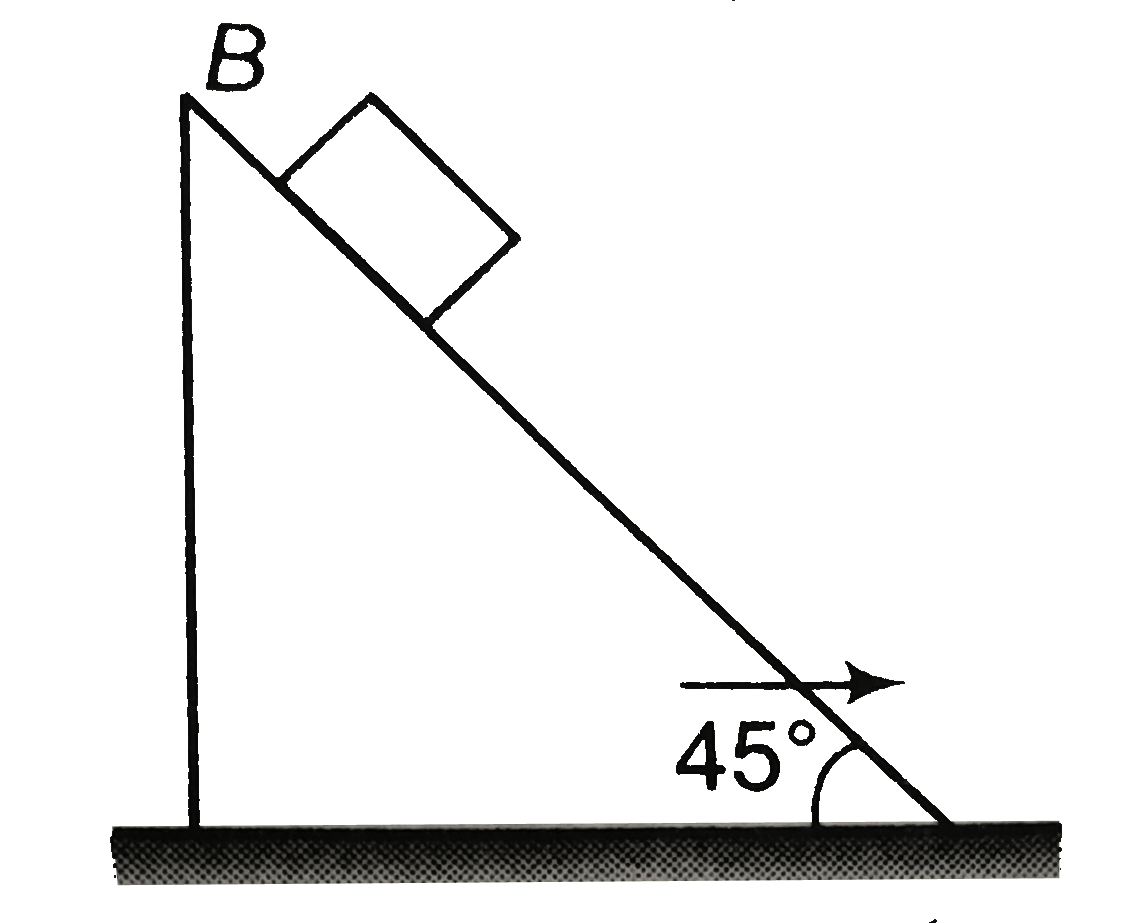
View SolutionIf the coefficient of friction between A and B is μ, the maximum acceleration of the wedge A for which B will remain at rest with respect to the wedge is

View SolutionA particle is projected directly along a rough plane of inclination θ with velocity u. If after coming to the rest the particle returns to the starting point with velocity v, the coefficient of friction between the partice and the plane is
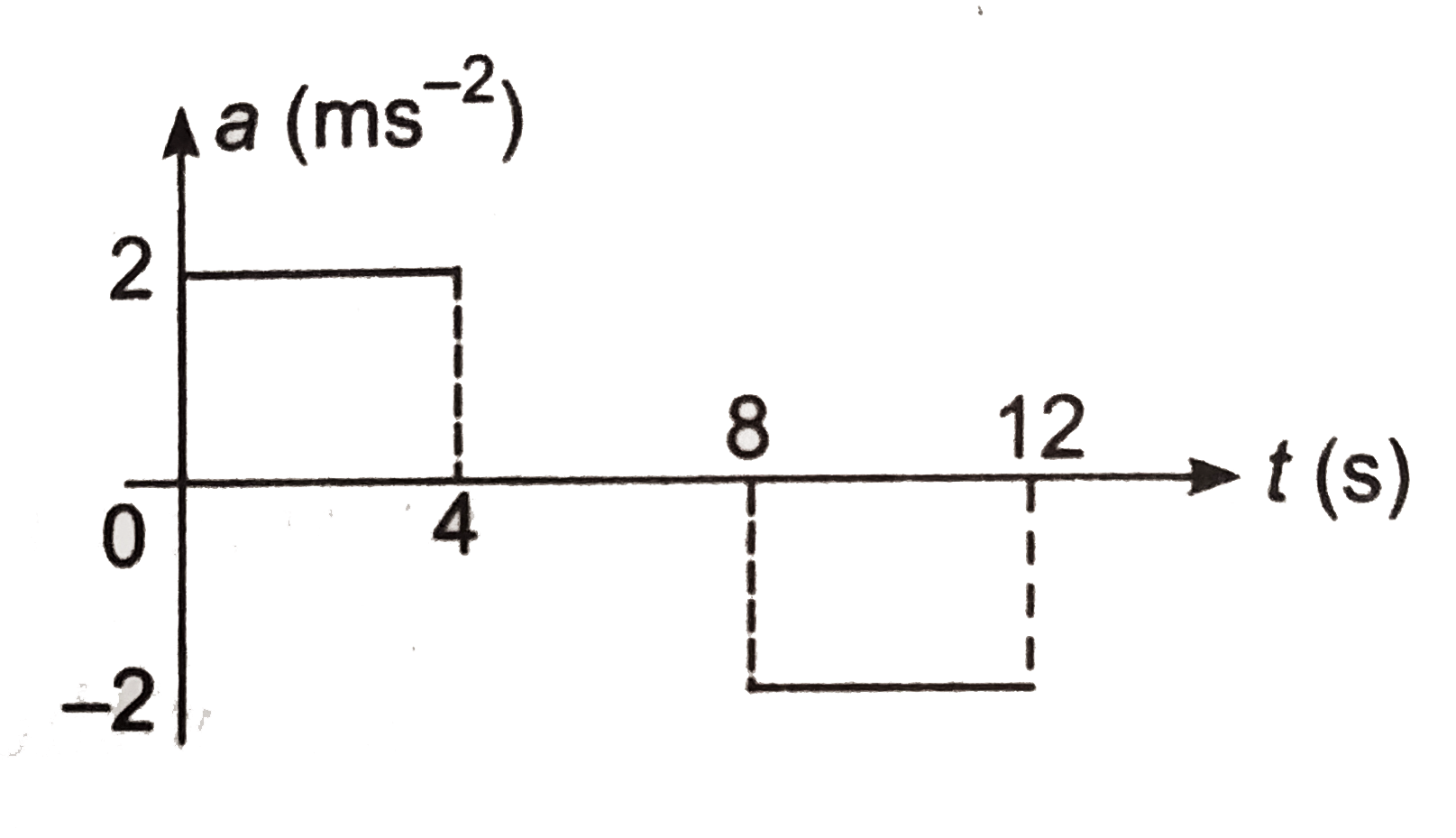
View SolutionA lift starts from rest. Its acceleration is plotted against time. When it comes to rest its height above its starting point is
View SolutionWhen a 2μC charge is carried from point A to point B, the amount of work done by the electric field is 50μJ. What is the potential difference and which point is at a higher potential ?
View SolutionA bead is free to slide down on a smooth wire rightly stretched between points AandB on a vertical circle of radius 10m. Find the time taken by the bead to reach point B, if the bead slides from rest from the highest point A on the circle.
 .
.
View Solution
