The planets with radii R1 and R2 have densities p1,p2 respectively. Their atmospheric pressues are p1 and p2 respectively.Therefore, the ratio of masses of their atmospheres, neglecting variation of g within the limits of atmoshpere is
ρ1R2p1/ρ2R1ρ2
p1R2ρ2/pP2R1ρ1
p1R1ρ1/p2R2ρ2
p1R1ρ2/p2R2ρ1
The correct Answer is:D
To solve the problem, we need to find the ratio of the masses of the atmospheres of two planets based on their given parameters. Let's break down the solution step by step.
Step 1: Understanding the relationship between gravity, density, and radius
The acceleration due to gravity g on the surface of a planet can be expressed as:
g=G⋅MR2
where G is the gravitational constant, M is the mass of the planet, and R is its radius.
The mass M of a planet can be expressed in terms of its density ρ and volume V:
M=ρ⋅V
For a spherical planet, the volume V is given by:
V=43πR3
Thus, the mass becomes:
M=ρ⋅43πR3
Step 2: Expressing gravity in terms of density and radius
Substituting the expression for mass into the formula for gravity, we get:
g=G⋅(ρ⋅43πR3)R2=43πGρR
This shows that gravity is proportional to the product of density and radius:
g∝ρR
Step 3: Finding the ratio of gravitational accelerations
For two planets with densities ρ1,ρ2 and radii R1,R2, the ratio of their gravitational accelerations g1 and g2 can be expressed as:
g1g2=ρ1R1ρ2R2
This will be our Equation (1).
Step 4: Relating atmospheric pressure to mass
The atmospheric pressure P on a planet can be expressed as:
P=WA
where W is the weight of the atmosphere and A is the surface area of the planet. The weight W can be expressed as:
W=m⋅g
Thus, we can write:
P=m⋅gA
Rearranging gives:
m=P⋅Ag
Step 5: Finding the ratio of masses of the atmospheres
For the two planets, we can express the masses of their atmospheres m1 and m2 as:
m1=P1⋅A1g1,m2=P2⋅A2g2
The surface area A of a sphere is given by A=4πR2. Therefore:
A1=4πR21,A2=4πR22
Substituting these into the mass equations:
m1=P1⋅(4πR21)g1,m2=P2⋅(4πR22)g2
Now, taking the ratio:
m1m2=P1⋅(4πR21)/g1P2⋅(4πR22)/g2
The 4π cancels out:
m1m2=P1R21g2P2R22g1
Step 6: Substituting g1 and g2
Using Equation (1) to substitute g1 and g2:
g2g1=ρ2R2ρ1R1
Thus, we can write:
g2=g1⋅ρ2R2ρ1R1
Substituting this into the mass ratio equation:
m1m2=P1R21⋅g1⋅ρ2R2ρ1R1P2R22⋅g1
The g1 cancels out:
m1m2=P1R21ρ2R2P2R22ρ1
This simplifies to:
m1m2=P1R1ρ2P2R2ρ1
Final Answer
Thus, the ratio of the masses of their atmospheres is:
m1m2=P1R1ρ2P2R2ρ1
The acceleration due to gravity g on the surface of a planet can be expressed as:
g=G⋅MR2
where G is the gravitational constant, M is the mass of the planet, and R is its radius.
M=ρ⋅V
For a spherical planet, the volume V is given by:
V=43πR3
Thus, the mass becomes:
M=ρ⋅43πR3
Substituting the expression for mass into the formula for gravity, we get:
g=G⋅(ρ⋅43πR3)R2=43πGρR
This shows that gravity is proportional to the product of density and radius:
g∝ρR
For two planets with densities ρ1,ρ2 and radii R1,R2, the ratio of their gravitational accelerations g1 and g2 can be expressed as:
g1g2=ρ1R1ρ2R2
This will be our Equation (1).
The atmospheric pressure P on a planet can be expressed as:
P=WA
where W is the weight of the atmosphere and A is the surface area of the planet. The weight W can be expressed as:
W=m⋅g
Thus, we can write:
P=m⋅gA
Rearranging gives:
m=P⋅Ag
For the two planets, we can express the masses of their atmospheres m1 and m2 as:
m1=P1⋅A1g1,m2=P2⋅A2g2
The surface area A of a sphere is given by A=4πR2. Therefore:
A1=4πR21,A2=4πR22
Substituting these into the mass equations:
m1=P1⋅(4πR21)g1,m2=P2⋅(4πR22)g2
Now, taking the ratio:
m1m2=P1⋅(4πR21)/g1P2⋅(4πR22)/g2
The 4π cancels out:
m1m2=P1R21g2P2R22g1
Using Equation (1) to substitute g1 and g2:
g2g1=ρ2R2ρ1R1
Thus, we can write:
g2=g1⋅ρ2R2ρ1R1
Substituting this into the mass ratio equation:
m1m2=P1R21⋅g1⋅ρ2R2ρ1R1P2R22⋅g1
The g1 cancels out:
m1m2=P1R21ρ2R2P2R22ρ1
This simplifies to:
m1m2=P1R1ρ2P2R2ρ1
Thus, the ratio of the masses of their atmospheres is:
m1m2=P1R1ρ2P2R2ρ1
Topper's Solved these Questions
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(NEET)
22 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(AIIMS)
28 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved Papers 2017(AIIMS)
26 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Integer type questions
14 Videos
- SOUND WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise 19.7
4 Videos
Similar Questions
Knowledge Check
The atmospheric pressure at earth surface is P1 and inside a mine is P2. They are related as :
AP1=P2BP1>P2CP1<P2DP2=0The radii of two planets are respectively R1andR2 and their densities are respectively ρ1andρ2.The ratio of the accelerations due to gravity at their surface is
AR1ρ2R2ρ1BR1ρ1R2ρ2Cρ1R22ρ2R21DR1R2ρ1ρ2
N2O4 is dissociated to 33% and 40% at total pressure P1andP2 atm respectively. Then the ratio P1/P2 is
View SolutionAssertion : In the given figure shown, p1=p2.
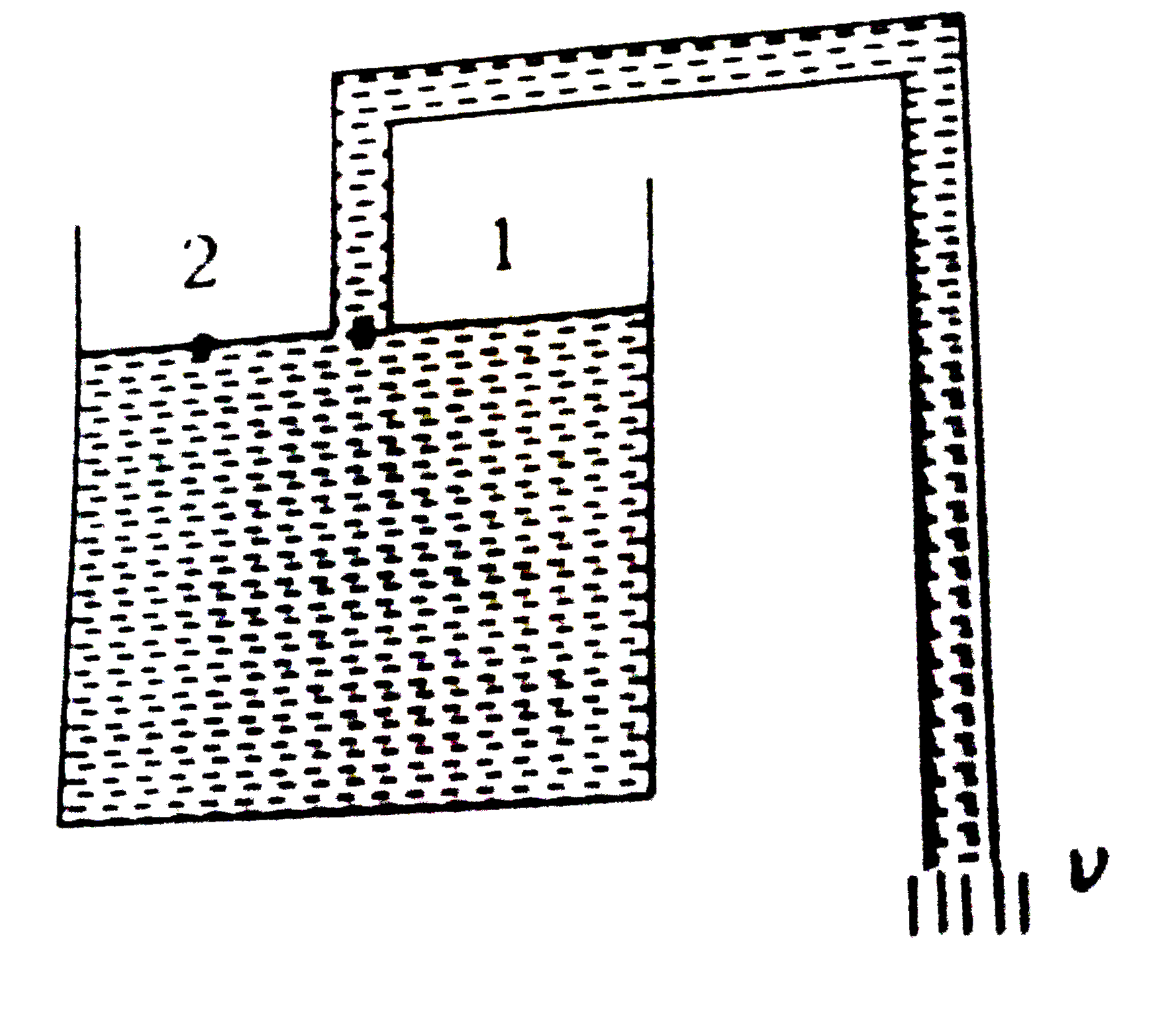
Reason : Pressure at 1 is less than the atmospheric pressure.
View SolutionIf p1,p2,p3 are respectively the perpendicular from the vertices of a triangle to the opposite sides, then find the value of p1p2p3.
View SolutionTwo concentric spherical shells of masses and radii m1,r1andm2,r2 respectively are as shown. The gravitational field intensity at point P is

View SolutionThe ratio of the radii of the planets P1andP2 is K1. the ratio of the acceleration due to gravity is K2. the ratio of the escape velocities from them will be
View SolutionTwo bodies with masses m1kgandm2kg have equal kinetic energies. If p1andP2 are their respective momenta, then p1/P2 is equal to :
View Solution