The upper half of an inclined plane with inclination ϕ is perfectly smooth while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for the lower half is given by
μ=2tanθ
μ=tanθ
μ=2/(tanθ)
μ=1/tanθ
The correct Answer is:A
To solve the problem, we need to analyze the motion of a body sliding down an inclined plane that has two different surfaces: a smooth upper half and a rough lower half.
1. Understanding the Setup:
- The inclined plane has an angle of inclination ϕ.
- The upper half of the plane is smooth (frictionless), while the lower half is rough.
2. Identifying Forces:
- When the body is at the top, it starts from rest and will slide down due to gravity.
- On the smooth surface, there is no friction, so the only force acting on the body is its weight component along the incline.
3. Calculating Work Done by Gravity:
- The work done by gravity as the body moves down the entire length of the incline (let's denote the total length as 2L) can be calculated.
- The vertical height h corresponding to the length 2L is h=2Lsinϕ.
- The work done by gravity Wg is given by:
Wg=mgh=mg(2Lsinϕ)=2mgLsinϕ
4. Calculating Work Done by Friction:
- On the rough surface, the frictional force Ff acting against the motion is given by Ff=μmgcosϕ, where μ is the coefficient of friction.
- The work done by friction Wf over the distance L (the length of the rough part) is:
Wf=−Ff⋅L=−μmgcosϕ⋅L
5. Setting Up the Equation:
- Since the body comes to rest at the bottom, the total work done on the body must equal zero (the work done by gravity must equal the work done against friction):
Wg+Wf=0
- Substituting the expressions for work done:
2mgLsinϕ−μmgcosϕ⋅L=0
6. Simplifying the Equation:
- We can cancel mgL from both sides (assuming m≠0 and L≠0):
2sinϕ−μcosϕ=0
- Rearranging gives:
μcosϕ=2sinϕ
- Therefore, we can express μ as:
μ=2sinϕcosϕ=2tanϕ
Final Answer:
The coefficient of friction for the lower half of the inclined plane is given by:
μ=2tanϕ
- The inclined plane has an angle of inclination ϕ.
- The upper half of the plane is smooth (frictionless), while the lower half is rough.
- When the body is at the top, it starts from rest and will slide down due to gravity.
- On the smooth surface, there is no friction, so the only force acting on the body is its weight component along the incline.
- The work done by gravity as the body moves down the entire length of the incline (let's denote the total length as 2L) can be calculated.
- The vertical height h corresponding to the length 2L is h=2Lsinϕ.
- The work done by gravity Wg is given by:
Wg=mgh=mg(2Lsinϕ)=2mgLsinϕ
- On the rough surface, the frictional force Ff acting against the motion is given by Ff=μmgcosϕ, where μ is the coefficient of friction.
- The work done by friction Wf over the distance L (the length of the rough part) is:
Wf=−Ff⋅L=−μmgcosϕ⋅L
- Since the body comes to rest at the bottom, the total work done on the body must equal zero (the work done by gravity must equal the work done against friction):
Wg+Wf=0
- Substituting the expressions for work done:
2mgLsinϕ−μmgcosϕ⋅L=0
- We can cancel mgL from both sides (assuming m≠0 and L≠0):
2sinϕ−μcosϕ=0
- Rearranging gives:
μcosϕ=2sinϕ
- Therefore, we can express μ as:
μ=2sinϕcosϕ=2tanϕ
The coefficient of friction for the lower half of the inclined plane is given by:
μ=2tanϕ
Topper's Solved these Questions
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(NEET)
22 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(AIIMS)
28 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved Papers 2017(AIIMS)
26 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Integer type questions
14 Videos
- SOUND WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise 19.7
4 Videos
Similar Questions
The upper half of an inclined plane with an angle of inclination theta, is smooth while the lower half is rough. A body starting from rest at the top of the inclined plane comes to rest at the bottom of the inclined plane. Then the coefficient of friction for the lower half is
View SolutionThe upper portion of an inclined plane of inclination a is smooth and the lower portion is rough. A partical slide down from rest the top and just comes to rest at the foot . If the ratio of smooth length to rough length is m:n, find the coefficient of friction .
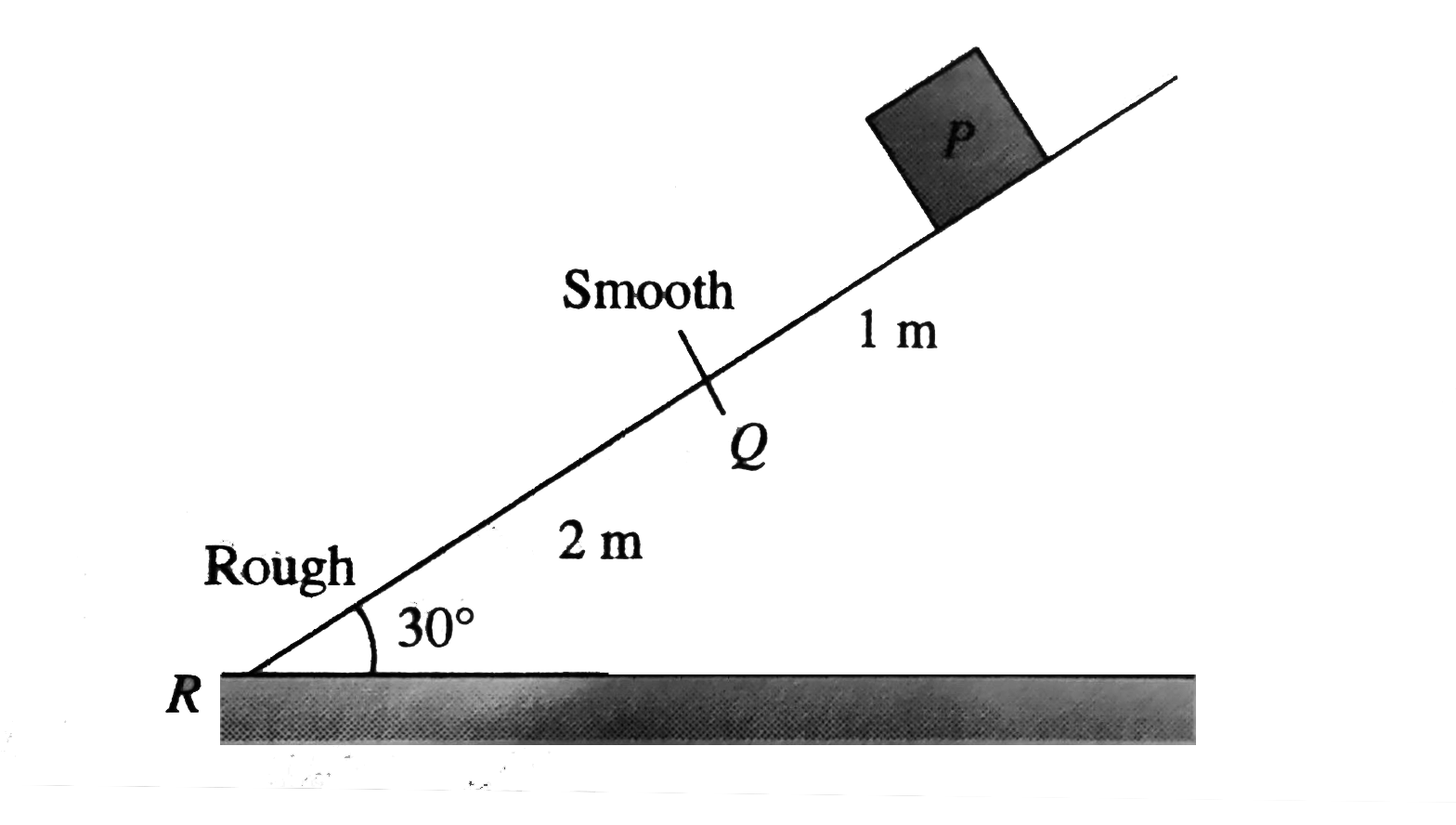
View SolutionA block of mass 5.0kg slides down from the top of an inclined plane of length 3m. The first 1m of the plane is smooth and the next 2m is rough. The block is released from rest and again comes to rest at the bottom of the plane. If the plane is inclined at 30∘ with the horizontal, find the coefficient of friction on the rough portion.
View SolutionA block of mass m is released on the top of a smooth inclined plane of length x and inclination θ as shown in figure. Horizontal surface is rough. If block comes to rest after moving a distabce d on the horizontal surface, then coefficient of friction between block and surface is :-
View SolutionA body weighing 20kg just slides down a rough inclined plane that rises 5 in 12. What is the coefficient of friction ?
View SolutionA weight w is to be moved from the bottom to the top of an inclined plane of inclination θ to the horizontal. If a smaller force is to be applied to drag it along the plane in comparison to lift it vertically up, the coefficient of friction should be such that.
View SolutionA block is at rest on an inclined plane making an angle α with the horizontal. As the angle of the incline is increased the block start slipping when the angle of inclination becomes θ then coefficient of friction is equal to
View SolutionA block is pushed up a rough inclined plane of 45°. If the time of descent is twice the time of ascent, the coefficient of friction is
View SolutionAn object is placed on the surface of a smooth inclined plane of inclination θ . It takes time t to reach the bottom of the inclined plane. If the same object is allowed to slide down rough inclined plane of same inclination θ, it takes time nt to reach the bottom where n is a number greater than 1. The coefficient of friction μ is given by -
View SolutionA body weighs 64 N on the surface of the Earth. What is the gravitational force on it (in N) due to the Earth at a height equal to one-third of the radius of the Earth?
View Solution
