A particle is projected directly along a rough plane of inclination θ with velocity u. If after coming to the rest the particle returns to the starting point with velocity v, the coefficient of friction between the partice and the plane is
u2v2tanθ
u2−v2u2+v2tanθ
v2u2tanθ
u2+v2u2−v2tanθ
The correct Answer is:B
To solve the problem, we will analyze the motion of the particle as it moves up and down the inclined plane and derive the expression for the coefficient of friction.
1. Understanding the Problem:
- A particle is projected up a rough inclined plane with an initial velocity u.
- It comes to rest and then returns to the starting point with a velocity v.
- We need to find the coefficient of friction μ between the particle and the plane.
2. Forces Acting on the Particle (Moving Up):
- When the particle moves up, the forces acting on it are:
- Gravitational force component down the incline: mgsinθ
- Normal force: N=mgcosθ
- Frictional force (acting downwards): f=μN=μmgcosθ
- The net force acting on the particle while moving up is:
Fnet=mgsinθ+μmgcosθ
- According to Newton's second law:
ma=mgsinθ+μmgcosθ
- Dividing through by m:
a=gsinθ+μgcosθ
- Since the particle is decelerating, we take a as negative:
a=−(gsinθ+μgcosθ)
3. Using Kinematics to Find Displacement (Moving Up):
- Using the kinematic equation v2=u2+2as where v=0 (final velocity when it comes to rest):
0=u2−2(gsinθ+μgcosθ)s
- Rearranging gives:
s=u22(gsinθ+μgcosθ)
4. Forces Acting on the Particle (Moving Down):
- When the particle returns down the incline, the forces are:
- Gravitational force component down the incline: mgsinθ
- Normal force: N=mgcosθ
- Frictional force (acting upwards): f=μmgcosθ
- The net force acting on the particle while moving down is:
Fnet=mgsinθ−μmgcosθ
- According to Newton's second law:
ma=mgsinθ−μmgcosθ
- Dividing through by m:
a=gsinθ−μgcosθ
5. Using Kinematics to Find Displacement (Moving Down):
- Using the kinematic equation v2=u2+2as where u=0 (initial velocity when it starts moving down):
v2=0+2(gsinθ−μgcosθ)s
- Rearranging gives:
s=v22(gsinθ−μgcosθ)
6. Equating the Two Displacements:
- Since the displacement s is the same in both cases, we can set the two expressions for s equal:
u22(gsinθ+μgcosθ)=v22(gsinθ−μgcosθ)
- Cross-multiplying gives:
u2(gsinθ−μgcosθ)=v2(gsinθ+μgcosθ)
7. Rearranging to Solve for μ:
- Expanding and rearranging:
u2gsinθ−u2μgcosθ=v2gsinθ+v2μgcosθ
- Collecting μ terms:
u2gsinθ−v2gsinθ=u2μgcosθ+v2μgcosθ
- Factoring out μ:
(u2−v2)gsinθ=μgcosθ(u2+v2)
- Finally, solving for μ:
μ=(u2−v2)sinθ(u2+v2)cosθ
Final Answer:
The coefficient of friction μ is given by:
μ=(u2−v2)tanθ(u2+v2)
- A particle is projected up a rough inclined plane with an initial velocity u.
- It comes to rest and then returns to the starting point with a velocity v.
- We need to find the coefficient of friction μ between the particle and the plane.
- When the particle moves up, the forces acting on it are:
- Gravitational force component down the incline: mgsinθ
- Normal force: N=mgcosθ
- Frictional force (acting downwards): f=μN=μmgcosθ
- The net force acting on the particle while moving up is:
Fnet=mgsinθ+μmgcosθ
- According to Newton's second law:
ma=mgsinθ+μmgcosθ
- Dividing through by m:
a=gsinθ+μgcosθ
- Since the particle is decelerating, we take a as negative:
a=−(gsinθ+μgcosθ)
- Using the kinematic equation v2=u2+2as where v=0 (final velocity when it comes to rest):
0=u2−2(gsinθ+μgcosθ)s
- Rearranging gives:
s=u22(gsinθ+μgcosθ)
- When the particle returns down the incline, the forces are:
- Gravitational force component down the incline: mgsinθ
- Normal force: N=mgcosθ
- Frictional force (acting upwards): f=μmgcosθ
- The net force acting on the particle while moving down is:
Fnet=mgsinθ−μmgcosθ
- According to Newton's second law:
ma=mgsinθ−μmgcosθ
- Dividing through by m:
a=gsinθ−μgcosθ
- Using the kinematic equation v2=u2+2as where u=0 (initial velocity when it starts moving down):
v2=0+2(gsinθ−μgcosθ)s
- Rearranging gives:
s=v22(gsinθ−μgcosθ)
- Since the displacement s is the same in both cases, we can set the two expressions for s equal:
u22(gsinθ+μgcosθ)=v22(gsinθ−μgcosθ)
- Cross-multiplying gives:
u2(gsinθ−μgcosθ)=v2(gsinθ+μgcosθ)
- Expanding and rearranging:
u2gsinθ−u2μgcosθ=v2gsinθ+v2μgcosθ
- Collecting μ terms:
u2gsinθ−v2gsinθ=u2μgcosθ+v2μgcosθ
- Factoring out μ:
(u2−v2)gsinθ=μgcosθ(u2+v2)
- Finally, solving for μ:
μ=(u2−v2)sinθ(u2+v2)cosθ
The coefficient of friction μ is given by:
μ=(u2−v2)tanθ(u2+v2)
Similar Questions
A particle is projected on a frictionless inclined plane of inclination 37∘ at an angle of projection 45∘ from the inclined plane as shown in the figure. If after the first collision from the plane, the particle returns to its point of projection, then what is the value of the reciprocal of the coefficient of restitution between the particle and the plane?
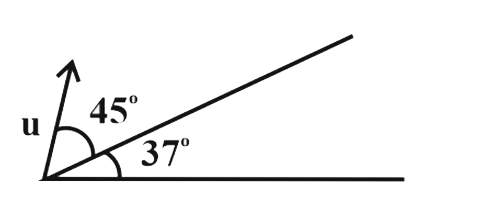 View Solution
View SolutionA particle is projected up a 45∘ rough incline with a velocity v. The coeffciient of friciton is 0.5. The speed with which it returns back to the starting point is v'. Then v' /v is :
View SolutionA block starts moving up an inclined plane of inclination 30∘ with an initial velocity of v0 . It comes back to its initial position with velocity v02 . The value of the coefficient of kinetic friction between the block and the inclined plane is close to I1000 , The nearest integer to I is ____________ .
View SolutionA block is placed on a rough inclined plane of inclination θ=30∘. If the force to drag it along the plane is to be smaller than to lift it. The coefficient of friction μ should be less than
View SolutionA positively charged particle of mass m and charge q is projected on a rough horizontal x-y plane surface with z-axis in the vertically upward direction. Both electric and magnetic fields are acting in the region and given by →E=−E0ˆkand→B=−B0ˆk , respectively. The particle enters into the field at (a0,0,0) with velocity →v=v0ˆj. The particle starts moving in some curved path on the plane. If the coefficient of friction between the particle and the plane is μ. Then calculate the
(a) time when the particle will come to rest
(b) distance travelled by the particle when it comes to rest.
 View Solution
View SolutionA positively charged particle of mass m and charge q is projected on a rough horizontal x-y plane surface with z-axis in the vertically upward direction. Both electric and magnetic fields are acting in the region and given by →E=−E0ˆkand→B=−B0ˆk , respectively. The particle enters into the field at (a0,0,0) with velocity →v=v0ˆj. The particle starts moving in some curved path on the plane. If the coefficient of friction between the particle and the plane is μ. Then calculate the
(a) time when the particle will come to rest
(b) distance travelled by the particle when it comes to rest.
 View Solution
View SolutionA block starts going up a rough inclined plane with velocity V0 as shown in figure.After some time reaches to starting point again, with a velocity V02.Find coefficient of friction μ .Given g=10msec2.
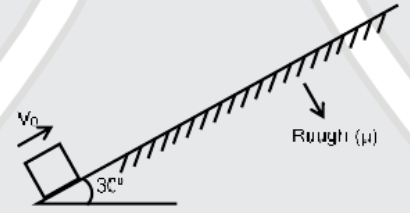 View Solution
View SolutionA particle of mass m strikes a horizontal smooth floor with velocity u making an angle θ with the floor and rebound with velocity v making an angle θ with the floor. The coefficient of restitution between the particle and the floor is e. Then
View SolutionA particle moves move on the rough horizontal ground with some initial velocity V0. If 34 of its kinetic enegry lost due to friction in time t0. The coefficient of friction between the particle and the ground is.
View SolutionA hollow sphere rolls down a rough inclined plane whose angle of inclination is θ, with horizontal. For the hollow sphere to undergo pure rolling, without slipping, the condition is [μ = coefficient of friction between the hollow sphere and inclined plane]
View Solution

