
A small asteroid is approaching a planet of mass M and radius R from a large distance. Initially its velocity (u) is along a tangent to the surface of the planet. It fall on the surface making an angle of 302 with the vertical. Calculate u.
The correct Answer is:u=√2GM3R
Step by step video, text & image solution for A small asteroid is approaching a planet of mass M and radius R from a large distance. Initially its velocity (u) is along a tangent to the surface of the planet. It fall on the surface making an angle of 30^(2) with the vertical. Calculate u. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Mass and radius of a planet are two times the value of earth. What is the value of escape velocity from the surface of this planet?
View SolutionThe earth is a homogeneous sphere of mass M and radius R. There is another spherical planet of mass M and radius R whose density changes with distance r from the centre as p=p0r. (a) Find the ratio of acceleration due to gravity on the surface of the earth and that on the surface of the planet. (b) Find p0.
View Solution
Knowledge Check
If ve is the escape velocity of a body from a planet of mass 'M' and radius 'R. Then the velocity of the satellite revolving at height 'h' from the surface of the planet will be
Ave√RR+hBve√2RR+hCve√R+hRDve√R2(R+h)The angular velocity of rotation of a planet of mass M and radius R, at which the matter start to escape from its equator is
A√2GMR3B√2GMRC√2G2MRD√2GM2RAt satellite of mass m is launched from the surface of a planet of mass M and radius R in a circular orbit at an altitude of 3R. K.E. of satellite at the time of launching is
A78GMmRB87GMmRC67GMmRD78GMmR2
A small asteroid is at a large distance from a planet and its velocity makes an angle phi(cancel(=)0) with line joining the asteroid to the centre of the planet. Prove that such an asteroid can never fall normally on the surface of the planet.

View SolutionA spaceship is sent to investigate a planet of mass M and radius R. While hanging motionless in space at a distance 5R from the centre of the planet, the spaceship fires an instrument package of mass m, which is much smaller than the mass of the spaceship. For what angle θ will the package just graze the surface of the planet?
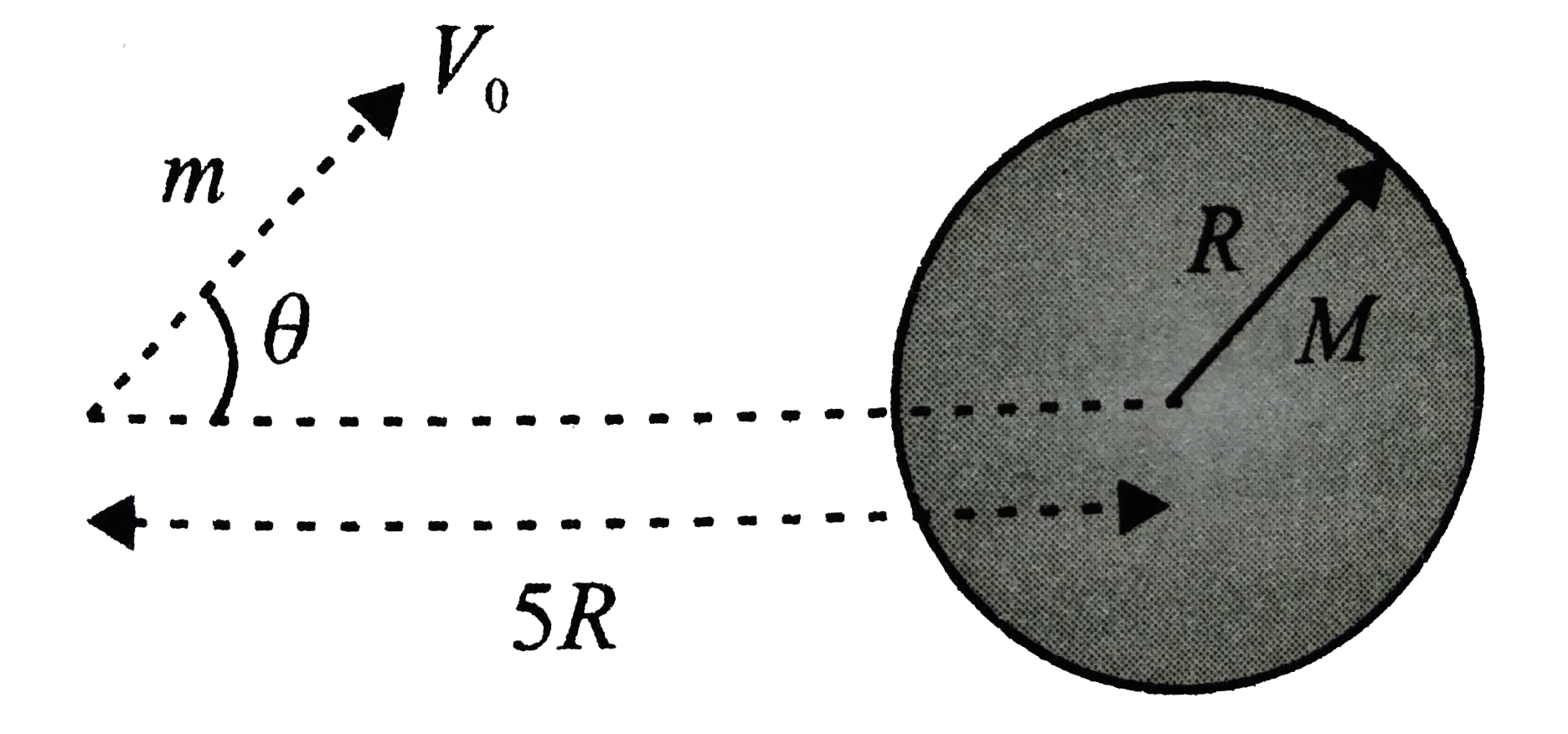
View Solution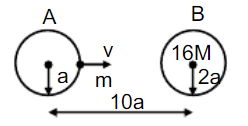
Two planets of mass M and 16M of radius a and 2a respectively, are at distance 10a. Find minimum speed of a particle of mass m at surface of smaller planet so that it can reached from smaller planet to larger planet.
View Solution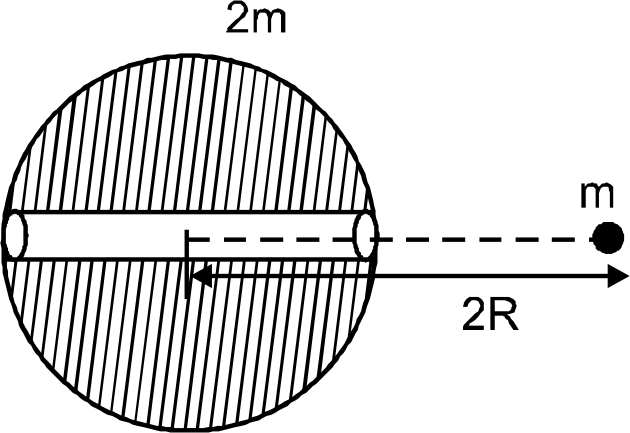
A solid spherical planet of mass 2m and radius 'R' has a very small tunnel along its diameter. A small cosmic particle of mass m is at a distance 2R from the centre of the planet as shown. Both are initially at rest, and due to gravitational attraction, both start moving toward each other. After some time, the cosmic particle passes through the centre of the planet. (Assume the planet and the cosmic particle are isolated from other planets)
View SolutionIf the radius of a planet is R and its density is ρ , the escape velocity from its surface will be
View Solution
