A small ball of density rho_(0) is released from the surface of a liquid whose density varies with depth h as ρ=ρ02(α+βh). Mass of the ball is m. Select the most appropriate one option.
The particle will execute SHM
The maximum speed of the ball is 2−α√2β
Both a and b are correct
Both a and b are wrong
The correct Answer is:A
Step by step video & image solution for A small ball of density rho_(0) is released from the surface of a liquid whose density varies with depth h as rho=(rho_(0))/2(alpha+betah). Mass of the ball is m. Select the most appropriate one option. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:More than one option is correct
Explore 50 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Comprehension types
Explore 18 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Only one question is correct
Explore 48 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBook:DC PANDEY ENGLISHChapter:SEMICONDUCTORS AND ELECTRONIC DEVICESExercise:More than One Option is Correct
Explore 3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBook:DC PANDEY ENGLISHChapter:SOLVD PAPERS 2017 NEET, AIIMS & JIPMERExercise:Solved paper 2018(JIPMER)
Explore 38 Videos
Similar Questions
Knowledge Check
The pressure inside a liquid of density ρ at a depth h is :
AhρgBhρgChρgDhρThe pressure at depth h below the surface of a liquid of density ρ open to the atmosphere is
Agreater than the atmospheric pressure by ρghBless than the atmospheric pressure by ρghCequal to the atmospheric pressureDincreases exponentially with depth
A small ball of density ρ is immersed in a liquid of density σ(>ρ) to a depth h and released. The height above the surface of water up to which the ball will jump is
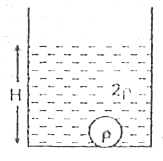
View SolutionA small ball of density ρ is placed from the bottom of a tank in which a non viscous liquid of density 2ρ is filled . Find the time taken by the ball to reach the surface of liquid and maximum height reached above the bottom of container . (Size of the ball and any type of drag force acting on the ball are negligible )
View SolutionA solid cube of side a and density ρ0 floats on the surface of a liquid of density ρ. If the cube is slightly pushed downward, then it oscillates simple harmonically with a period of
View SolutionA small ball is dropped from a certain height on the surface of a non-viscous liquid of density less than the density of ball. The motion of the ball is
View SolutionA small spherical ball of radius r is released from its completely submerged Position (as shown in the figure) in a liquid whose density varies with height h (measured from the bottom) as ρL=ρ0[4−(3h/h0)].The density of the ball is (5/2)ρ0. The height of the vessel is h0=12/π2 Consider r<<h0 and g=10m/s2.

Where will the ball come in the equilibrium?
View SolutionA small spherical ball of radius r is released from its completely submerged Position (as shown in the figure) in a liquid whose density varies with height h (measured from the bottom) as ρL=ρ0[4−(3h/h0)].The density of the ball is (5/2)ρ0. The height of the vessel is h0=12/π2 Consider r<<h0 and g=10m/s2.

The motion of the ball in the vessel is
View Solution

