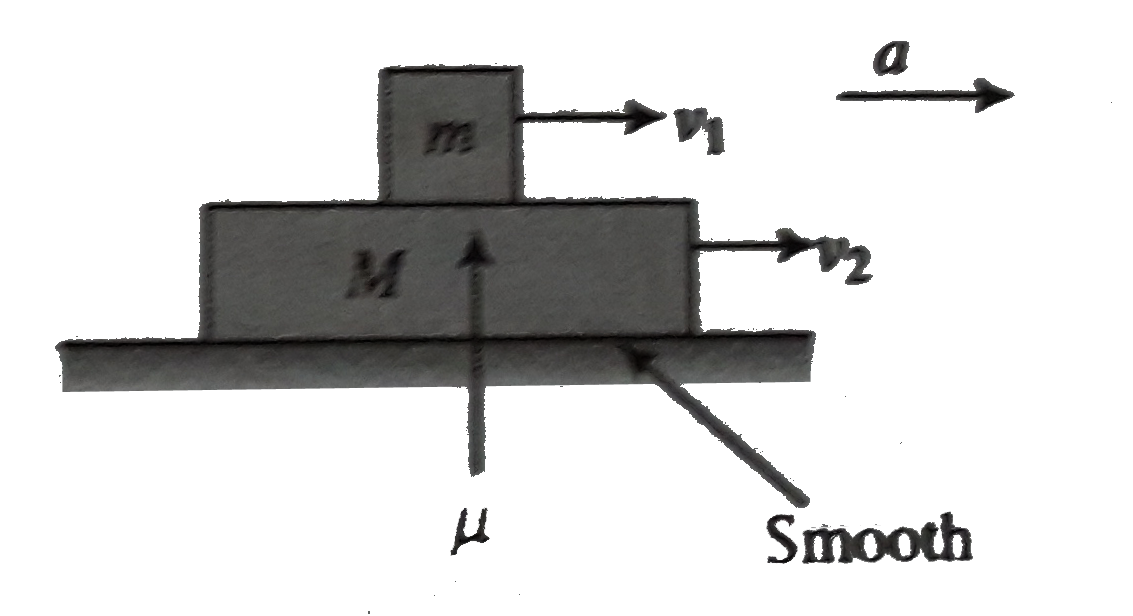
A small block of mass m is plced over a long plank of mass M the coefficient of friction between then is μ ground is smooth At t=0m is given a velocity v1 and M a velocity v2(>v1) as shown in figure After this M is maintained at constant celeration a(<μg)
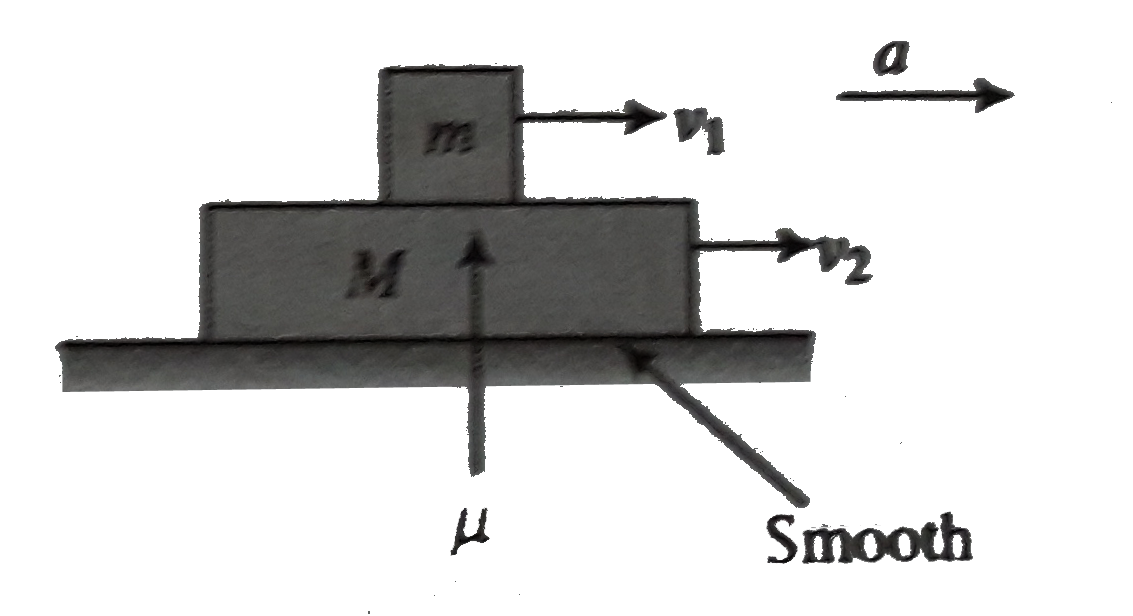
Initially there will be some relative motion between the block and the plank ,but after some time relative motion will cease and velocities of both will become
Draw the velocity of block as a function of time.
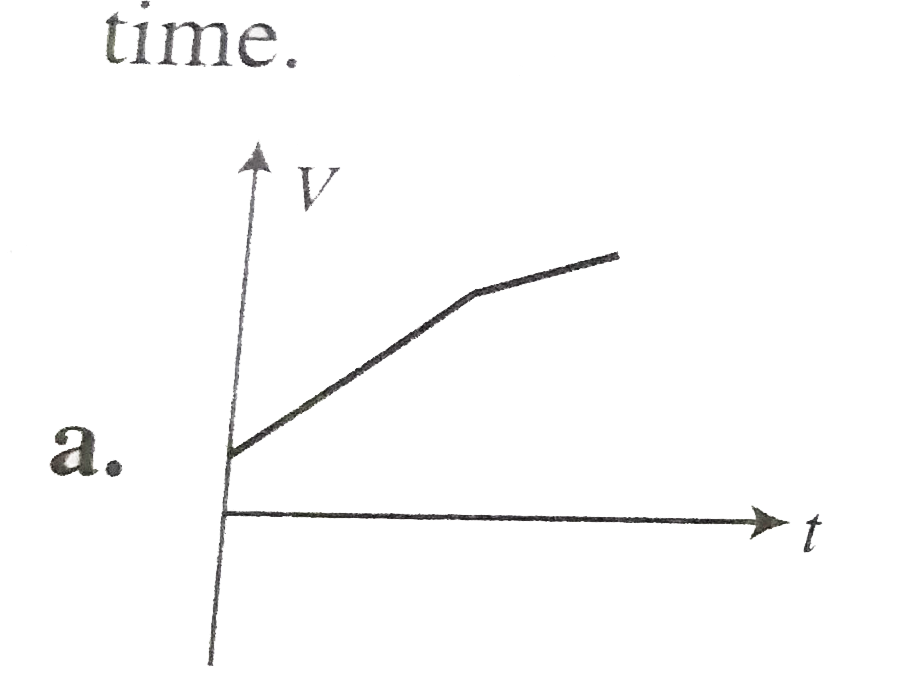
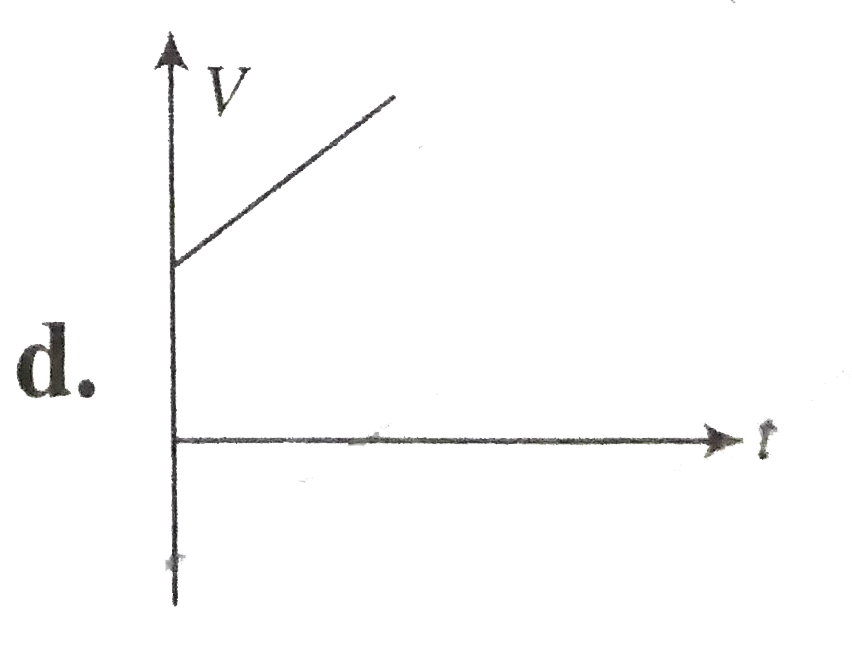
The correct Answer is:a
For t<t0
velocity of block at any time vb=v1+μ> stope of graph is μg velocity of block att=t0:=v1+μ>0
or t<t0
velocity of block at any time vb=v1+(mg−a)t0+at
Slope of graph will decrease hence correct graph is (a)
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer
6 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - True And False
4 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Multiple Correct
2 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
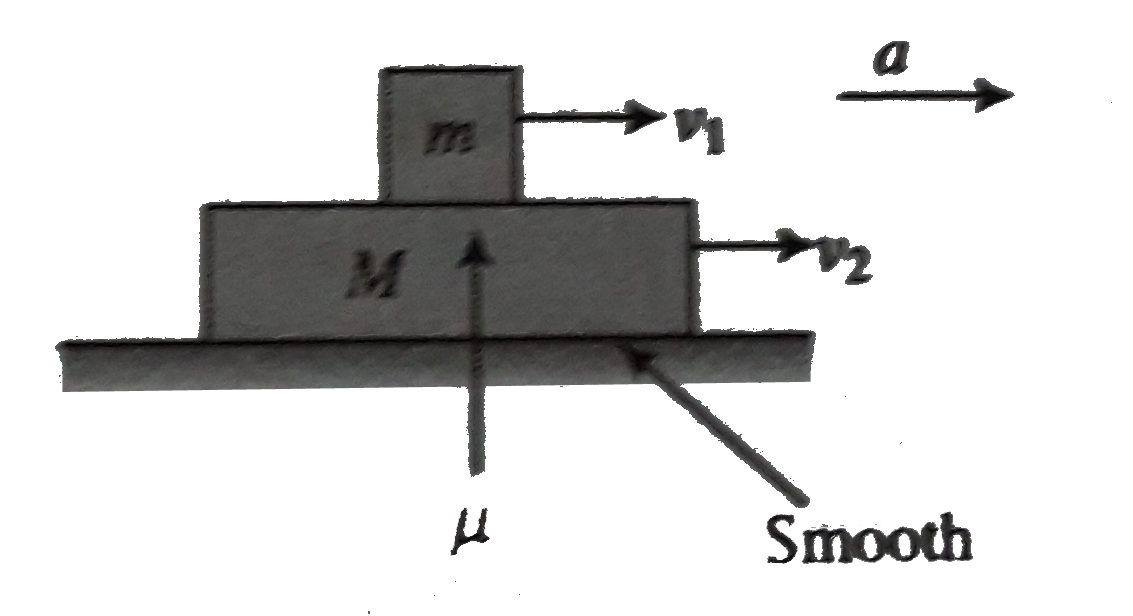
A small block of mass m is plced over a long plank of mass M the coefficient of friction between then is μ ground is smooth At t=0 m is given a velocity v1 and M a velocity v2(>v1) as shown in figure After this M is maintained at constant celeration a(<μg)
Initially there will be some relative motion between the block and the plank ,but after some time relative motion will cease and velocities of both will become
Find the forward force acting on the plank before after t0 respectively.
View SolutionA small block of mass m is plced over a long plank of mass M the coefficient of friction between then is μ .Ground is smooth At t=0 m is given a velocity v1 and M a velocity v2(>v1) as shown in Fig. After this M is maintained at constant celeration a(<μg)
Initially there will be some relative motion between the block and the plank ,but after some time relative motion will cease and velocities of both will become
Find the time t0 when the velocities of both block and plank become same.
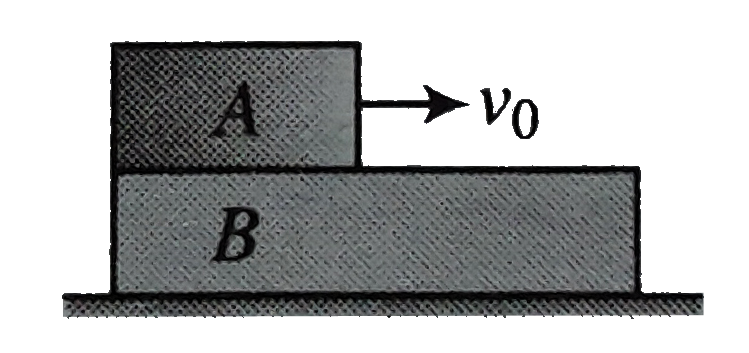
View SolutionA block A of mass m is placed over a plank B of mass 2m. Plank B is placed over a smooth horizontal surface. The coefficient of friction between A and B is 12 block A is given a velocity v0 towards right. Accelration of B relative to A is

View SolutionA block A of mass m is placed over a plankB of mass 2m plank B is placed over a smooth horizontal surface .The coefficient of friction between A and B is 0.4 Block A is given a velocity v0 toward right Find acceleration (in ms−2 of B relative to A
View SolutionA block of mass m is placed on the top of another block of mass M as shown in the figure. The coefficient of friction between them is μ.

The maximum acceleration with which the block M may move so that m also moves along with it is
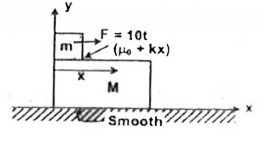
View SolutionA block of mass m is kept on an another block of mass M. The coefficient of friction between the blocks varies as μ=(μ0+kx) while friction between lower block and ground is zero. A time varying force F = 10t is applied horizontally on the upper block. Find time t0 when relative motion will start between the blocks. (x is relative displacement between the blocks.)
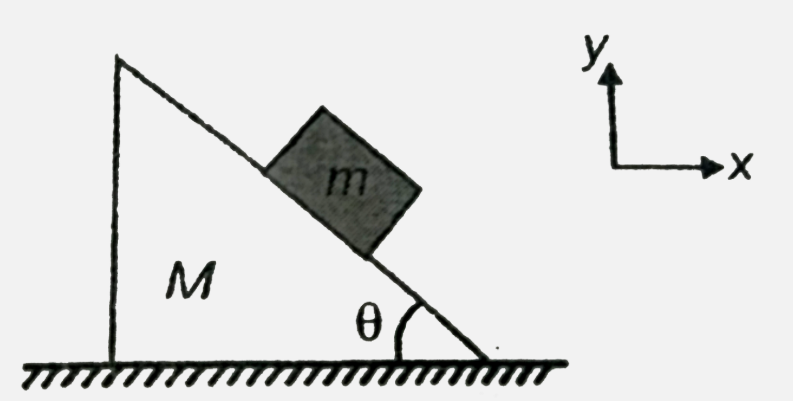
View SolutionA block of mass m is placed on a smooth wedge of mass M, as shown in the figure . Just after placiing block m over wedge M.
View SolutionIn fig Block m2 is loaded on block m1 . If there is no relative sliding between the block and the inclined plane is smooth , find the friction force between the block

View SolutionA small block of mass 1kg is placed over a plank of mass 2kg. The length of the plank is 2 m. coefficient of friction between the block and the plnak is 0.5 and the ground over which plank in placed is smooth. A constant force F=30N is applied on the plank in horizontal direction. the time after which the block will separte from the plank is (g=10m/s2)
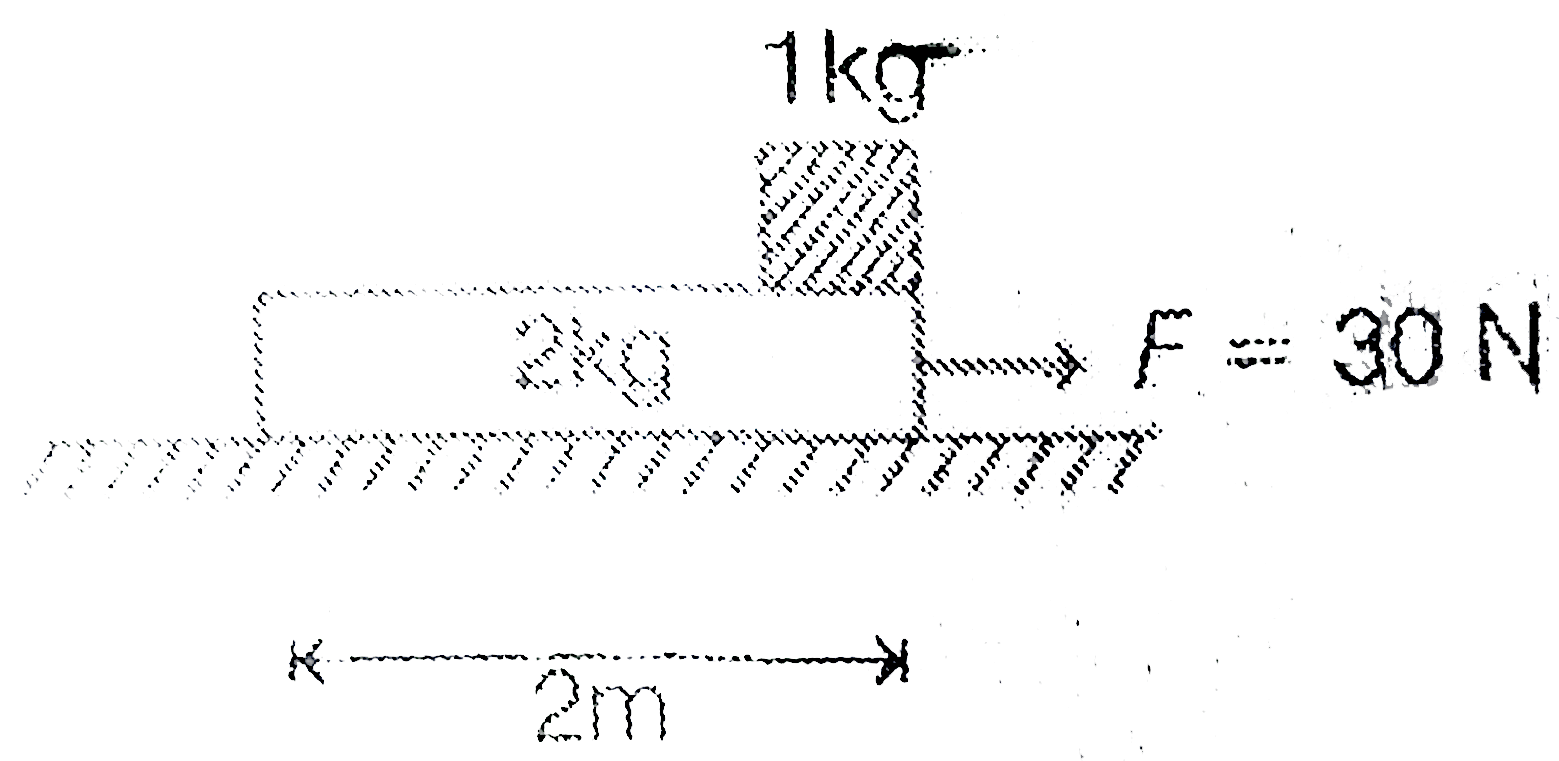
View SolutionA block of mass m is kept over another block of mass 2m. Coefficient of friction between two blocks is μ and that of between lower blood from the horizontal surface is zero. A horizontal force F=43μmg is applied on the block of mass 2m. Acceleration of lower block is
View Solution
