A small block of mass M moves with velocity 5 m/s towards an another block of same mass M placed at a distance of 2 m on a rough horizontal surface . Coefficient of friction between the blocks and ground is 0.25 . Collision between the two blocks is elastic , the separation between the blocks , when both of them come to rest , is ( g = 10m/s2)
3 m
4 m
2 m
1.5 m
To solve the problem, we will follow these steps:
Step 1: Determine the acceleration due to friction
The acceleration due to friction can be calculated using the formula:
a=μ⋅g
where:
- μ=0.25 (coefficient of friction)
- g=10m/s2 (acceleration due to gravity)
Substituting the values:
a=0.25⋅10=2.5m/s2
Since friction acts opposite to the direction of motion, we will consider this acceleration as negative:
a=−2.5m/s2
Step 2: Calculate the distance traveled by the first block before it comes to rest
Using the kinematic equation:
v2f=v2i+2as
where:
- vf=0m/s (final velocity when the block comes to rest)
- vi=5m/s (initial velocity of the first block)
- a=−2.5m/s2 (acceleration due to friction)
- s is the distance traveled before coming to rest.
Substituting the values:
0=(5)2+2(−2.5)s
0=25−5s
5s=25
s=255=5m
Step 3: Determine the time taken for the first block to come to rest
Using the equation:
vf=vi+at
Substituting the known values:
0=5−2.5t
2.5t=5
t=52.5=2s
Step 4: Calculate the initial velocity of the second block after the collision
Since the collision is elastic, the first block transfers some of its momentum to the second block. The initial velocity of the second block after the collision can be calculated using the conservation of momentum and the fact that the two blocks have the same mass M.
Let v1 be the final velocity of the first block after the collision and v2 be the final velocity of the second block:
Using the conservation of momentum:
M⋅5+M⋅0=M⋅v1+M⋅v2
Since the collision is elastic, we also have:
v1+v2=5
From the above two equations, we can solve for v1 and v2. However, since we know the first block comes to rest, we can assume:
v1=0
Thus,
v2=5m/s
Step 5: Calculate the distance traveled by the second block before it comes to rest
Using the same friction force, the second block will also experience the same deceleration:
a=−2.5m/s2
Using the kinematic equation again:
0=(5)2+2(−2.5)s
0=25−5s
5s=25
s=5m
Step 6: Calculate the total separation between the two blocks
The total separation between the two blocks when they come to rest is the distance traveled by the first block before coming to rest plus the distance traveled by the second block:
Total Separation=Distance traveled by first block+Distance traveled by second block
Total Separation=5+5=10m
Final Answer
The separation between the blocks when both of them come to rest is 10 m.
---
The acceleration due to friction can be calculated using the formula:
a=μ⋅g
where:
- μ=0.25 (coefficient of friction)
- g=10m/s2 (acceleration due to gravity)
a=0.25⋅10=2.5m/s2
a=−2.5m/s2
Using the kinematic equation:
v2f=v2i+2as
where:
- vf=0m/s (final velocity when the block comes to rest)
- vi=5m/s (initial velocity of the first block)
- a=−2.5m/s2 (acceleration due to friction)
- s is the distance traveled before coming to rest.
0=(5)2+2(−2.5)s
0=25−5s
5s=25
s=255=5m
Using the equation:
vf=vi+at
Substituting the known values:
0=5−2.5t
2.5t=5
t=52.5=2s
Since the collision is elastic, the first block transfers some of its momentum to the second block. The initial velocity of the second block after the collision can be calculated using the conservation of momentum and the fact that the two blocks have the same mass M.
Using the conservation of momentum:
M⋅5+M⋅0=M⋅v1+M⋅v2
Since the collision is elastic, we also have:
v1+v2=5
v1=0
Thus,
v2=5m/s
Using the same friction force, the second block will also experience the same deceleration:
a=−2.5m/s2
0=(5)2+2(−2.5)s
0=25−5s
5s=25
s=5m
The total separation between the two blocks when they come to rest is the distance traveled by the first block before coming to rest plus the distance traveled by the second block:
Total Separation=Distance traveled by first block+Distance traveled by second block
Total Separation=5+5=10m
The separation between the blocks when both of them come to rest is 10 m.
Topper's Solved these Questions
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - More a than one option is Correct
1 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
Similar Questions
The friction coefficient between the horizontal surfce and ech of the blocks shown in figure is 0.20. The collision between the blocks is perfectly elastic. Find the separation between the two blocks when they come to rest. Take g=10ms2.
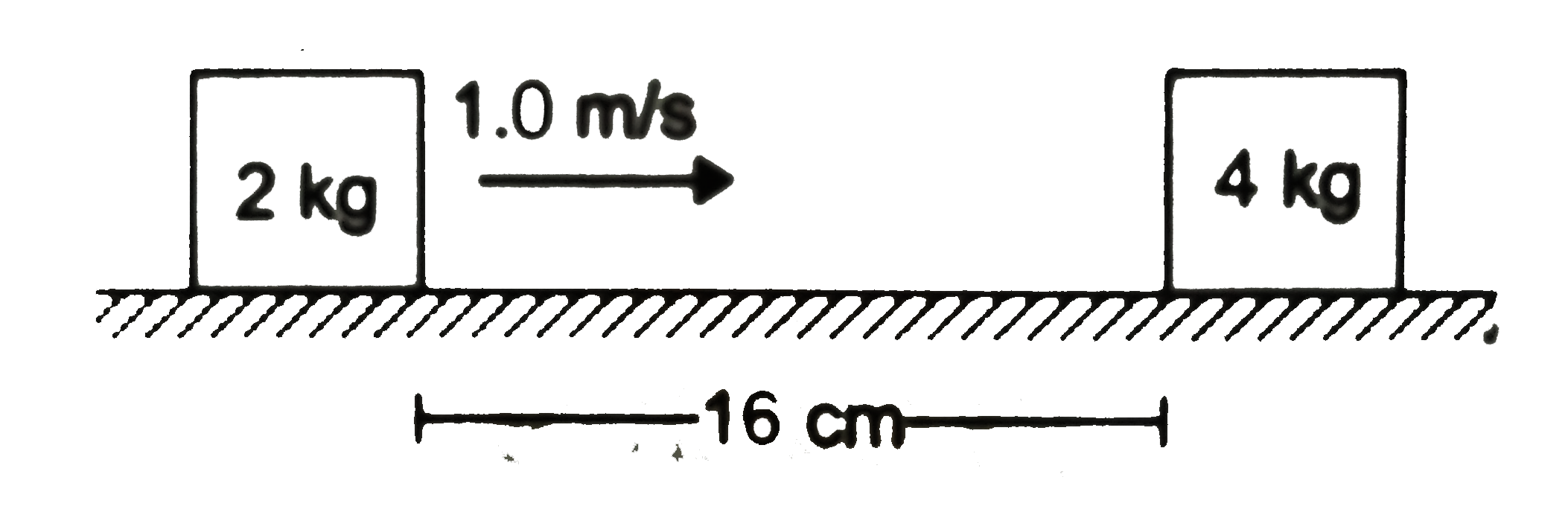
View SolutionThe friction coefficient between the horizontal surface and each of the block shown in the figure is 0.2. The collision between the blocks is perfectly elastic. Find the separation between them when they come to rest. (Take g=10m/s2).

View Solution
Knowledge Check
A block of mass 1 kg lies on a horizontal surface in a truck. The coefficient of static friction between the block and the surface is 0.6. If the acceleration of the truck is 5m/s2, the frictional force acting on the block is…………newtons.
A10NB5NC2.5ND20N
A block of mass m is moving on a rough horizontal surface. μ is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
View SolutionA block of mass m is pulled by a force of constant power P placed on a rough horizontal plane. The friction coefficient between the block and the surface is μ. Then
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal. If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View SolutionA block is kept on a rough horizontal surface as shown. Its mass is 2 kg and coefficient of friction between block and surface (μ)=0.5. A horizontal force F is acting on the block. When

View SolutionA block of mass m is pulled by a constant powert P placed on a rough horizontal plane. The friction coefficient the block and surface is μ. The maximum velocity of the block is.
View SolutionA block of mass 1 kg lies on a horizontal surface in a truck. The coefficient of static friction between the block and the surface is 0.6. If the acceleration of the truck is 5m/s2, the frictional force acting on the block is…………newtons.
View SolutionA block of mass m is kept over another block of mass 2 m and the system rests on a smooth horizontal surface. The coefficient of friction between the blocks is 0.50. Find the work done by the force of friction on the smaller block by the bigger block during a displacement d of the system, when a force mg is applied to the lower block.
View Solution
