A small block of mass m resting at the bottom of a hemispherical cup of radius R is displaced a little and released. Determine the period of oscillations of the block, assuming the cup to be smooth and fixed rigidly to the table on which it rests. How will period change if the cup is free to move on the table, it is smooth and its mass is M?
The correct Answer is:T=2π√R/g,T=2π ⎷Rg(1+mM)
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - NN GHOSHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Eexercies
39 Videos
- SIMPLE AND COMPOUND PENDULUMBOOK - NN GHOSHCHAPTER - SIMPLE AND COMPOUND PENDULUMEXERCISE - Exercise
24 Videos
- SPECIFIC HEAT CAPACITY OF GASESBOOK - NN GHOSHCHAPTER - SPECIFIC HEAT CAPACITY OF GASESEXERCISE - All Questions
17 Videos
Similar Questions
A small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure Choose the wrong option.

View SolutionA small body of mass m slide without friction from the top of a hemispherical cup of radius r as shown in figure. If leaves the surface to the cup at vertial distance h below the highest point then
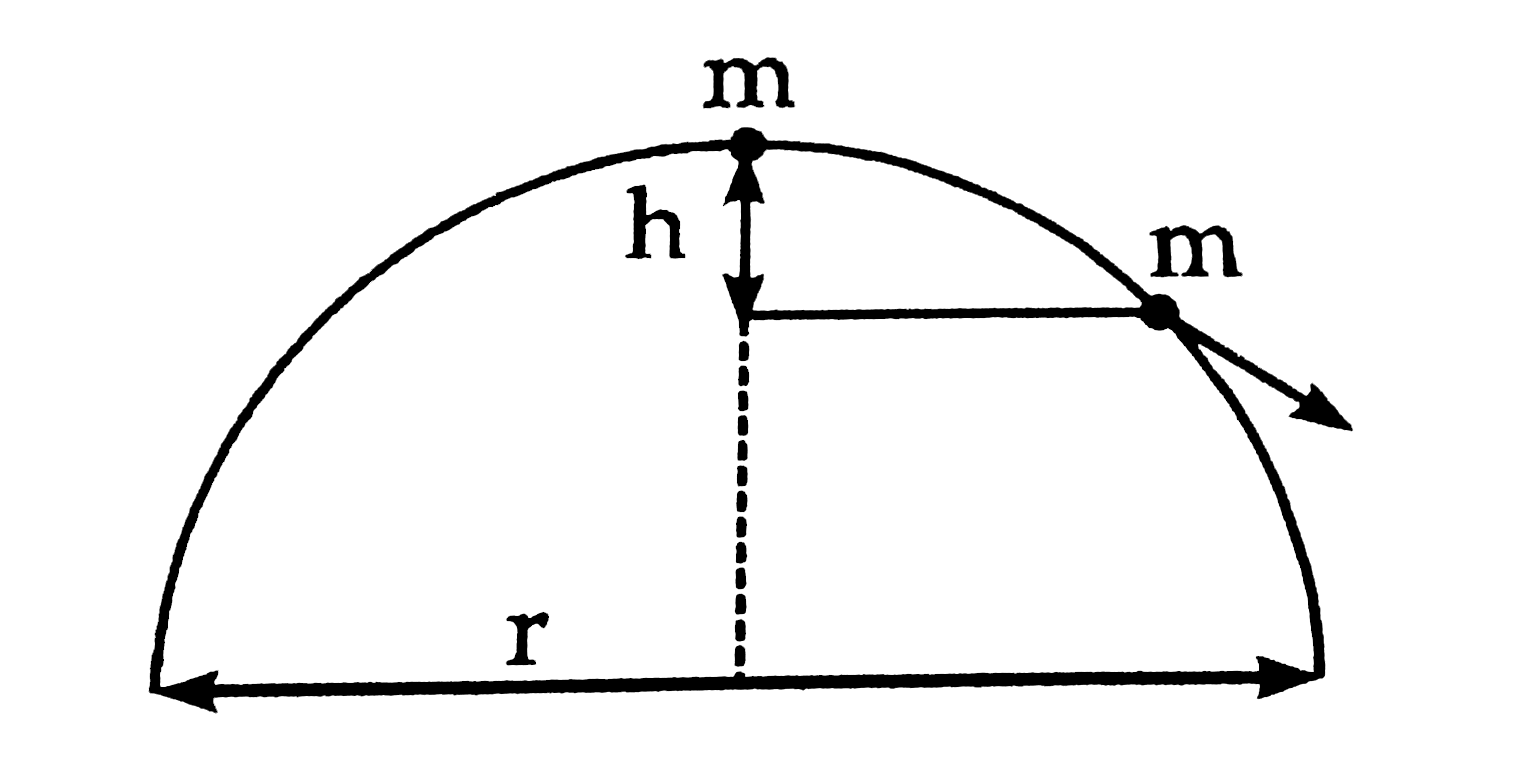
View Solution
Knowledge Check
A block of mass m rigidly attached with a spring k is compressed through a distance A. If the block is released, the period of oscillation of the block for a complete cycle is equal to
 A4π3√mkBπ√2√mkC2π3√mkDNone of these
A4π3√mkBπ√2√mkC2π3√mkDNone of theseA small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure Choose the wrong option.
 AAcceleration of block is constant throughoutBAcceleration of block is g at ACAcceleration of block is 3g at BDAcceleration of block is 2g at B
AAcceleration of block is constant throughoutBAcceleration of block is g at ACAcceleration of block is 3g at BDAcceleration of block is 2g at BA small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure. Choose the wrong option (s)
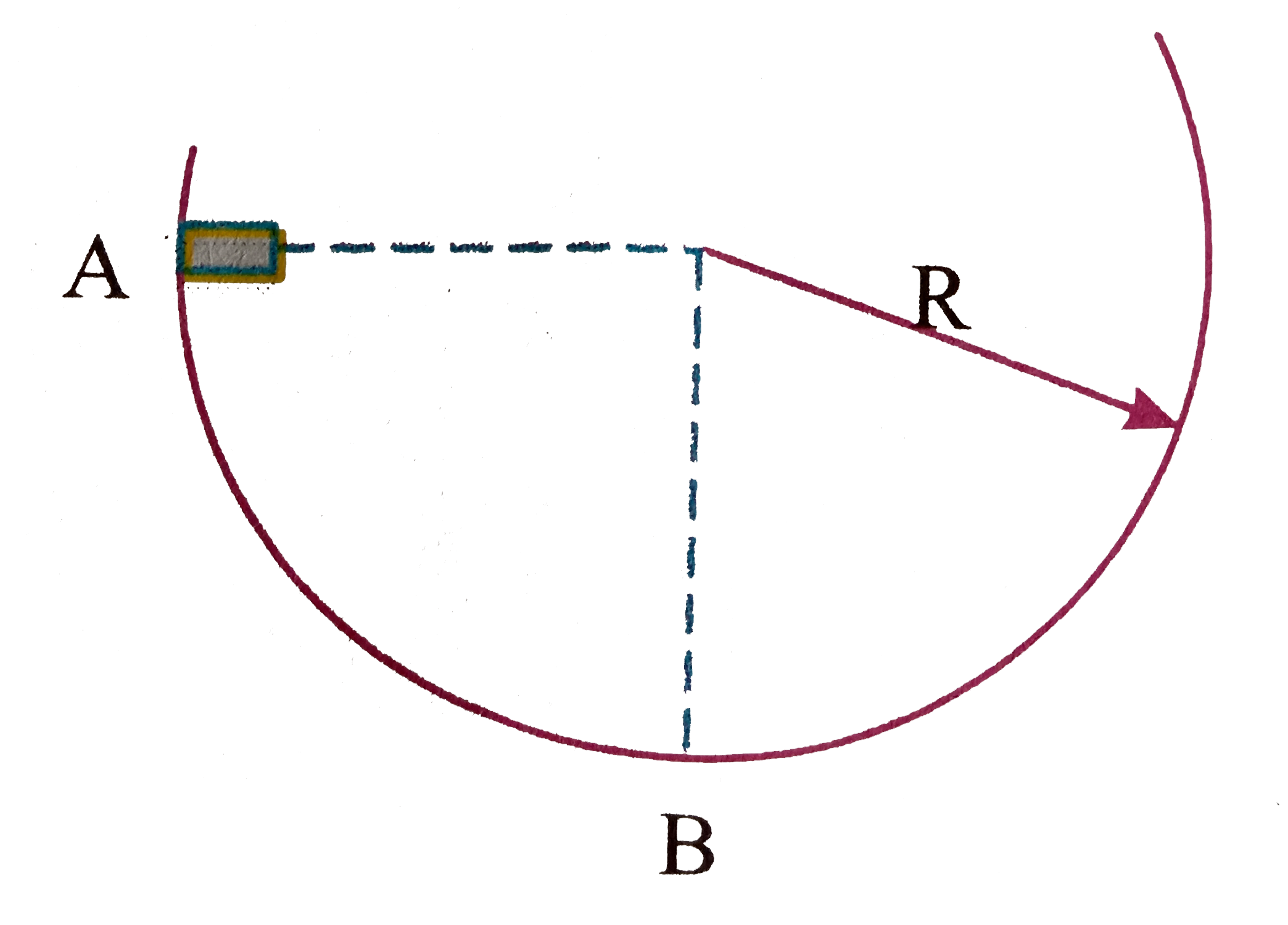 Aacceleration to block is constant throughoutBacceleration of block is g at ACacceleration of block is 3g at BDacceleration of block is 2g at B
Aacceleration to block is constant throughoutBacceleration of block is g at ACacceleration of block is 3g at BDacceleration of block is 2g at B
If in the above problem the block is replaced by a small spherical ball of radius r and the cup is fixed, what will be the period of oscillations of the ball?
View SolutionA block of mass m is connected to three springs as shown in Fig. The block is displaced down slightly and left free, it starts oscillating. Find time period of oscillations.
View SolutionA block of mass m connected with a smooth prismatic wedge of mass M is released from rest when the spring is relaxed. Find the angular frequency of oscillation.

View SolutionA block of mass m connected with a smooth prismatic wedge of mass m is released from rest when the spring is relaxed. Find the angular frequency of oscillation.

View SolutionFind the gravitational potential due to a hemispherical cup of mass M and radius R, at its centre of curvature.
View Solution
