A small body of mass m is fixed to the middle of a stretched string of length 2l. In the equlibrium position the string tension is equal to T0. Find the angular freqency of small oscillations of the body in the transverse direction. The mass of the string is negligible, the gravitational field is absent.
To find the angular frequency of small oscillations of a mass m fixed to the middle of a stretched string of length 2l with tension T0, we can follow these steps:
Step 1: Understand the system
The mass m is suspended at the midpoint of a string of length 2l. Since the gravitational field is absent, the only forces acting on the mass are due to the tension in the string.
Step 2: Draw the free body diagram
When the mass is displaced slightly from its equilibrium position, the string will form an angle θ with the vertical. The tension T0 acts along the string, and we can resolve this tension into two components:
- A vertical component T0cosθ
- A horizontal component T0sinθ
Step 3: Determine the restoring force
The restoring force acting on the mass when it is displaced by a small distance x can be derived from the horizontal component of the tension. Since the mass is displaced downwards, the restoring force F is given by:
F=2T0sinθ
For small angles, we can use the approximation sinθ≈xl. Thus, we can write:
F≈2T0xl
Step 4: Relate the restoring force to acceleration
According to Newton's second law, the restoring force is also equal to the mass times the acceleration:
F=ma
where a is the acceleration of the mass. In simple harmonic motion, acceleration can be expressed as:
a=−ω2x
where ω is the angular frequency. Therefore, we have:
2T0xl=m(−ω2x)
Step 5: Simplify the equation
We can cancel x from both sides (assuming x≠0):
2T01l=−mω2
Rearranging gives:
ω2=2T0ml
Step 6: Solve for angular frequency
Taking the square root of both sides, we find:
ω=√2T0ml
Final Answer
The angular frequency of small oscillations of the body in the transverse direction is:
ω=√2T0ml
---
The mass m is suspended at the midpoint of a string of length 2l. Since the gravitational field is absent, the only forces acting on the mass are due to the tension in the string.
When the mass is displaced slightly from its equilibrium position, the string will form an angle θ with the vertical. The tension T0 acts along the string, and we can resolve this tension into two components:
- A vertical component T0cosθ
- A horizontal component T0sinθ
The restoring force acting on the mass when it is displaced by a small distance x can be derived from the horizontal component of the tension. Since the mass is displaced downwards, the restoring force F is given by:
F=2T0sinθ
For small angles, we can use the approximation sinθ≈xl. Thus, we can write:
F≈2T0xl
According to Newton's second law, the restoring force is also equal to the mass times the acceleration:
F=ma
where a is the acceleration of the mass. In simple harmonic motion, acceleration can be expressed as:
a=−ω2x
where ω is the angular frequency. Therefore, we have:
2T0xl=m(−ω2x)
We can cancel x from both sides (assuming x≠0):
2T01l=−mω2
Rearranging gives:
ω2=2T0ml
Taking the square root of both sides, we find:
ω=√2T0ml
The angular frequency of small oscillations of the body in the transverse direction is:
ω=√2T0ml
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electric Oscillations
56 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Elastic Waves
39 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
A bird with mass m parches at the middle of a strectched string Show that the tension in the string is give by T=mg2sinθ. Assuming that each half of the string is straight.

View SolutionA small body of mass m is tried to a string and revolved in a vertical circle of radius r. If the tension in the string at the highest point is mg, what is its speed there?
View Solution
Knowledge Check
A body of mass 60 kg suspended by means of three strings, P, Q and R as shown in the figure is in equlibrium. The tension in the string P is
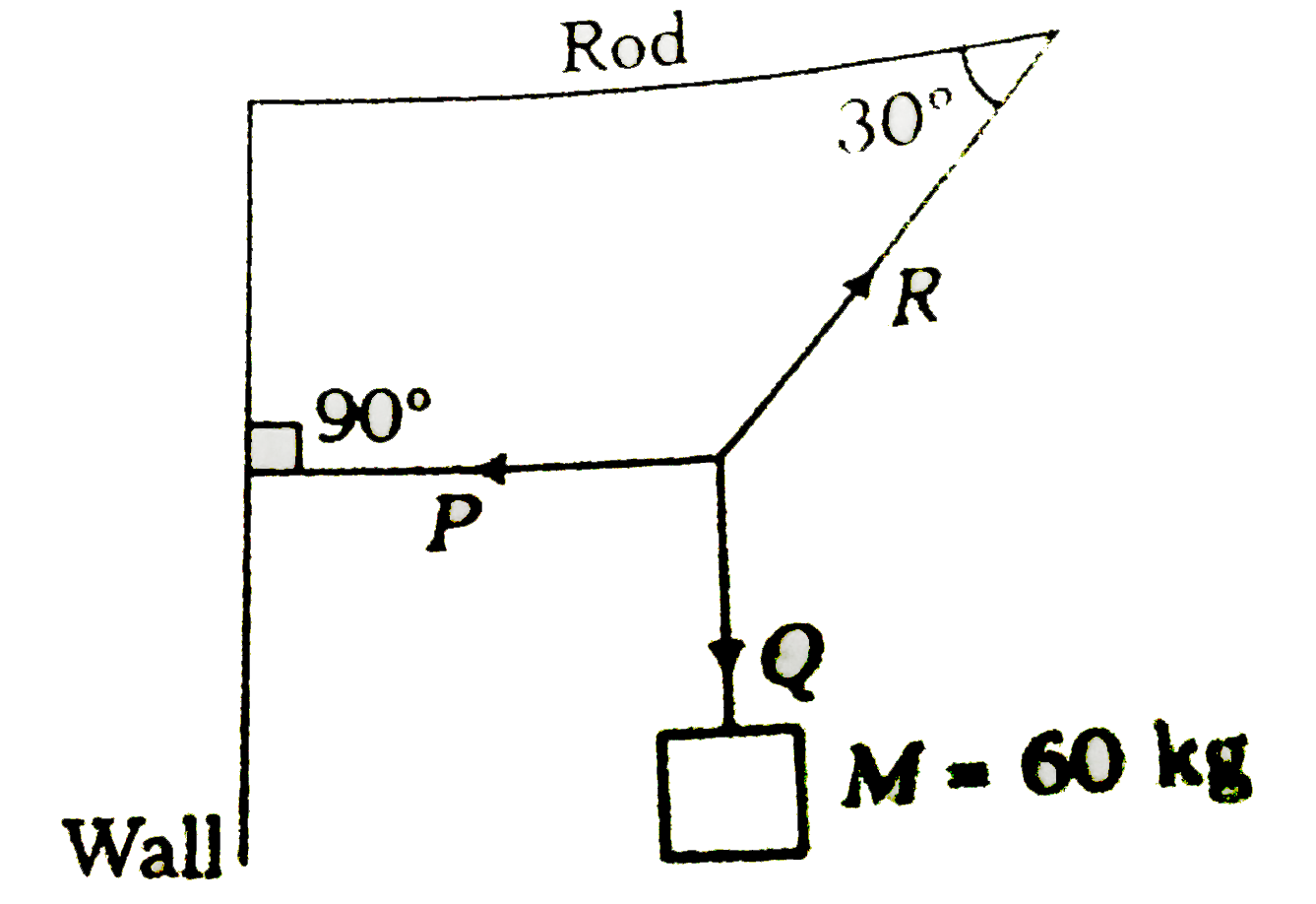 A130.9 kgfB60 kgfC50 kgfD103.9 kgf
A130.9 kgfB60 kgfC50 kgfD103.9 kgfTwo balls of mass m and 2m are attached with strings of length 2L and L respectively. They are released from horizontal position. Find ratio of tensions in the string when the acceleration of both is only in vertical direction :
A3:5B4:5C2:5D1:2A bead of mass m is attached to the mid-point of a taut, weightless string of length l and placed on a frictionless horizontal table.
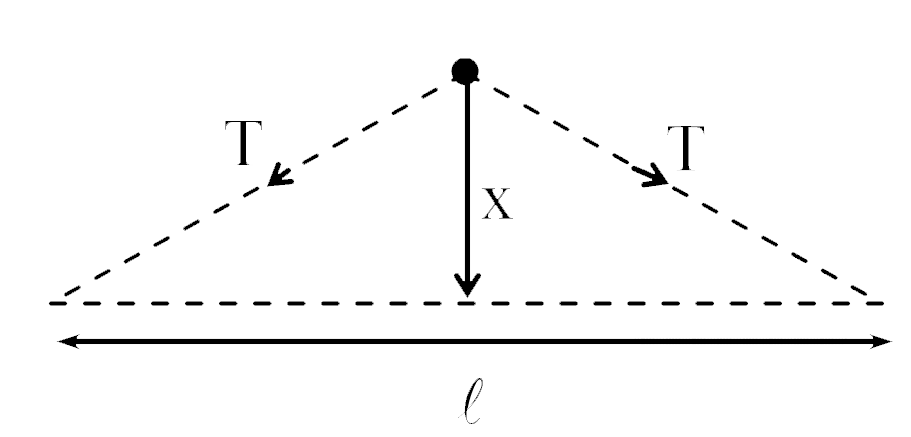
Under a small transverse displacement x, as shown, if the tension in the string is T, then the frequency of oscillation is-A12π√2TmlB12π√4TmlC12π√4TmD12π√2Tm
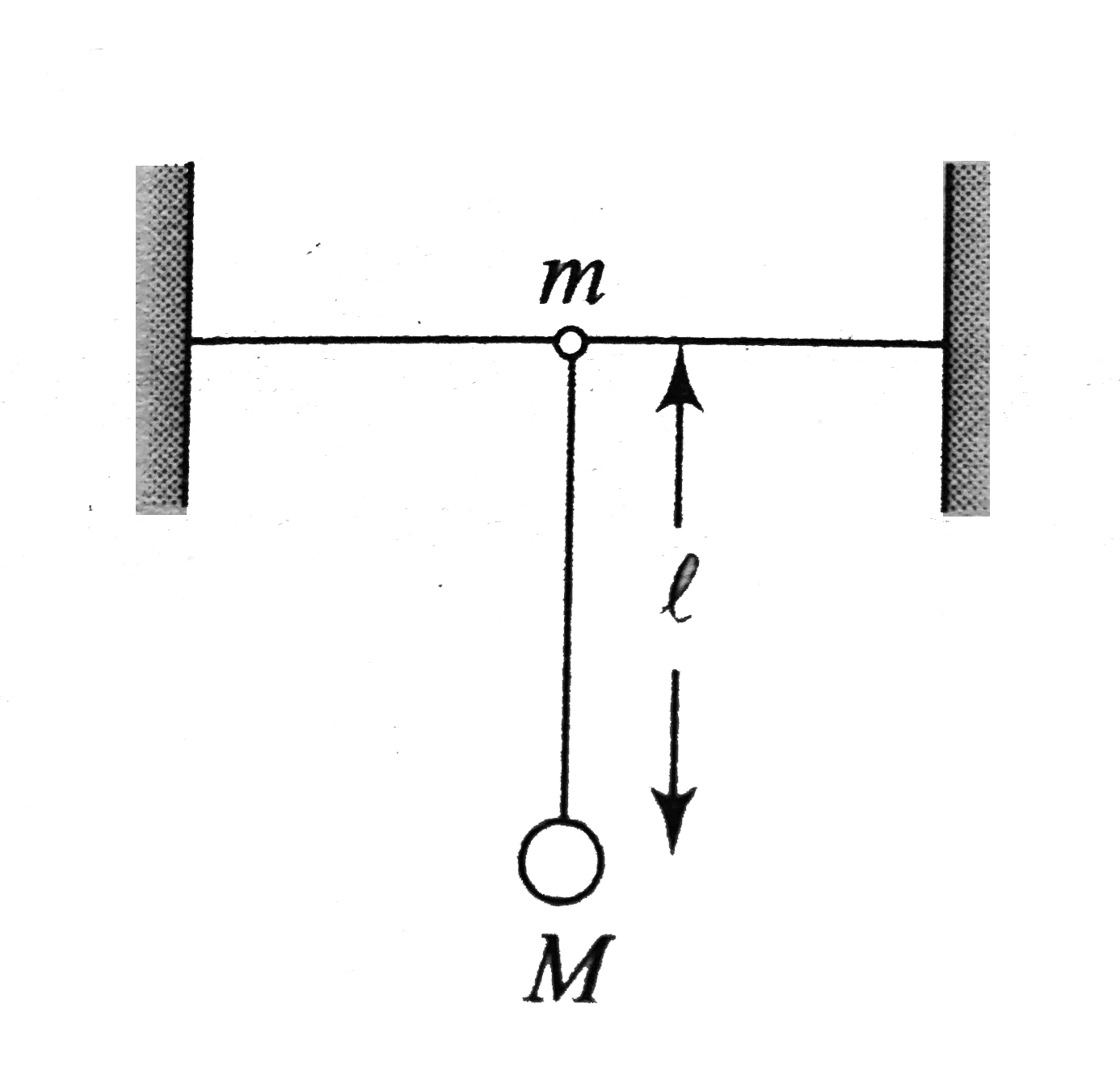
A smooth of mass m1 is lying on a rigid horizontal string A bob of mass m2 hangs from, the ring by an inextensible light string of length l. Find angular frequency of oscillation of the system.
View SolutionA body of mass mis suspended by two strings making angles αandβ with the horizontal. Find the tensions in the strings.
View SolutionA body of mass M is hanging by an inextensible string of mass m. If the free end of the string accelerates up with constant acceleration a. find the variation of tension in the string a fuction of the distance measured from the mass M (bottom of the string).

View SolutionA block of mass m hangs by means of a string which goes over a pulley of mass m and moment of inertia l, as shown in the diagram. The string does not relative to the pulley. Find the frequency of small oscillations.
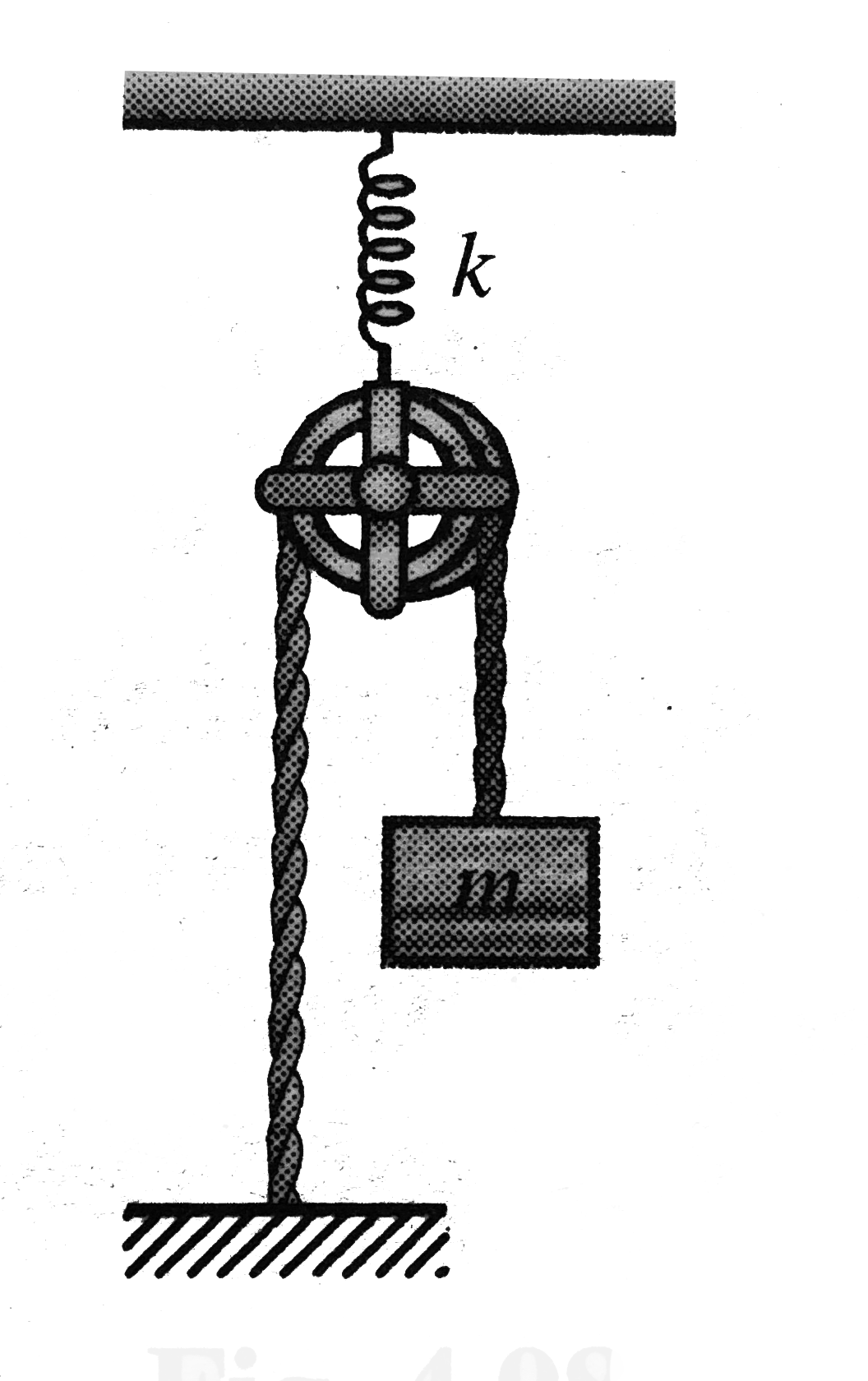
View SolutionA body of mass m is tied to a string of length l and whirled in a verticle cirlce. The velocity of the body at the lowest position is u. Then the tension in the string at a position when the string makes an angle θ with the vertical is
View Solution
