A small creature moves with constant speed in a vertical circle on a bright day. Does its shadow formed by the sun on horizontal plane move in a simple harmonic motion?
To determine whether the shadow of a small creature moving in a vertical circle exhibits simple harmonic motion (SHM), we can analyze the situation step by step.
Step 1: Understand the Motion of the Creature
The creature is moving with constant speed in a vertical circle. This means that it is undergoing circular motion, where its position changes continuously as it moves along the circular path.
Hint: Visualize the circular path and the position of the creature at different points in time.
Step 2: Analyze the Shadow Formation
As the creature moves in a vertical circle, the position of the creature changes, which in turn affects the position of its shadow on the horizontal plane. The shadow is formed due to the sunlight, which can be considered as coming from a fixed point (the sun).
Hint: Consider how the angle of the sun affects the position of the shadow on the horizontal plane.
Step 3: Determine the Path of the Shadow
When the creature moves in a vertical circle, the shadow will trace a path on the horizontal plane. The vertical circular motion of the creature translates into a horizontal motion of the shadow. Specifically, as the creature moves up and down in the vertical circle, the shadow will oscillate back and forth.
Hint: Think about how the vertical position of the creature corresponds to the horizontal position of the shadow.
Step 4: Identify the Characteristics of Simple Harmonic Motion
Simple harmonic motion is characterized by a restoring force that is proportional to the displacement from an equilibrium position. In this case, as the shadow moves, it will oscillate around a central point (the equilibrium position) and will have a maximum displacement (amplitude).
Hint: Recall the definition of SHM and check if the motion of the shadow meets these criteria.
Step 5: Conclusion
Since the shadow oscillates back and forth around a central position as the creature moves in a vertical circle, we can conclude that the shadow does indeed move in simple harmonic motion.
Final Answer: Yes, the shadow formed by the creature moving in a vertical circle does move in simple harmonic motion.
The creature is moving with constant speed in a vertical circle. This means that it is undergoing circular motion, where its position changes continuously as it moves along the circular path.
As the creature moves in a vertical circle, the position of the creature changes, which in turn affects the position of its shadow on the horizontal plane. The shadow is formed due to the sunlight, which can be considered as coming from a fixed point (the sun).
When the creature moves in a vertical circle, the shadow will trace a path on the horizontal plane. The vertical circular motion of the creature translates into a horizontal motion of the shadow. Specifically, as the creature moves up and down in the vertical circle, the shadow will oscillate back and forth.
Simple harmonic motion is characterized by a restoring force that is proportional to the displacement from an equilibrium position. In this case, as the shadow moves, it will oscillate around a central point (the equilibrium position) and will have a maximum displacement (amplitude).
Since the shadow oscillates back and forth around a central position as the creature moves in a vertical circle, we can conclude that the shadow does indeed move in simple harmonic motion.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective-2
7 Videos
Similar Questions
A particle moves with constant angular velocity in a circle. During the motion its
View SolutionA particle of mass m is moving with constant speed in a vertical circle in X−Z plane. There is a small both at some distance on Z−axis. The maximum distance of the shadow of the particle on X−axis from origin equal to :−
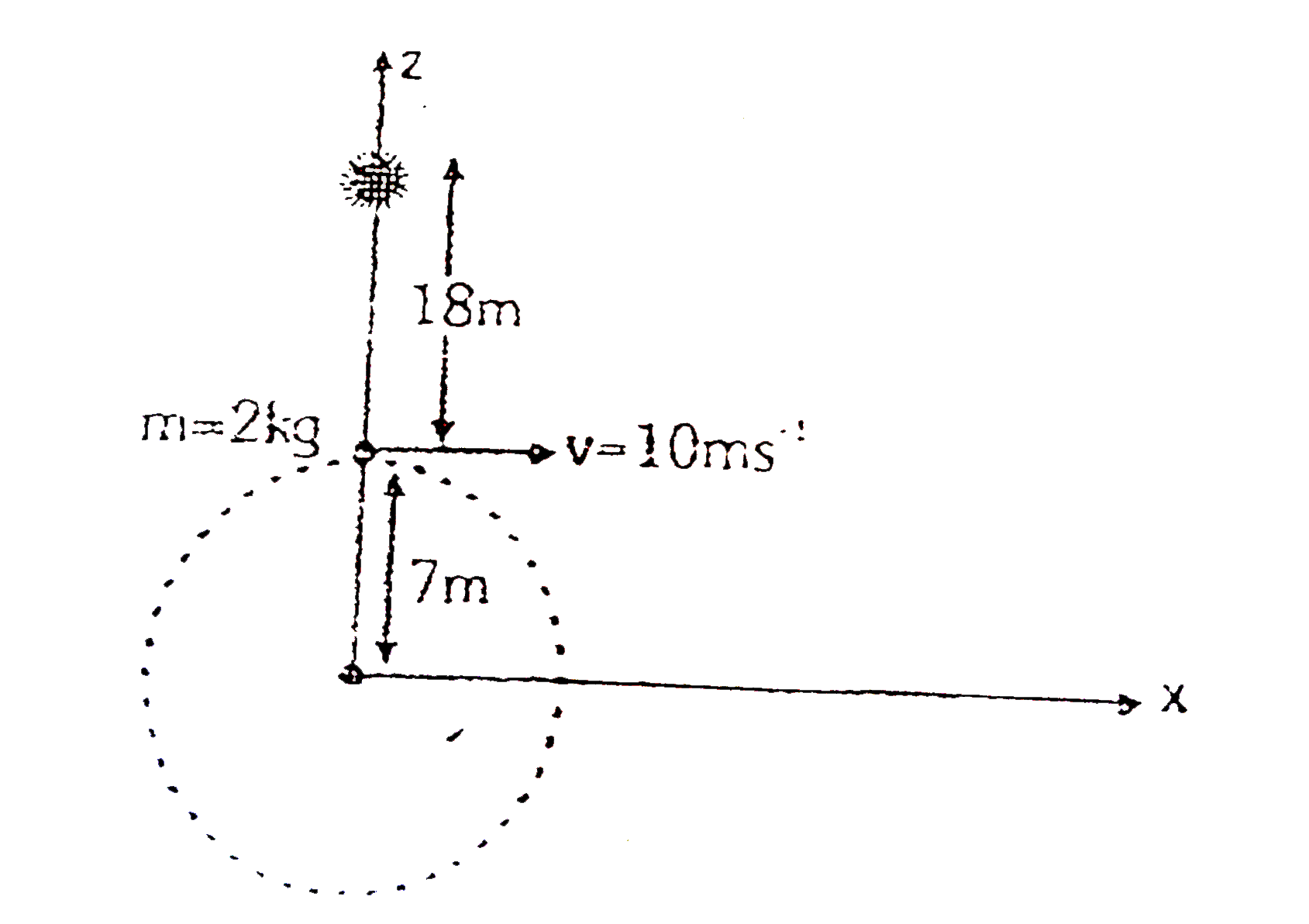
View SolutionA cart moves with a constant speed along a horizontal circular path. From the cart, a particle is thrown up vertically with respect to the cart.
View SolutionA car is moving along a circle with constant speed on an inclined plane as shown in diagram. Then friction force on car will be in horizontal direction at least at one point :

View SolutionA disc is hinged such that it can freely rotate in a vertical plane about a point on its radius. If radius of disc is 'R' , then what will be minimum time period of its simple harmonic motion ?
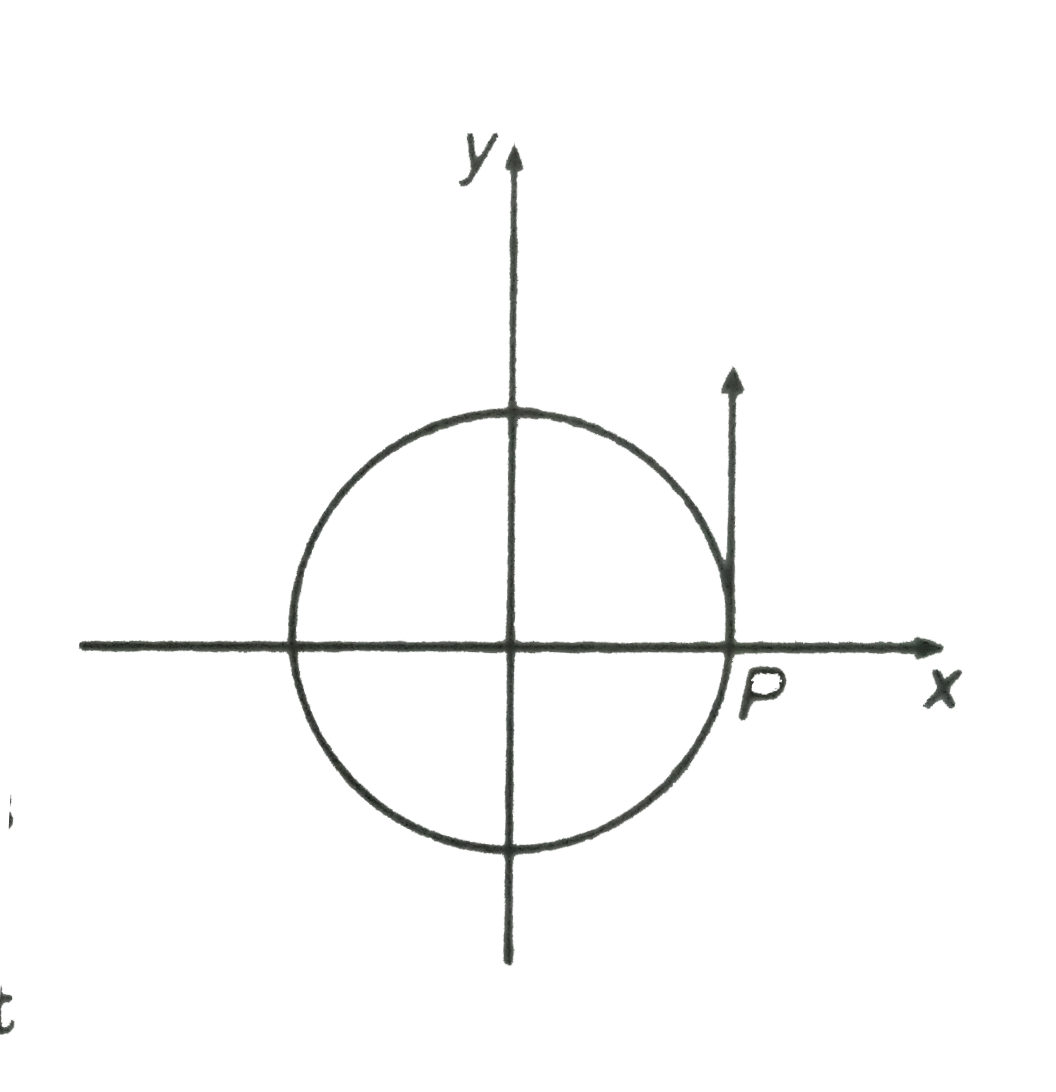
View SolutionA train is moving with a constant speed of 10m/s in a circle of radius 16πm. The plane of the circle lies in horizontal x-y plane. At time t = 0, train is at point P and moving in counter- clockwise direction. At this instant, a stone is thrown from the train with speed 10m/s relative to train towards negative x-axis at an angle of 37∘ with vertical z-axis . Find
(a) the velocity of particle relative to train at the highest point of its
trajectory.
(b) the co-ordinates of points on the ground where it finally falls and that of the hightest point of its trajectory. (Take g =10m/s2,sin37∘=35
View SolutionA particle moves with constant speed v along a regular hexagon ABCDEF in the same order. Then the magnitude of the avergae velocity for its motion form A to
View SolutionA particle of mass m moves with constant speed v on a circular path of radius r as shown in figure. The average force on it during its motion from A to B is

View SolutionA particle is moving with constant speed v in xy plane as shown in figure. The magnitude of its angular velocity about point O is

View SolutionA uniform disc is rotating at a constantt speed in a vertical plane about a fixed horizontal axis passing through the centre of the disc. A piece of the disc from its rim detaches itself from the disc at the instant when it is at horizontal level with the centre of the disc and moving upward. Then about the fixed axis, the angular speed of the
View Solution
