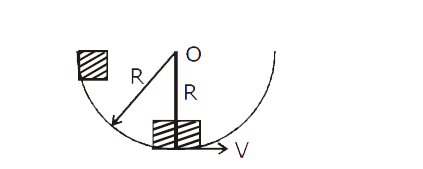
A small cube of mass m slides down a circular path of radius R cut into a large block of mass M, as shown in figure. M rests on a table, and both blocks move without friction. The blocks are initially at rest, and m starts from the top of the path. Find the horizontal distance from the bottom of block where cube hits the cable

The correct Answer is:B

mv1=Mv2 …(i)
mgR=12mv21+12Mv22 …(ii)
t=√2(R/2)g=√Rg …(iii)
The desired distance is
S=(v1+v2)t …(iv)
Solving Eqs. (i) and (ii) of v1 and v2 and substituting in Eq. (iv), we get
S=R√2M+mM
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Comprehension Based Questions
3 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
Knowledge Check
A block of mass 3 kg slides down an inclined plane of length 6 m and height 4 m. if the force of friction on the block is a constant 16 N as it slides from rest at the top of the incline, what is its speed at the bottom?
A2m/sB3m/sC4m/sD5m/s
A uniform solid cylinder of mass 2kg and radius 0.2m is released from rest at the top of a semicircular track of radius 0.7m cut in a block of mass M=3kg as shown in Fig. The block is resting on a smooth horizontal surface and the cylinder rolls down without slipping. Based on the above information, answer the following questions:

The distance moved by the block when the cylinder reaches the bottom of the track is
View SolutionA small block of mass m slides along a smooth frictional track as shown in the figure. If it starts from rest at P, what is the resultant force acting on it at Q?

View SolutionThe block of mass m is at rest. Find the tension in the string A .
View SolutionA small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure Choose the wrong option.

View SolutionA uniform solid cylinder of mass 2kg and radius 0.2m is released from rest at the top of a semicircular track of radius 0.7m cut in a block of mass M=3kg as shown in Fig. The block is resting on a smooth horizontal surface and the cylinder rolls down without slipping. Based on the above information, answer the following questions:
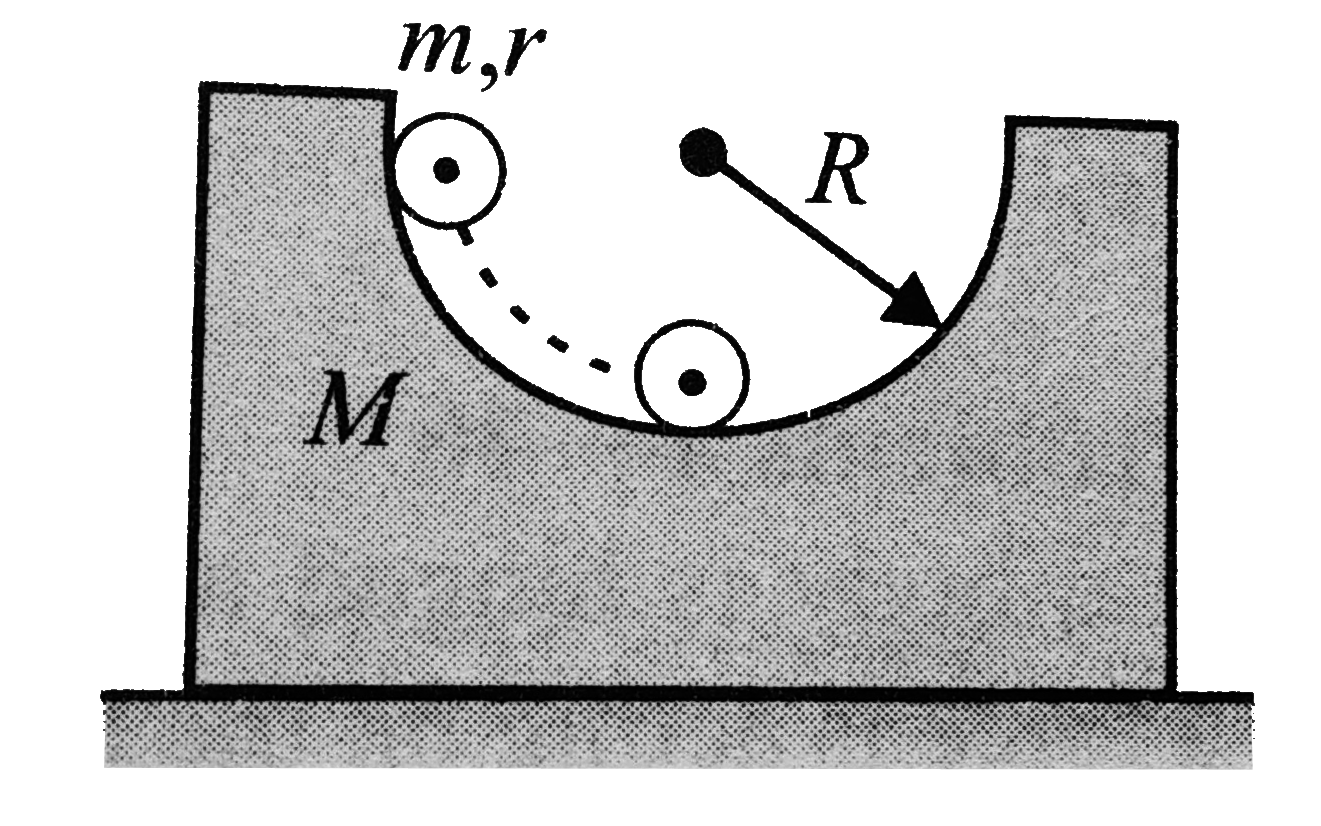
The speed of the point of contact of the cylinder with the block w.r.t. ground, when the cylinder reaches the bottom of the track is
View SolutionA block of mass m is released from a wedge of mass m as shown in figure . Find the time taken by the block to reach the end of the wedge.
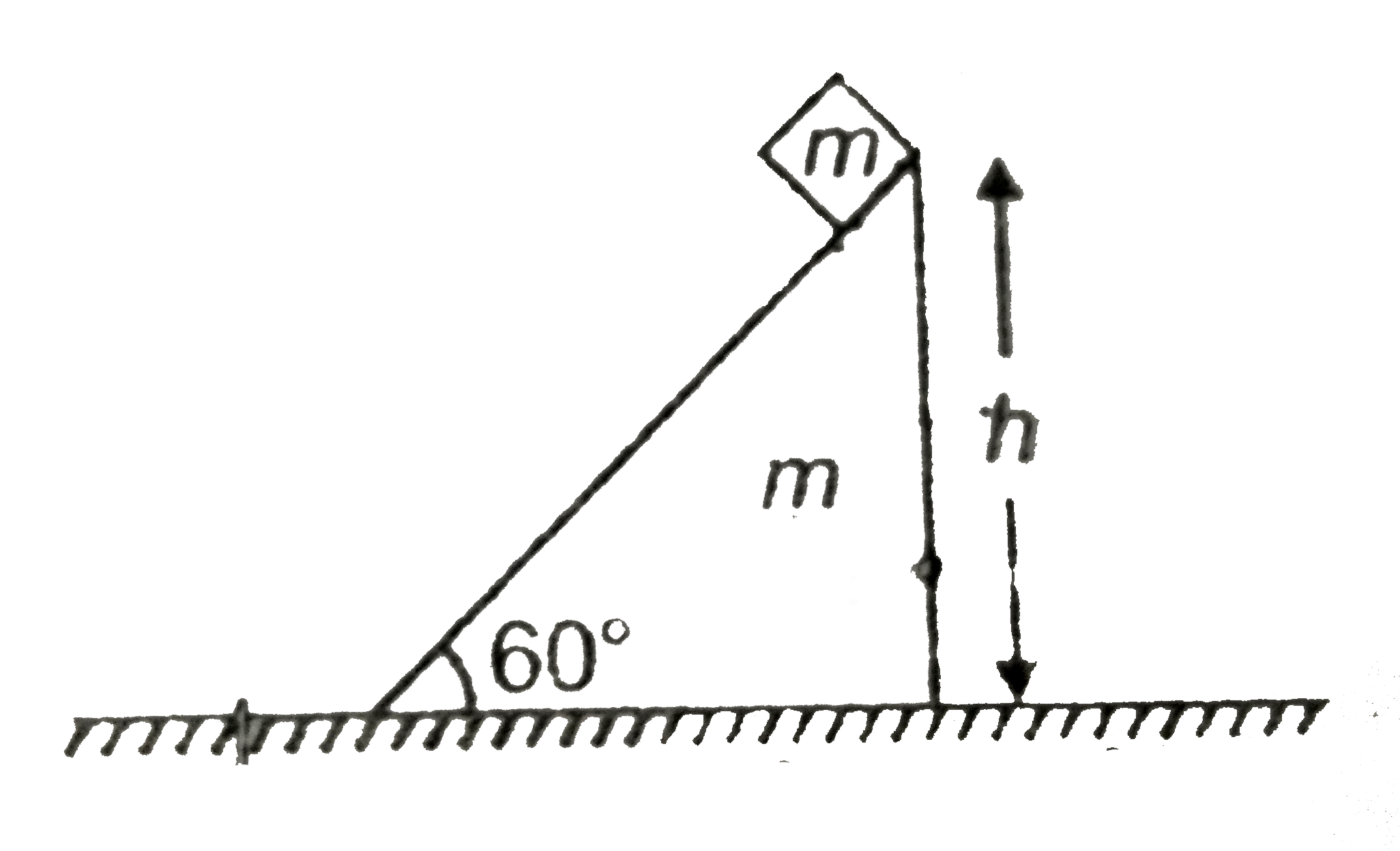
View SolutionA block of mass m slides down on inclined wedge of same mass m as shown in figure . Friction is absent everywhere . Acceleration of centre of mass of the block and wedge is
View Solution