A small head of m is pleced in the bottom of which glass of value radius R It is displaced by (h<<R) along the glass surface and released calculate the total distance described by it before it comes to rst of the botom μ is the coefficient of friction between bead and the watch glass
h/μ
h/2μ
h√μ
hμR
The correct Answer is:A
Since gravity is a cosrevation force work done by it depends only on the iniitial and final position and not on the length of the path .But work done by friction depends in the length of path as it is non consrvative
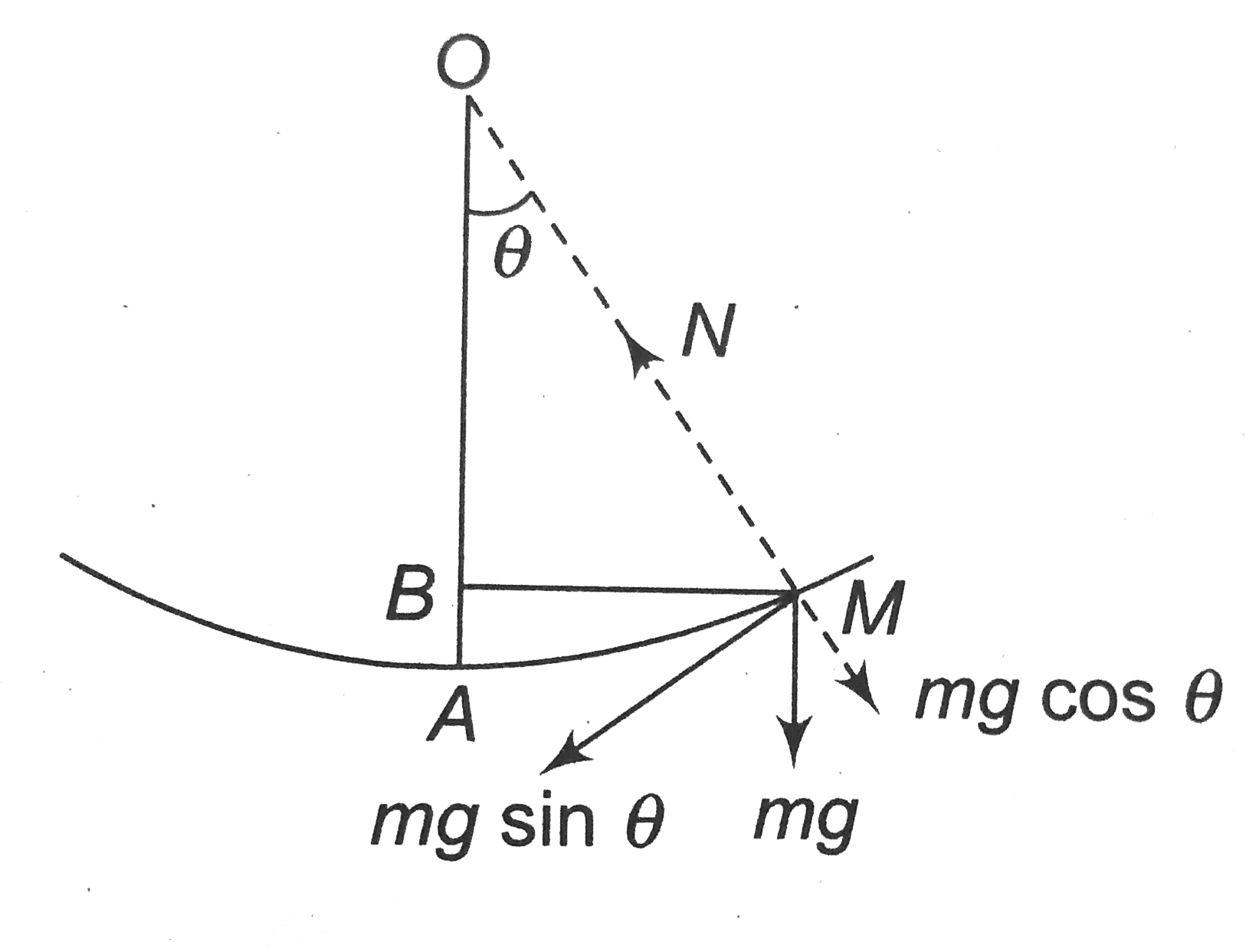
Wmg=mgh
Here N=mgcosθ=mg(∵θissmall)
Ffriction=μN=μmg
Work done by the friction =−μ mgs, where s is the length of path
mgh−μmgs=0 (zero because final kinetic energy is zero and initial energy is also zero)
∴s=hμ
Topper's Solved these Questions
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Potential Energy, Conservative And Non-Conservative Forces
28 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Conservation Of Mechanical Energy And Linear Momentum
24 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Chapter Test
29 Videos
- WAVES AND ACOUSTICSBOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Chapter Test
30 Videos
Similar Questions
A small ball of mass m=1 g is placed at the bottom of a watch glass of radius R=1 m. It is displaced by h=1 cm along the glass surface and released. Calculate the total distance deseribed by it before it comes to rest at the bottom, if μ=0.1 is the coefficient of friction between the ball and the watch glass.
View SolutionA point A is located on the rim of a wheel of radius R which rolls witout slipping along a horizontal surface witih velocity V. Find the total distance traversed by the point A between successive moments at which it touches the surface.
View Solution
Knowledge Check
A points is A located on the rim of a wheel of radius R which rolls without slipping along a horizontal surface with velocity v. The total distance travelled by the point A between successive moments at which it touches the surface is :
A4RB2RC8RD√8RA skier slides horizontally along the snow for a distance of 21 m before coming to rest. The coefficient of kinetic friction between the stier and the snow is μk=0.050. Initially, how fast was the skier going ?
A6.4m/sB4.5m/sC2.7m/sD5.4m/s
A tunnel is dug along a chord of Earth having length √3R where R is radius of Earth. A small block is released in the tunnel from the surface of Earth. The particle comes to rest centre of tunnel. If the coefficient of friction between the block and the surface of tunnel is μ=2√3n, then find n. Ignore the effect of rotation of Earth.
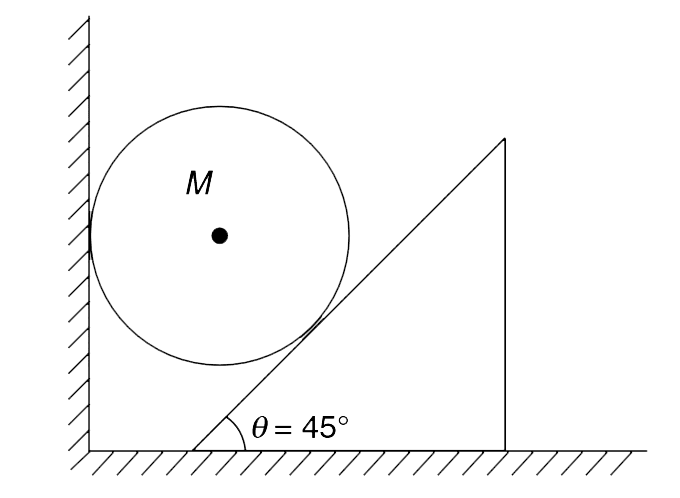
View SolutionA ball of mass M is in equilibrium between a vertical wall and the inclined surface of a wedge. The inclination of the wedge is θ=45∘ and its mass is very small compared to that of the ball. The coefficient of friction between the wedge and the floor is μ and there is no friction elsewhere. Find minimum value of μ for which this equilibrium is possible
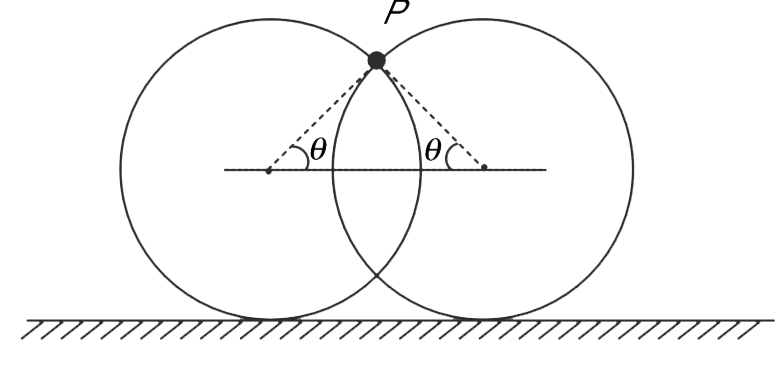
View SolutionTwo identical rings, each of mass M and radius R, are standing on a rough horizontal surface. The rings overlap such that the horizontal line passing through their centre makes an angle of θ=45∘ with the radius through their intersection point P. A small object of mass m is placed symmetrically on the rings at point P and released. Calculate the acceleration of the centre of the ring immediately after the release. There is no friction between the small object and the rings. The friction between the small object and the rings, and the friction between the rings and the ground is large enough to prevent slipping.
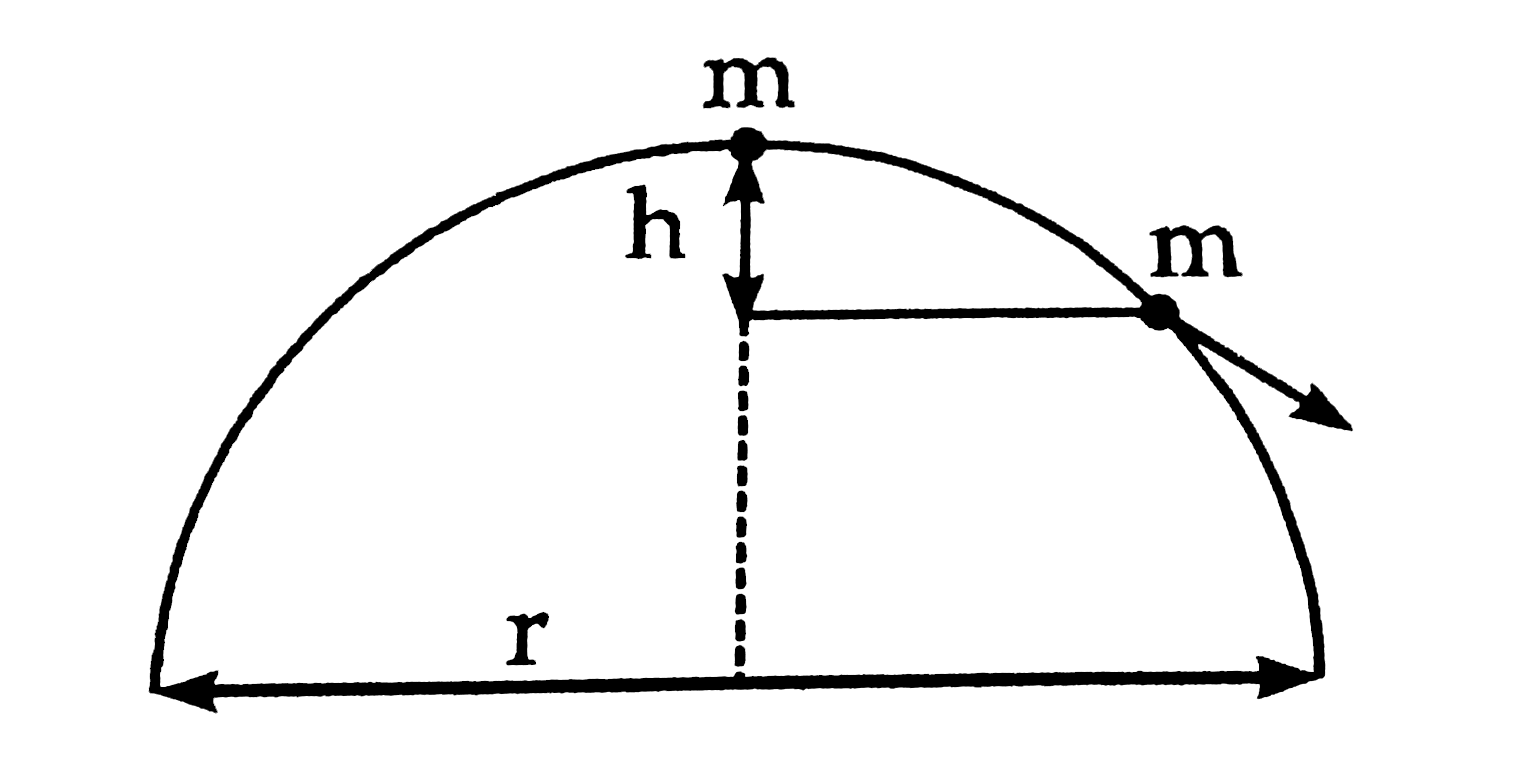
View SolutionA small body of mass m slide without friction from the top of a hemispherical cup of radius r as shown in figure. If leaves the surface to the cup at vertial distance h below the highest point then
View SolutionA tunnel is dug along a chord of Earth having length √3R is radius of Earth. A small block is released in the tunnel from the surfasce of Earth. The particle comes to rest at the centre of tunnel. Find coefficient of friction between the block and the surface of tunnel. Ignore the effect of rotation of Earth.
View SolutionIn the figure shown, a solid sphere of mass 'm' and radius r is released from a height 6r to slide down a smooth surface. A plank of same mass 'm' touches the horizontal portion of the surface at the ground. The co-efficient of friction between the plank and the sphere is μ and that between the plank and the ground is μ/4. Find the work done by the friction force between the plank and the ground till the sphere starts pure rolling on the plank. Neglect the height of the plank.

View Solution
