A small hole is made in a disc of mass M and radius R at a distance R/4 from centre. The disc is supported on a horizontal peg through this hole. The moment of inertia of the disc about horizontal peg is
MR29
516MR2
916MR2
54MR2
The correct Answer is:C
To find the moment of inertia of a disc about a horizontal peg located at a distance R4 from the center, we can follow these steps:
Step 1: Identify the moment of inertia of the disc about its center
The moment of inertia Icm of a solid disc about its center of mass is given by the formula:
Icm=12MR2
where M is the mass of the disc and R is its radius.
Step 2: Apply the Parallel Axis Theorem
The Parallel Axis Theorem states that the moment of inertia about any axis parallel to an axis through the center of mass is given by:
I=Icm+Md2
where d is the distance from the center of mass to the new axis.
Step 3: Determine the distance d
In this case, the distance d is R4 (the distance from the center of the disc to the peg).
Step 4: Substitute the values into the Parallel Axis Theorem
Now we can substitute the values into the formula:
I=12MR2+M(R4)2
Step 5: Calculate Md2
Calculating Md2:
Md2=M(R4)2=M⋅R216=MR216
Step 6: Combine the terms
Now substituting back:
I=12MR2+MR216
To combine these fractions, we need a common denominator:
I=816MR2+116MR2=916MR2
Final Answer
Thus, the moment of inertia of the disc about the horizontal peg is:
I=916MR2
---
The moment of inertia Icm of a solid disc about its center of mass is given by the formula:
Icm=12MR2
where M is the mass of the disc and R is its radius.
The Parallel Axis Theorem states that the moment of inertia about any axis parallel to an axis through the center of mass is given by:
I=Icm+Md2
where d is the distance from the center of mass to the new axis.
In this case, the distance d is R4 (the distance from the center of the disc to the peg).
Now we can substitute the values into the formula:
I=12MR2+M(R4)2
Calculating Md2:
Md2=M(R4)2=M⋅R216=MR216
Now substituting back:
I=12MR2+MR216
To combine these fractions, we need a common denominator:
I=816MR2+116MR2=916MR2
Thus, the moment of inertia of the disc about the horizontal peg is:
I=916MR2
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Linked Comprehension
28 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective
13 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
The moment of inertia of a disc of mass M and radius R about a tangent to its rim in its plane is
View SolutionA uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is

View SolutionA uniform disc (of mass M and radius a) has a hole (of radius b) drilled through it. The centre of the hole is at a distance c from the centre of the original disc. What is the moment of inertia of the disc about an axis through the centre of the disc and perpendicular to its plane ?
View SolutionMoment of inertia of a disc about an axis parallel to diameter and at a distance x from the centre of the disc is same as the moment of inertia of the disc about its centre axis. The radius of disc is R. The value of x is
View SolutionGiven a uniform disc of mass M and radius R. A small disc of radius R/2 is cut from this disc in such a way that the distance between the centres of the two discs is R/2. Find the moment of inertia of the remaining disc about a diameter of the original disc perpendicular to the line connecting the centres of the two discs
View SolutionA disc of mass M and radius R as shown in figure has some points on it. C is the cenre of disc, AB is the chord and O is mid point of chord. The notation IA means moment of inertia of the disc about axis passing through point A and pependicular to the plane of disc. Choose the correct option(s)
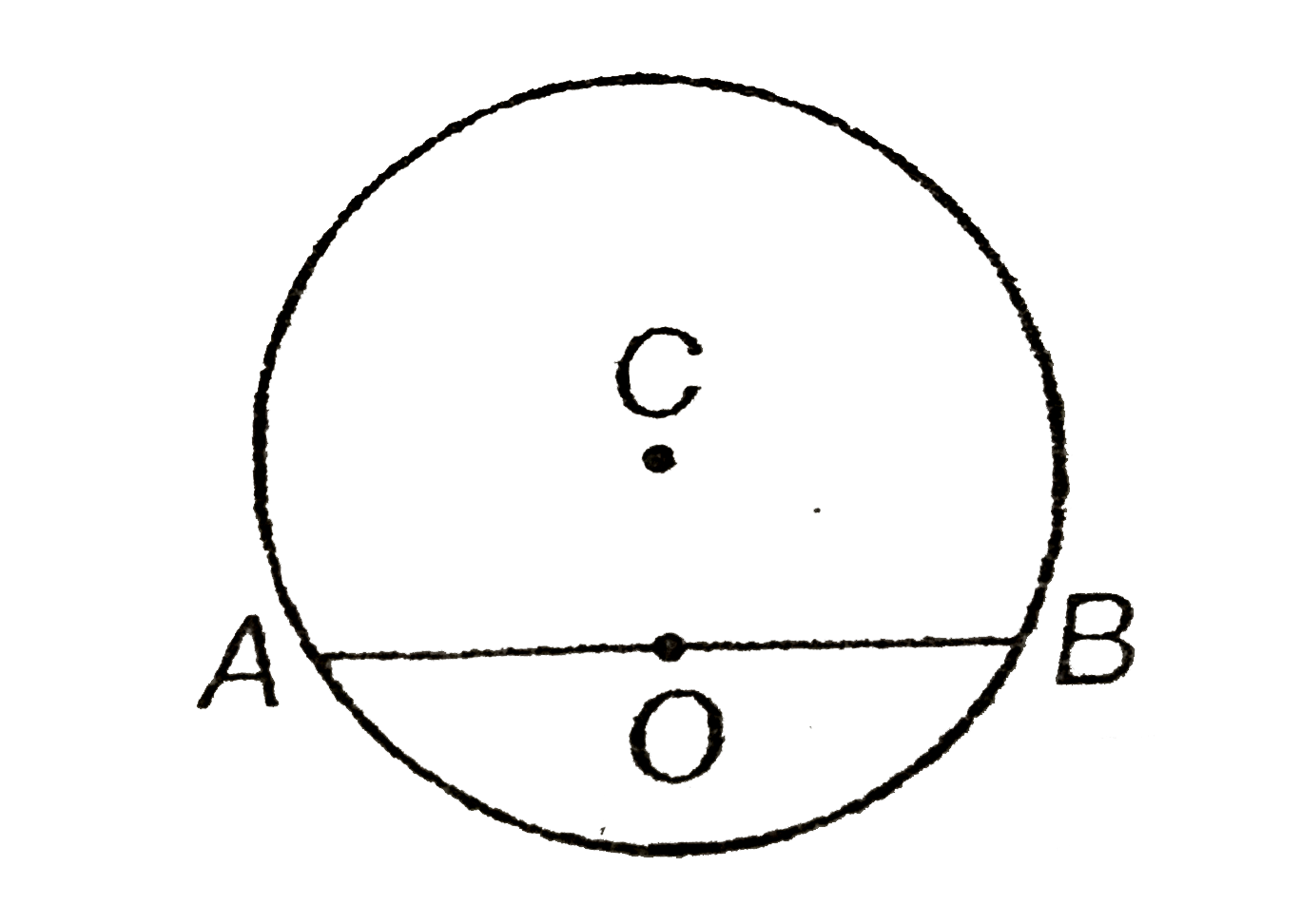
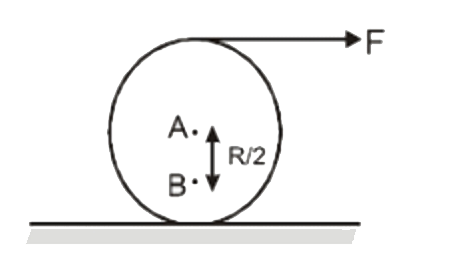
View SolutionA disc of mass m and radius R, is placed on a smooth text service fixed surface . Point A is the geometrical centre of the disc while point B is the centre of mass of the disc . The moment of inertia of the dics about an axis through its centre of mass and perpendicular to the plane of the figure is I .A constant force F is applied to the top of the disc . The acceleration of the centre A of the disc at the instant B is below A (on the same vertical line ) will be :
View SolutionA uniform disc of mass m and radius R has an additional rim of mass m as well as four symmetrically placed masses, each of mass m/4 tied at positions R/2 from the centre as shown in Fig. What is the total moment of inertia of the disc about an axis perpendicular to the disc through its centre?

View SolutionThe moment of inertia of a disc of mass M and radius R about an axis. Which is tangential to sircumference of disc and parallel to its diameter is.
View SolutionA disc of mass m and radius R has a concentric hole of radius r. Its moment of inertia about an axis through its center and perpendicular to its plane is
View Solution
