A small loop of area 3.1 mm2 is placed inside a long solenoid that has 672 turns/cm and carries a sinusoidally varying current i of amplitude 1.28 A and angular frequency 212 rad/s. The central axes of the loop and solenoid coincide. What is the amplitude of the emf induced in the loop?
To solve the problem of finding the amplitude of the emf induced in a small loop placed inside a long solenoid, we can follow these steps:
Step 1: Identify the given values
- Area of the loop, A=3.1mm2=3.1×10−6m2
- Number of turns per unit length of the solenoid, n=672turns/cm=67200turns/m
- Amplitude of current, I0=1.28A
- Angular frequency, ω=212rad/s
Step 2: Calculate the magnetic field inside the solenoid
The magnetic field B inside a solenoid is given by the formula:
B=μ0nI
where μ0=4π×10−7T m/A is the permeability of free space.
Substituting the values:
B=(4π×10−7)×(67200)×(I0)
Since I varies sinusoidally, we will use the amplitude I0:
B=(4π×10−7)×(67200)×(1.28)
Step 3: Calculate the magnetic field value
Calculating B:
B=(4π×10−7)×(67200)×(1.28)≈0.000337T(approximately)
Step 4: Calculate the magnetic flux Φ
The magnetic flux Φ through the loop is given by:
Φ=B⋅A
Substituting the values:
Φ=0.000337×3.1×10−6
Calculating Φ:
Φ≈1.0437×10−9Wb
Step 5: Calculate the induced emf E
The induced emf E is given by Faraday's law of electromagnetic induction:
E=−dΦdt
For sinusoidal variation, we can express this as:
E=ωΦ
Substituting the values:
E=ω⋅(B⋅A)=212⋅(1.0437×10−9)
Step 6: Calculate the final value of induced emf
Calculating E:
E≈2.21×10−7V=221nV
Final Answer
The amplitude of the emf induced in the loop is approximately 221nV.
---
- Area of the loop, A=3.1mm2=3.1×10−6m2
- Number of turns per unit length of the solenoid, n=672turns/cm=67200turns/m
- Amplitude of current, I0=1.28A
- Angular frequency, ω=212rad/s
The magnetic field B inside a solenoid is given by the formula:
B=μ0nI
where μ0=4π×10−7T m/A is the permeability of free space.
B=(4π×10−7)×(67200)×(I0)
Since I varies sinusoidally, we will use the amplitude I0:
B=(4π×10−7)×(67200)×(1.28)
Calculating B:
B=(4π×10−7)×(67200)×(1.28)≈0.000337T(approximately)
The magnetic flux Φ through the loop is given by:
Φ=B⋅A
Substituting the values:
Φ=0.000337×3.1×10−6
Calculating Φ:
Φ≈1.0437×10−9Wb
The induced emf E is given by Faraday's law of electromagnetic induction:
E=−dΦdt
For sinusoidal variation, we can express this as:
E=ωΦ
Substituting the values:
E=ω⋅(B⋅A)=212⋅(1.0437×10−9)
Calculating E:
E≈2.21×10−7V=221nV
The amplitude of the emf induced in the loop is approximately 221nV.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)
45 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type)
13 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHECKPOINTS
9 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type
1 Videos
- ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT EXERCISE - Practice Questions (Integer)
7 Videos
Similar Questions
Figure shows a square current carrying loop ABCD of side 2m and currenti=12A. The magnetic moment →M of the loop is

View SolutionAn air cored solenoid of length 50 cm and area of cross section 20m2 has 200 turns and carries a current of 5.0 A. On switching off, the current decreases to across the ends of the solenoid.
View Solution
Knowledge Check
A small, conducting circular loop is placed inside a long solenoid carrying a current. The plane of the loop contains the axis of the solenoid. If the current in the solenoid is varied, the current induced in the loop is
AclockwiseBanti-clockwiseCzeroDclockwise or anti-clockwise depending on whether the resistance is increased or decreasedA long solenoid has 20 turns per cm and carries a current i. the magnetic field at its centre is 6.28×10−2Wb/m2. Another long solenoid has 100 turns per cm and it carries a current i/3 . The value of the magnetic field at its centre is
A1.05×10−4Wb/m2B1.05×10−2Wb/m2C1.−5×10−5Wb/m2D1.05×10−6Wb/m2A single conducting loop with an area of 2.0 m2 rotates in a uniform magnetic field so that the induced emf has a sinusoidal time dependence as shown.
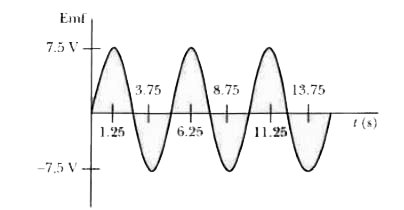
With what angular frequency does the loop rotate?A0.16 rad/sB0.52 rad/sC1.26 rad/sD0.30 rad/s
A long solenoid with 1.5 turns per cm has a small loop of area 2.0cm2 placed inside the solenoid normal to its axis. If the current in the solenoid changes steadily from 2.0A to 4.0A in 1.0s. The emf induced in the loop is
View SolutionA rectangular loop (area = 0.15 m2) turns in a uniform magnetic field, B = 0.20 T. When the angle between the field and the normal to the plane of the loop is π/2 rad and increasing at 0.60 rad/s, what emf is induced in the loop?
View SolutionA solenoid coil of 300turns/m is carrying a current of 5A. The length of the solenoid is 0⋅5m and has a radius of 1cm. Find the magnitude of the magnetic field well inside the solenoid.
View SolutionA long solenoid has 200turnspercm and carries a current i. The magnetic field at its centre is 6.28×10−2weber/cm2. Another long soloenoid has 100turnspercm and it carries a current i3. The value of the magnetic field at its centre is
View SolutionA long solenoid has 200 turns per cm and carries a current 1. The magnetic field at its centre is 6.28×10−2Wbm−2. Another long solenoid has 100 turns per cm and it carries a current 7/3. The value of the magnetic field at its centre is
View Solution
