A smooth spehre of radius R is made to translate oin a straight line with a constant acceleration a. A particle kept on the top of the sphere is released rom there at zero velocity with respect to the sphere. Find the speed of the particle with respect to the sphere as a functon of the angle it slides.
The situation is shown in figure. As the sphere is accelerating, it becomes a non-inertial frame for the particle and when particle is displaced, pseudo force acting on it will also do work in addition to gravity and will cause increment in its kinetic energy.
Using work-energy theorem at points A and B, we have
or

Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.5
15 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Subjective
23 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.3
26 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A smooth sphere of radius R is moving in a straight line with an acceleration a. A particle is released from top of the sphere from rest. Find the speed of the particle when it is at an angular position θ from the initial position relative to the sphere.
View SolutionA hemisphere of radius R and of mass 4m is free to Slide with its base on a smooth horizontal table. A particle mass m is placed on the top of the hemisphere. Find the angular velocity of the particle relative to hemisphere at an angular displacement θ when velocity of hemisphere has become v.

View Solution
Knowledge Check
A smooth spehre of radius R is made to translate oin a straight line with a constant acceleration a. A particle kept on the top of the sphere is released rom there at zero velocity with respect to the sphere. Find the speed of the particle with respect to the sphere as a functon of the angle θ it slides.
A√Rg(sinθ+cosθ)2B√Rg(1+cosθ−sinθ)C√4RgsinθD√2Rg(1+sinθ−cosθ)A particle of mass m is kept at the top of a smooth fixed sphere. It is given a horizontal velocity v then:
Ait will start moving along a circular path if v<√gRBit will start moving along a circular path if v>√gRCit will start moving along a parabolic path if v<√gRDit will start moving along a parabolic path if v>√gRInside a smooth hemispherical cavity, a particle P can slide freely. The block having this cavity is moving with constant acceleration a = g (where g is acceleration due to gravity). The particle is released from the state of rest from the topmost position of the surface of the cavity as shown. The angle θ with the vertical, when the particle will have maximum velocity with respect to the block is
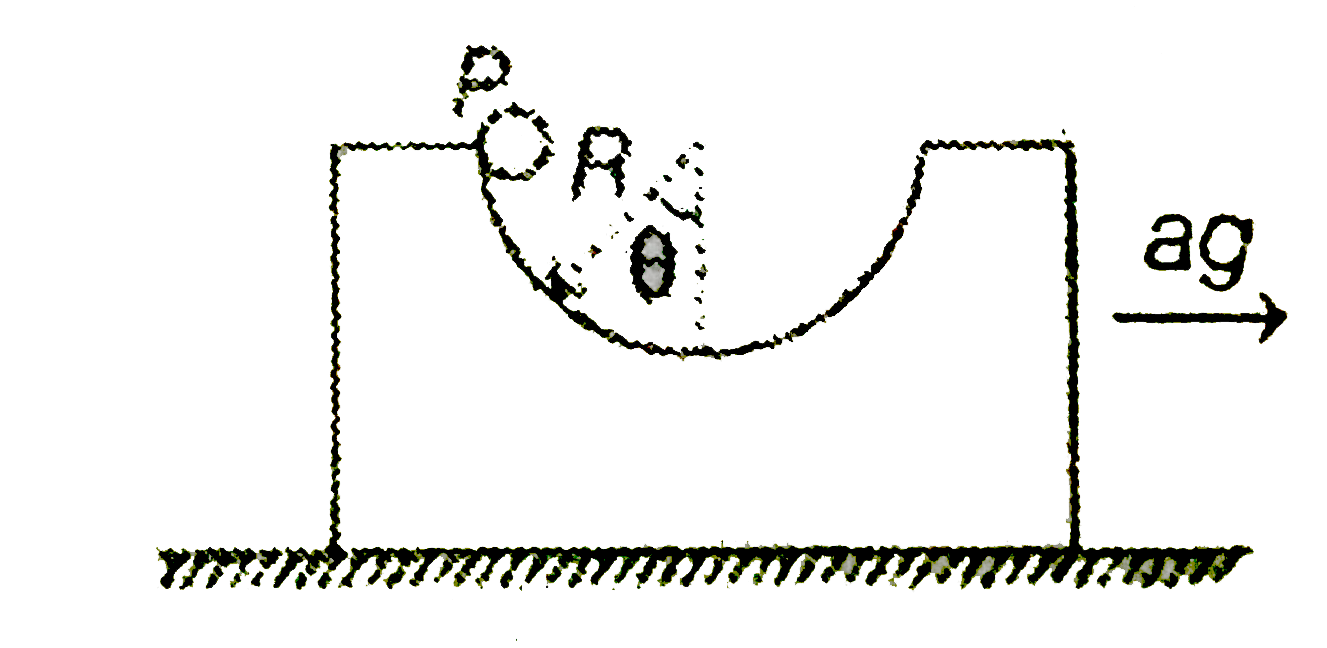 A45∘B60∘C30∘D0∘
A45∘B60∘C30∘D0∘
A particle slides on the surface of a fixed smooth sphere starting from the topmost pont. Find the angle rotated by the radius through the particle, when it leaves contact with the sphere.
View SolutionA small body is placed on the top of a smooth sphere of radius R. Then the sphere is imparted a constant acceleration w0 in the horizontal direction and the body begins sliding down. Find:
(a) the velocity of the body relative to the sphere at the moment of break-off,
(b) the angle θ0 between the vertical and the radius vector drawn from the centre of the sphere to the break-off point, calculate θ0 for w0=g.
View SolutionA particle of mass m is kept on a fixed , smooth sphere of radius R at a position, where the rdius thrugh the particle makes an angle of 300 with the vertical. The particle is releases from this positon. a. What is the force exerted by the sphere on teh particle just after the release? b. Find the distance travelled by the particle before it leaves contact with the sphere.
View SolutionAS chain of length l and mass m lies o the surface of a smooth sphere of radius R>l with one end tied to the top of the sphere. a.Find the gravitational potential energy of the chain with reference level at the centre of the sphere. B. suppose the chin is released and slides down the sphere. Find the kinetic eneergy of the chain, when it has slid through an angle θ c. find the tangential acceleration dvdt of the chain when the chain starts sliding down.
View SolutionA particle moving on the inside of a smooth sphere of radius r describing a horizontal circle at a distance r/2 below the centre of the sphere. What is its speed ?
View Solution
