A smooth sphere of radius R is made to translate line with a constant acceleration a=g. A particle kept on the top of the sphere is released from there at zero velocity with respect to the sphere. Find the speed of the particle with respect to the sphere as a function of angle θ as it slides down.
The situation is shown in figure. As the sphere is accelerating, it becomes a non-inertial frame for the particle and when particle is displaced, pseudo force acting on it will also do work in addition to gravity and will cause increment in its kinetic energy.
Using work-energy theorem at points A and B, we have
0+mgR(1−cosθ)+maRsinθ=12mv2
or v=√R{asinθ+g(1−cosθ)]

Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.5
15 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Subjective
23 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.3
26 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A smooth sphere of radius R is made to translate oin a straight line with a constant acceleration a. A particle kept on the top of the sphere is released rom there at zero velocity with respect to the sphere. Find the speed of the particle with respect to the sphere as a function of the angle θ it slides.
View SolutionA smooth chute is made in a dielectric sphere of radius R and uniform volume charge density. ρ. A charge particle of mass m and charge -q is placed at the centre of the sphere. Find the time period of motion of the particle?

View Solution
Knowledge Check
A particle rests on the top of a hemishpere of radius R. Find the smallest horizontal velocity that must be imparted to the particle if it is yo leave the hemisphere without sliding down it.
A√gRB√2gRC√3gRD√5gR
A particle of mass m is kept on a fixed, smooth sphere of radius R at a position, where the radius through the particle makes an angle of 30 ∘ with the vertical. The particle is released from this position. (a) What is the force exerted by the sphere on the particle just after the release? (b) Find the distance traveled by the particle before it leaves contact with the sphere.
View SolutionA particle of mass m starts to slide down from the top of the fixed smooth sphere. What is the tangential acceleration when it break off the sphere ?
View SolutionA solid sphere of radius R is resting on a smooth horizontal surface. A constant force F is applied at a height h from the bottom. Choose the correct alternative.

View SolutionA particle is projected with velocity u horizontally from the top of a smooth sphere of radius a so that it slides down the outside of the sphere. If the particle leaves the sphere when it has fallen a height a4 , the value of u is
View SolutionA sphere is released on a smooth inclined plane from the top. When it moves down, its angular momentum is
View SolutionA ball is kept at a height h above the surface of a heavy transparent sphere made of a material of refractive index The radius of the sphere is R. At t = 0, the ball is dropped to fall normally on the sphere. Find the speed of the image formed as a function of time for t<√2hg. Consider only the image by a single refraction.
View SolutionA uniformly charged sphere of charge Q and radius R is placed at some height from ground surface and sphere is fixed. Now a charged particle of mass m and charge q is released form rest just below to sphere what will be speed of particle after travelling Y-direction
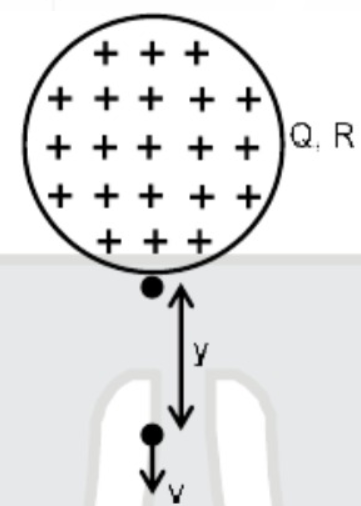
View Solution
