A solid at temperature T1 is kept in an evacuated chamber at temperature T2>T1 . The rate of increase of temperature of the body is proportional to
t42−t41
(t24+273)−(t41+273)
t2−t1
t22−t21
The correct Answer is:C
c) As we know that, the rate of cooling is
dthηdt=bA(θ−θ0)
where, bA=constant
⇒dthηdtα(θ−θ0)
Also −dTdtαT−T0
where, T=temperature and t=time
So, the rate of heat absorbed by cooled body is proportional to t2−t1.
Topper's Solved these Questions
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Match the columns
4 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 Subjective
14 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
Similar Questions
A solid at temperature T1 is kept in an evacuated chamber at temperature T2>T1 . The rate of increase of temperature of the body is propertional to
View SolutionA copper block of mass 'm' at temperature 'T1' is kept in the open atmosphere at temperature 'T2' where T2>T1. The variation of entropy of the copper block with time is best illustrated by
View Solution
Knowledge Check
Two bars of same length and same cross-sectional area but of different thermal conductivites K1 and K2 are joined end to end as shown in the figure. One end of the compound bar it is at temperature T1 and the opposite end at temperature T2 (whereT1>T2). The temperature of the junction is
 AK1T1+K2T2K1+K2BK1T2+K2T1K1+K2CK1(T1+T2)K1+K2DK2T1+T2K1
AK1T1+K2T2K1+K2BK1T2+K2T1K1+K2CK1(T1+T2)K1+K2DK2T1+T2K1
One end of a rod of length L and crosssectional area A is kept in a furnace at temperature T1. The other end of the rod is kept at a temperature T2. The thermal conductivity of the matrieal of the rod is K and emissivity of the rod is e. It is gives that T!=Ts+ΔT, where ΔT<<Ts,Ts is the temperature of the surroundings. If ΔT∝(T1−T2) find the proportional constant, consider that heat is lost only by rediation at the end where the temperature of the rod is T1.

View SolutionA solid copper sphere of density ρ, specific heat c and radius r is at temperature T1. It is suspended inside a chamber whose walls are at temperature 0K. What is the time required for the temperature of sphere to drop to T2? Take the emmissivity of the sphere to be equal to e.
View SolutionA solid sphere of radius 'R' density ρ and specific heat 'S' initially at temperature T0 Kelvin is suspended in a surrounding at temperature 0K. Then the time required to decrease the temperature of the sphere from T0 to T02 kelvin is (Assume sphere behaves like a black body)
View SolutionOne end of rod of length L and cross-sectional area A is kept in a furance of temperature T1. The other end of the rod is kept at at temperature T2. The thermal conductivity of the material of the rod is K and emissivity of the rod is e. It is given that T2=TS+ΔT where ΔT<<TS, TS being the temperature of the surroundings. If ΔT∝(T1−TS), find the proportionality constant. Consider that heat is lost only by radiation at the end where the temperature of the rod is T2.
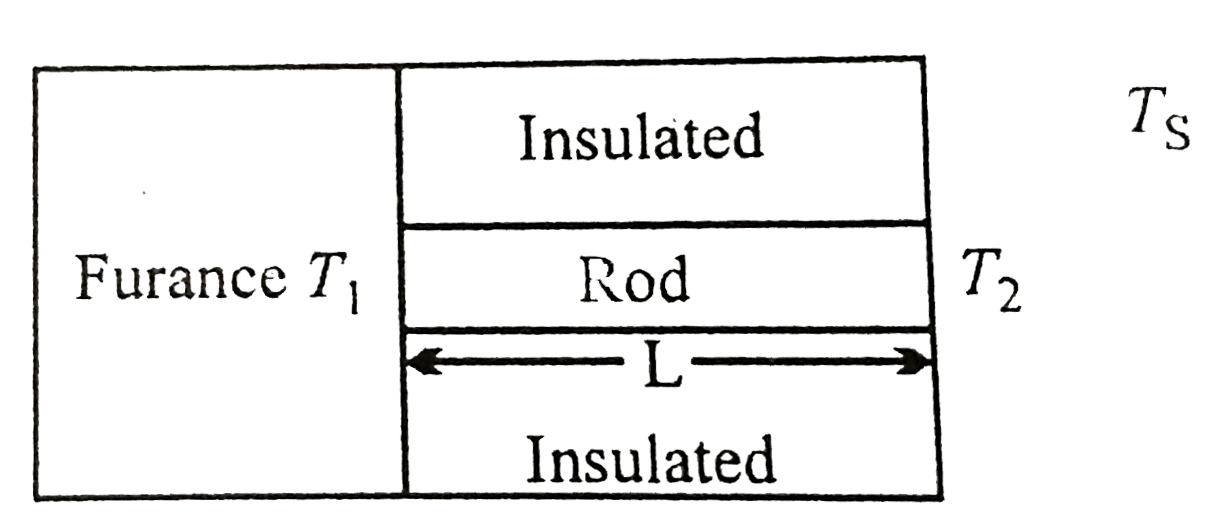
View SolutionThe ends of a metal rod are kept at temperatures θ1 and θ2 with θ2>θ1. The rate of flow of heat along the rod is directly proportional to
View SolutionThree Carnot engines operate in series between a heat source at a temperature T1 and a heat sink at temperature T4 (see figure). There are two other reservoirs at temperature T2andT3, as shown, with T1>T2>T3>T4. The three engines are equally efficient if :

View SolutionA black body of temperature T is inside a chamber of temperature T0 Now the closed chamber is slightly opened to Sun that temeperature of black body (T) and chamber (T0) remain constant .
View Solution
