on observing light form three different stars P, Q and R, it was found that intensity of violet colour is maximum in the spectrum of P, the intensity of green colour is maximum in the spectrum of R and the intensity of red colour is maximum in the spectrum of Q. If Tp,TQ and TR are the respective absolute temperatures of P, Q and R, then it can be concluded from the above observation that
TP>TQ>TR
TP>TR>TQ
TP<TR<TQ
TP<TQ<TR
The correct Answer is:B
b) We know from Wien's displacement law,
λmT=constant
So, Tα1λm
As, λr>λg>λv
So, Tr<Tg<Tv
Given, P→vmax,Q→rmax,R→gmax
Hence, TQ<TR<Tp
i.e, TP>TR>TQ
Topper's Solved these Questions
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Match the columns
4 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 Subjective
14 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
Similar Questions
On observing light from three different stars P, Q and R, it was found that intensity of violet colour is maximum in the spectrum of P, the intensity of green colour is maximum in the spectrum of R and the intensity of red colour is maximum in the spectrum of Q. if TP, TQ and TR are respective absolute temperature of P, Q and R. then it can be concluded from the above observation that
View SolutionThe temperature of a furnace is 2324∘C and the intensity is maximum in its radiation spectrum nearly at 12,000Å.If the intensity in the spectrum of star is maximum nearly at 4800Å , then the surface temperature of star is nearly:
View SolutionThe temperature of a furnace is 2324∘C and the intensity is maximum in its radiation spectrum nearly at 12000A . If the intensity in the spectrum of a star is maximum nearly at 4800A, calculate the surface temperature of the star.
View SolutionIf P,Q and R are three collinear points such that →PQ=→a and →QR = →b. Find the vector →PR .
View SolutionLet p,qandr be three statements, then (~p→q)→r is equivalent to
View SolutionIn Figure, PQ>PR.QS and RS are the bisectors of ∠Q and ∠R respectively. Prove that SQ>SR.
View SolutionIn Fig. , the side QR of △ PQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR=12∠QPR.
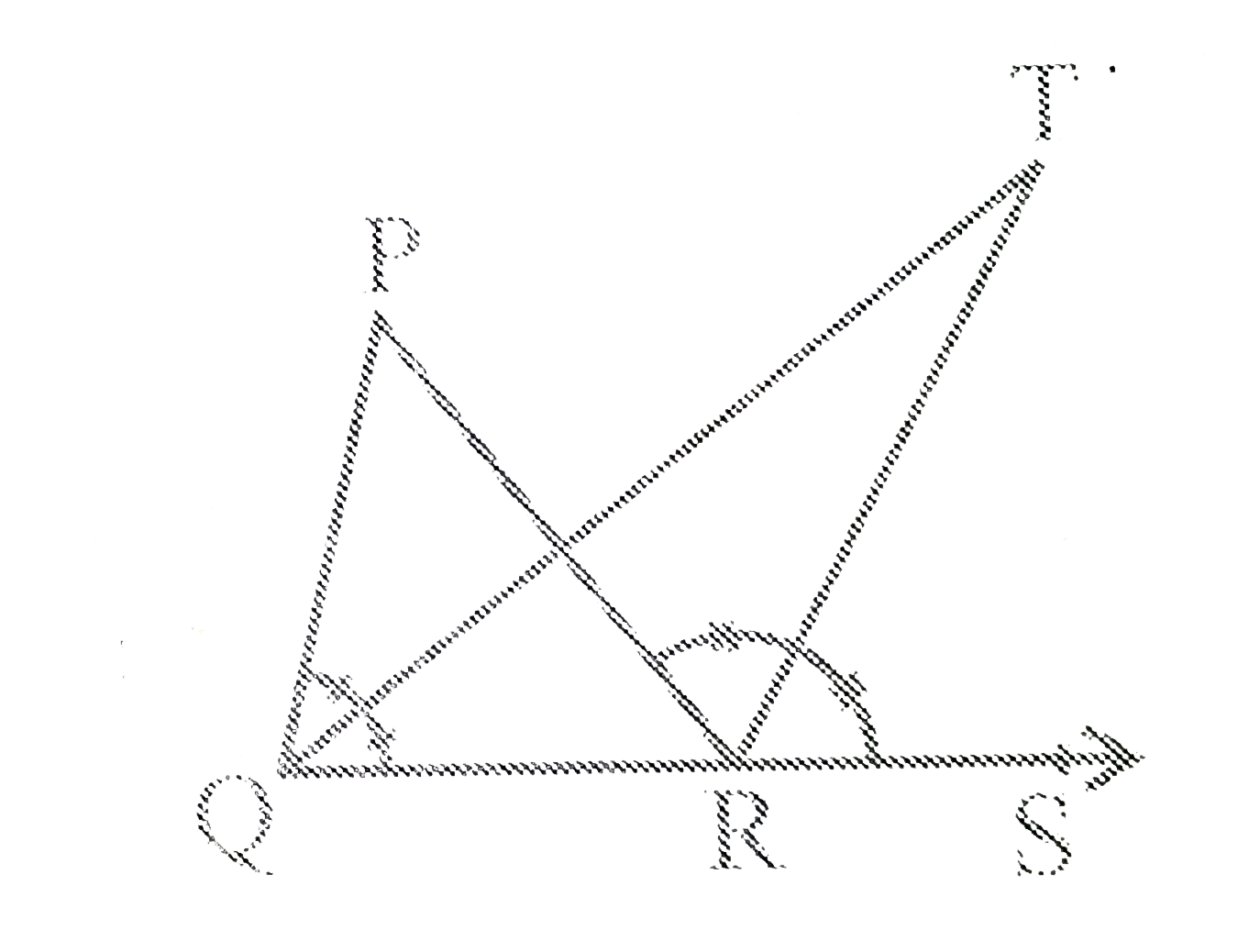
View SolutionThree forces P, Q and R are acting on a particel in the plane, the angle between P and Q and that between Q and R are 150∘ and 120∘ respectively. Then for equilibrium, forces P, Q and R are in the ratio
View SolutionThree forces P, Q and R are acting on a particel in the plane, the angle between P and Q and that between Q and R are 150∘ and 120∘ respectively. Then for equilibrium, forces P, Q and R are in the ratio
View SolutionIn Figure, S and T are points on the sides PQ and PR respectively of △PQR such that PT=2cm , TR=4cm and ST is parallel to QR . Find the ratio of the areas of △PST and △PQR .
View Solution
