A solid sphere is rolling on a horizontal surface such that speed of the centre of sphere is u. Mase of the sphere is m and radius R. Magnitude of angular momentum about the point of contact is found to be 7nmvR/. Find the value of n
The correct Answer is:5
To solve the problem, we need to find the value of n given that the angular momentum L about the point of contact of a rolling solid sphere is expressed as 7nmvR.
1. Understanding the System:
- We have a solid sphere rolling without slipping on a horizontal surface.
- The speed of the center of the sphere is u.
- The mass of the sphere is m and its radius is R.
2. Angular Momentum about the Point of Contact:
- The angular momentum L about the point of contact can be calculated using the formula:
L=R×P+Icmω
- Here, R is the position vector from the point of contact to the center of mass, P=mv is the linear momentum of the center of mass, Icm is the moment of inertia of the sphere about its center, and ω is the angular velocity.
3. Calculating Linear Momentum:
- The linear momentum P of the center of mass is:
P=mv
- Since the sphere is rolling, the speed v at the center of mass is u.
4. Calculating Moment of Inertia:
- The moment of inertia Icm for a solid sphere about its center is given by:
Icm=25mR2
5. Calculating Angular Velocity:
- The angular velocity ω is related to the linear speed u by:
ω=uR
6. Position Vector:
- The position vector R from the point of contact to the center of mass is equal to the radius R.
7. Calculating Angular Momentum:
- Substituting the values into the angular momentum formula:
L=R×mv+Icmω
- The first term becomes:
R \times mv = R \cdot mv \cdot \hat{k} \quad \text{(where \hat{k} is the unit vector perpendicular to the plane)}
- The second term becomes:
Icmω=25mR2⋅uR=25mRu
8. Combining Terms:
- The total angular momentum L about the point of contact is:
L=mvR+25mRu=mvR+25mvR=(1+25)mvR=75mvR
9. Finding n:
- According to the problem statement, the angular momentum is given as 7nmvR.
- Comparing both expressions:
75mvR=7nmvR
- Therefore, we can equate:
n=5
Final Answer:
The value of n is 5.
- We have a solid sphere rolling without slipping on a horizontal surface.
- The speed of the center of the sphere is u.
- The mass of the sphere is m and its radius is R.
- The angular momentum L about the point of contact can be calculated using the formula:
L=R×P+Icmω
- Here, R is the position vector from the point of contact to the center of mass, P=mv is the linear momentum of the center of mass, Icm is the moment of inertia of the sphere about its center, and ω is the angular velocity.
- The linear momentum P of the center of mass is:
P=mv
- Since the sphere is rolling, the speed v at the center of mass is u.
- The moment of inertia Icm for a solid sphere about its center is given by:
Icm=25mR2
- The angular velocity ω is related to the linear speed u by:
ω=uR
- The position vector R from the point of contact to the center of mass is equal to the radius R.
- Substituting the values into the angular momentum formula:
L=R×mv+Icmω
- The first term becomes:
R \times mv = R \cdot mv \cdot \hat{k} \quad \text{(where \hat{k} is the unit vector perpendicular to the plane)}
- The second term becomes:
Icmω=25mR2⋅uR=25mRu
- The total angular momentum L about the point of contact is:
L=mvR+25mRu=mvR+25mvR=(1+25)mvR=75mvR
- According to the problem statement, the angular momentum is given as 7nmvR.
- Comparing both expressions:
75mvR=7nmvR
- Therefore, we can equate:
n=5
The value of n is 5.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Chapter Practice Test (for Board Examination)16videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (MATRIX MATCH TYPE QUESTIONS) )1videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)6videos
PHYSICAL WORLD
- BOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST15videos
THERMAL PROPERTIES OF MATTER
Similar Questions
A thin ring of mass m and radius R is in pure rolling over a horizontal surface. If v0 is the velocity of the centre of mass of the ring, then the angular momentum of the ring about the point of contact is
View SolutionA sphere is rolling without slipping on a fixed horizontal plane surface. In the figure, A is the point of contact, B is the centre of the sphere and C is its topmost point. Then :
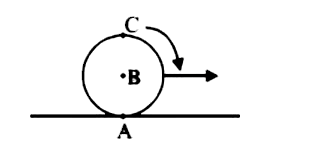 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A sphere of mass M rolls without slipping on rough surface with centre of mass has constant speed v0. If mass of the sphere is m and its radius be R, then the angular momentum of the sphere about the point of contact is.
A45Mv0R(−ˆk)B95Mv0R(−ˆk)C85Mv0R(−ˆk)D75Mv0R(−ˆk) - Question 2 - Select One
A uniform solid sphere rolls on a horizontal surface at 20 m/s. It, then, rolls up a plane inclined at
A16 mB20 mC28 mD36 m - Question 3 - Select One
A solid sphere rolling on a rough horizontal surface. Acceleration of contact point is zero.
A solid sphere can roll on the smooth surface.AStatement-1 is True, Statement-2 is Ture , Statement -2 is a correct explanation for statement -1.BStatement-1 is True, Statement-2 is True , Statement-2 is NOT a correct explanation fro Statement -1.CStatement-1 is True, Statement-2 is False.DStatement-1 is False, Statement-2 is True.
A sphere of radius R is rolling on a rough horizontal surface. The magnitude of velocity of A with respect to ground will be
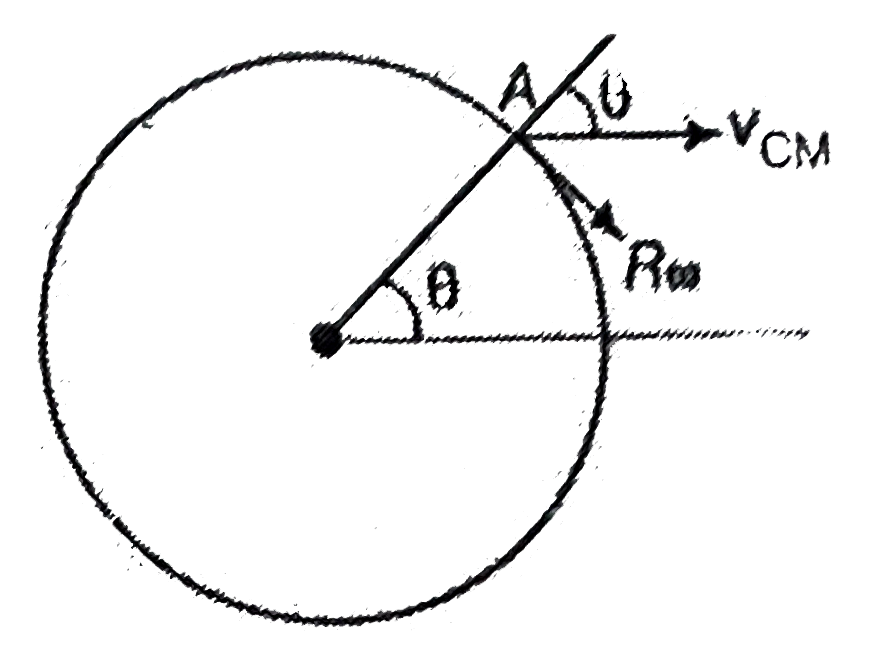 View Solution
View SolutionA solid sphere of radius r r is rolling on a horizontal surface. The ratio between the rotational kinetic energy and total energy.
View SolutionA sphere is rolling without slipping on a fixed horizontal plane surface. In the figure, A is the point of contact. B is the centre of the sphere and C is its topmost point. Then
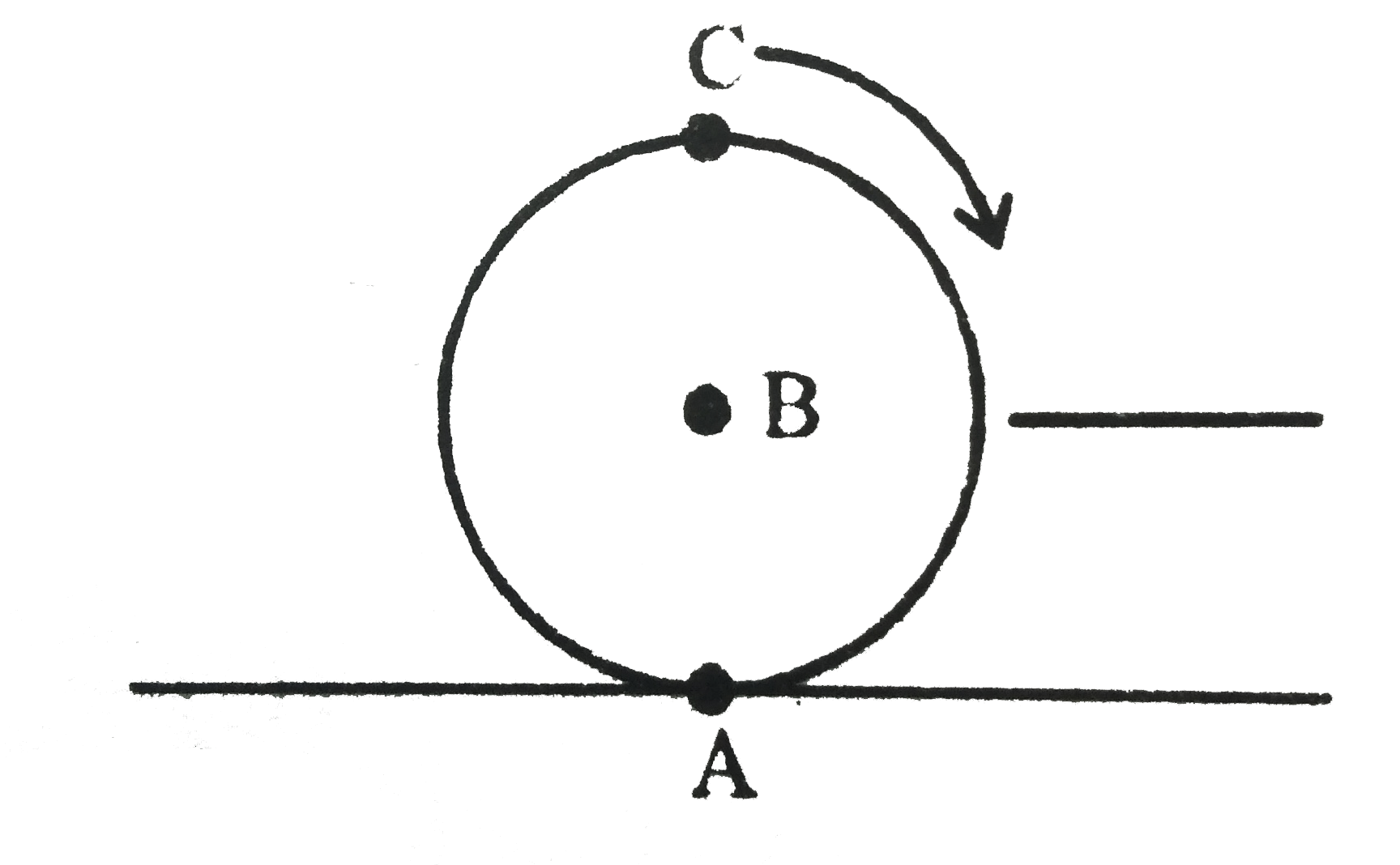 .View Solution
.View SolutionA sphere is rolling without slipping on a fixed horizontal plane surface. In the figure, A is the point of contact, B is the centre of the sphere and C is its topmost point. Then
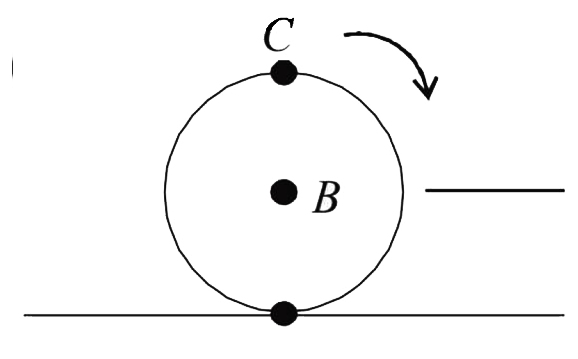 View Solution
View SolutionA solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that vc.m.=v0.
View Solution

