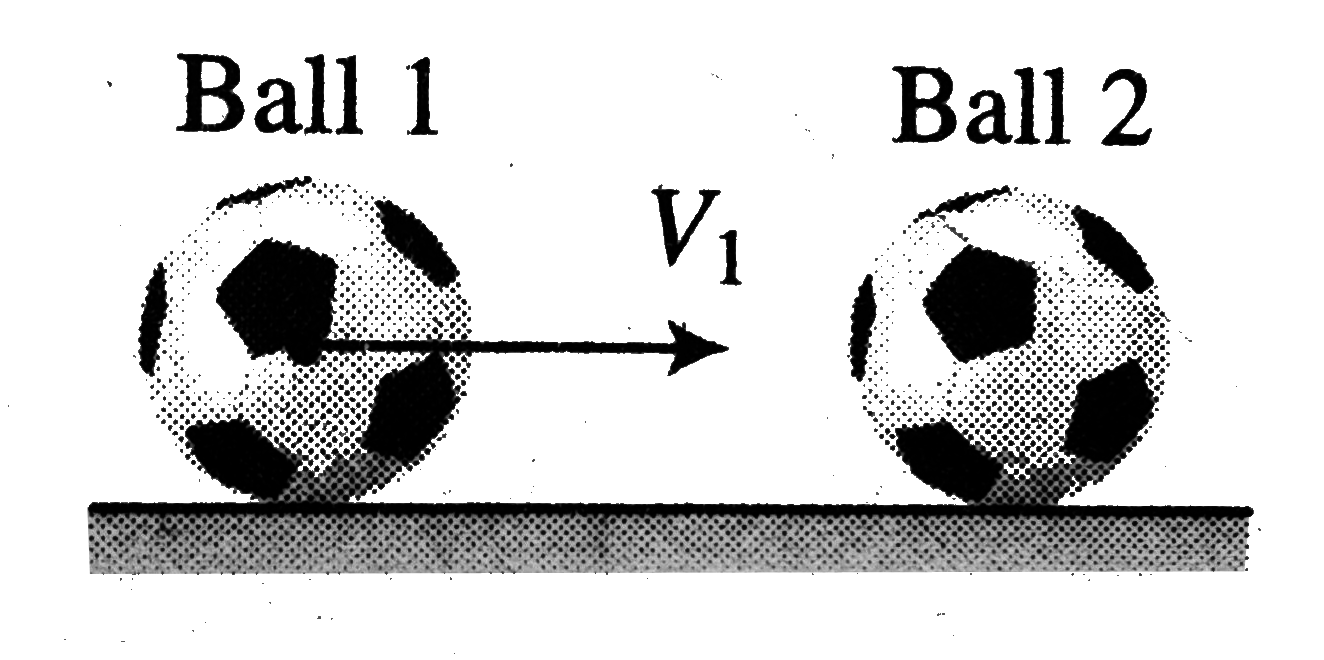
A solid spherical ball rolling without slipping collides elastically with an identical ball at rest, as shown in the figure. Assuming that the frictional forces are small enough to have negligible effect during the instant of collision, calculate, the velocity of each ball along enough time after the collision when each ball is again rolling without slipping.
The correct Answer is:57V
Before collision V1=V,V2=0

ω1=VR,ω2=0
During collision for forces pass through centre of each sphere and friction force is negligibly small so that the angular momentum about the centre of each ball is coserved.
Thus V′1=0,V′2=V1=0
With these linear and angular velocities start to move and eventually start sure rolling. The directions shown in the figure are considered to be positive. The angular momentum of each ball about point of contact is coserved.
For ball 1: MRV′1+Iω′1=MRV''1+Iω′1
0+I(VR)=MRV''1+I(V''1R)
V''1=VMR2I+1=27V
For ball 2: MRV′2+Iω′2=MRV''2+Iω''2
MRV=0=MRV''2(V''2R)
V''2=V1+IMR2=57V
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Single Correct
142 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.4
13 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
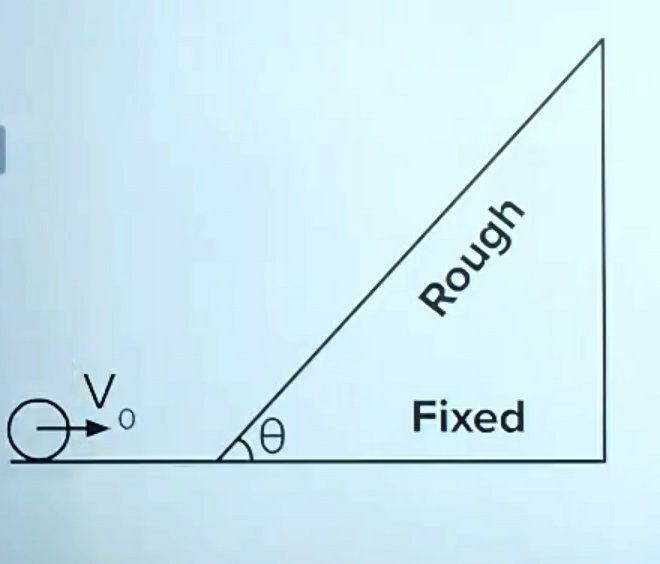
A solid spherical ball is rolling without slipping towards a fixed inclined plane with speed V0. Find the maximum height, that the ball reached on the incline.
View SolutionA heavy ball of mass 2M moving with a velocity v0 collides elastically head on with a cradle of three identical ball each of mass M as shown in figure. Determine the velocity of each ball after collision.
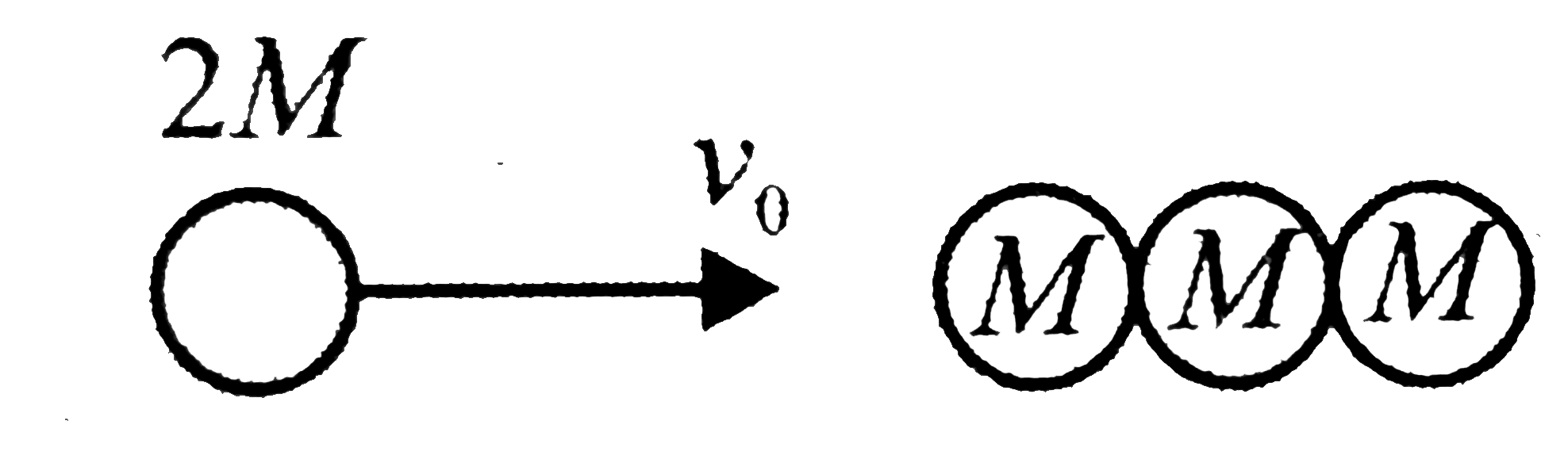
View Solution
Knowledge Check
A ball A of mass M collides elastically with a similar ball B at rest as shown in figure. Initially velocity of ball A is u m/s. After collision,
 ASpeed of ball B is u sinθBVelocity of ball A is usin2θˆi+usinθcosθˆjCSpeed of ball A is ucosθDVelocityofballBisu cos theta sin theta hati + u cos^2 theta hatj
ASpeed of ball B is u sinθBVelocity of ball A is usin2θˆi+usinθcosθˆjCSpeed of ball A is ucosθDVelocityofballBisu cos theta sin theta hati + u cos^2 theta hatjA solid spherical ball is rolling without slipping down an inclined plane. The fraction of its total kinetic energy associated with rotation is
A25B27C35D37A ball is rolling without slipping in a spherical shallow bowl (radius R) as shown in the figure and is executing simple harmonic motion. If the radius of the ball is doubled, the period of oscillation
 Aincreases slightlyBis reduced by a factor of 1/2Cis increased by a factor of 2Ddecreases slightly
Aincreases slightlyBis reduced by a factor of 1/2Cis increased by a factor of 2Ddecreases slightly
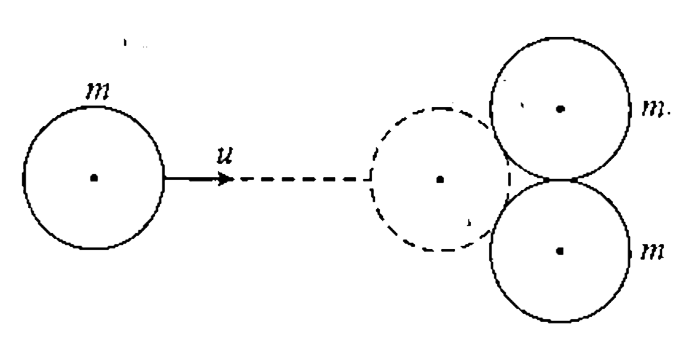
A ball with initial speed of10m/s collides elastically with two other identical balls at rest as shown in figure, whose centres are on a line perpendicular to the initial velocity and which are initially in contact with each other.All the three balls are lying on a smooth horizontal table. The first ball is aimed directly at the contact point of the other two balls.All the balls are smooth. Find the velocities of the three balls after the collision.
View SolutionA solid sphere is rolling without slipping on rough ground as shown in figure. It collides elastically with another identical sphere at rest. There is no friction between the two spheres. Radius of each sphere is R and mass is m.

Linear velocity of first sphere after it again starts rolling without slipping is:
View SolutionBall 1 collides with an another identical ball 2 at rest as shown in figure. For what value of coefficient of restitution e, the velocity of ball 2 becomes two times that of ball I after collision?
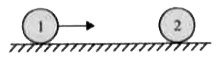
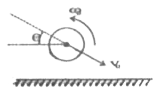
View SolutionA solid spherical ball of radius R collides with a rough horizontal surface as shown in figure. At the time of collision its velocity is v0 at an angle θ to the horizontal and angular velocity ω0 as shown . After collision, the angular velocity of ball may
View SolutionA solid sphere is rolling without slipping on rough ground as shown in figure. If collides elastically with an identical another sphere at rest. There is no friction between the two spheres . Radius of each sphere is R and mass is m.
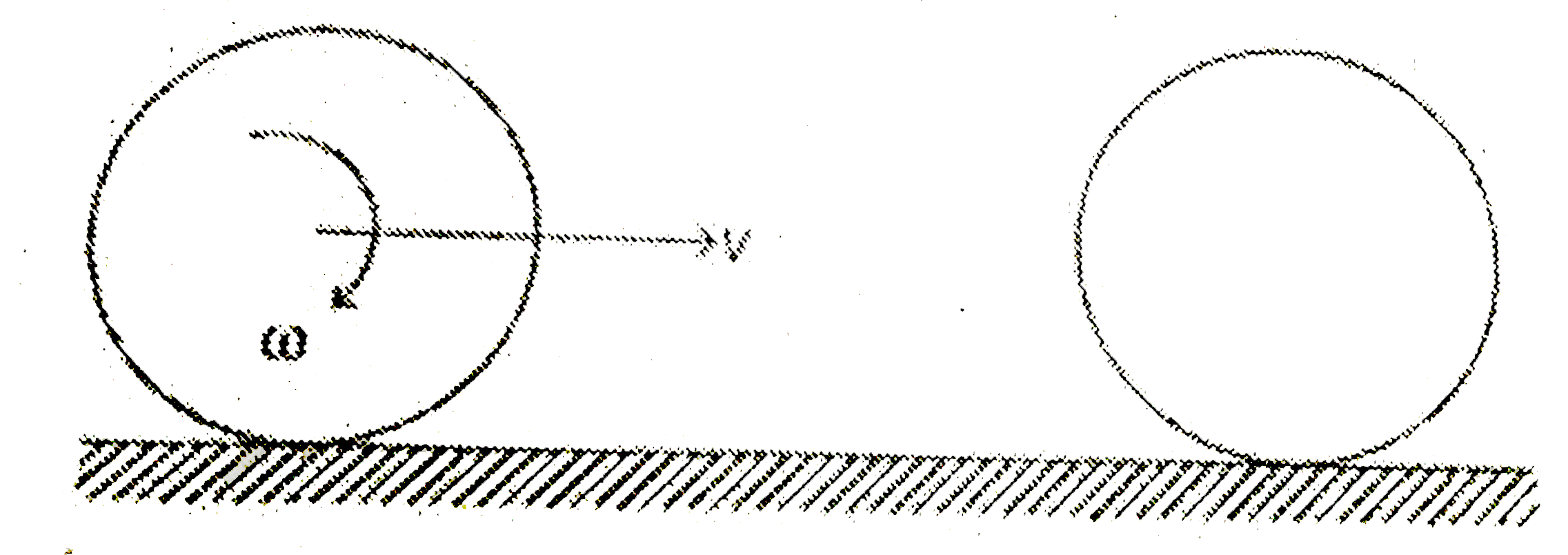
Linear velocity of first sphere after it again starts rolling without slipping is
View Solution
