A solid uniform cylinder of mass m performs small oscillations due to the action of two springs of stiffness k each (figure). Find the period of these oscillation in the absendce of sliding.
x
Let k1 and k2 be the spring constant of left and right sides springs. As the rolling of the solide cylinder is pure its lowest point becomes the instantaneous centre of rotation. If θ be the smaller angular displacement of its upper most point relavtive to its equilibrium position, the deformation of each spring becomes (2Rθ). Since the mechanical energy of oscillation of the solide cylinder is conserved, E=T+U= constant
i.e. 12Ip(.θ)2+12k1(2Rθ)2+12k2(2Rθ)2= constant
Differentiating w.r.t. time
12Ip2.θ..θ+12(k1+k2)4R22θ.θ=0
or, (mR22+mR2)..θ+4R2kθ=0
( Because Ip=IC+mR2=mR22+mR2)
Hence ..θ=−83kmθ
Thus ω0=8k3m and sourght time period
T=2πω0=2π√3m8k=π√3m2k
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electric Oscillations
56 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Elastic Waves
39 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
A solid unifom cylinder of mass M performs small oscillations due to the action of two speings, each having stiffness k. The period of these oscillations in absence of any sliding is 2π√xMyK. Find (x+y) (springs have their natural length initially).
'(##CEN_KSR_PHY_JEE_C16_E01_021_Q06##)'
View SolutionA small block oscillates back and forth on as smooth concave surface of radius R figure. Find the time period of small oscillation.

View Solution
Knowledge Check
A uniform cylinder of mass m and radius R is in equilibrium on an inclined plane by the action of a light spring of stiffness k, gravity and reaction force acting on it. If the angle of inclination of the plane is ϕ, then angular frequency of small oscillations of the cylinder is...........
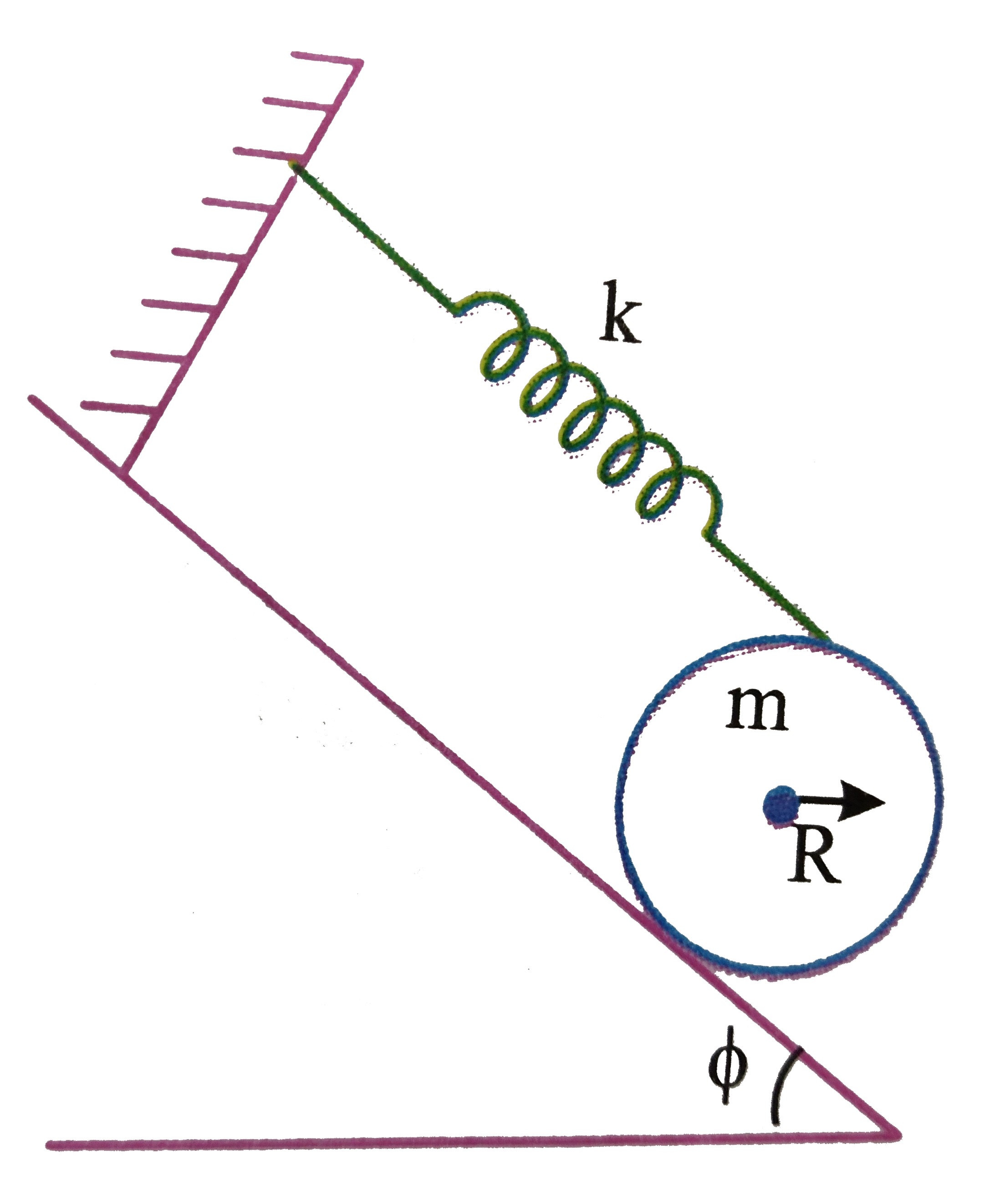 A2√kmB2√2kmC2√2k3mD√2km
A2√kmB2√2kmC2√2k3mD√2kmThe time period of small oscillations of mass m :-
_S01_040_Q01.png) A2π√m6kB2π√11m6KC2π√6m11KD2π√mK
A2π√m6kB2π√11m6KC2π√6m11KD2π√mKA particle of mass m is attached to three identical springs of spring constant k as shwon in figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mk
A solid uniform cylinder of mass M performs small oscillations in horizontal plane if slightly displaced from its mean position shown in figure. If it is given that initially springs are in natural lengths and cylinder does not slip on ground during oscillaitons due to frications between ground and cylinder. Force constant of each spring is k.
Find time period of these oscillation.
_S01_027_Q01.png)
View SolutionA uniform cylinder of mass m and radius R is in equilibrium on an inclined by the action of a light spring of stiffness, gravity and reaction force acting on it .If the angle of inclination of the plane is ϕ , find the angular frequency of small oscillation of the cylinder

View SolutionA solid cylinder of mass m length L and radius R is suspended by means of two ropes of length l each as shown. Find the time period of small angular oscillations of the cylinder about its axis AA'
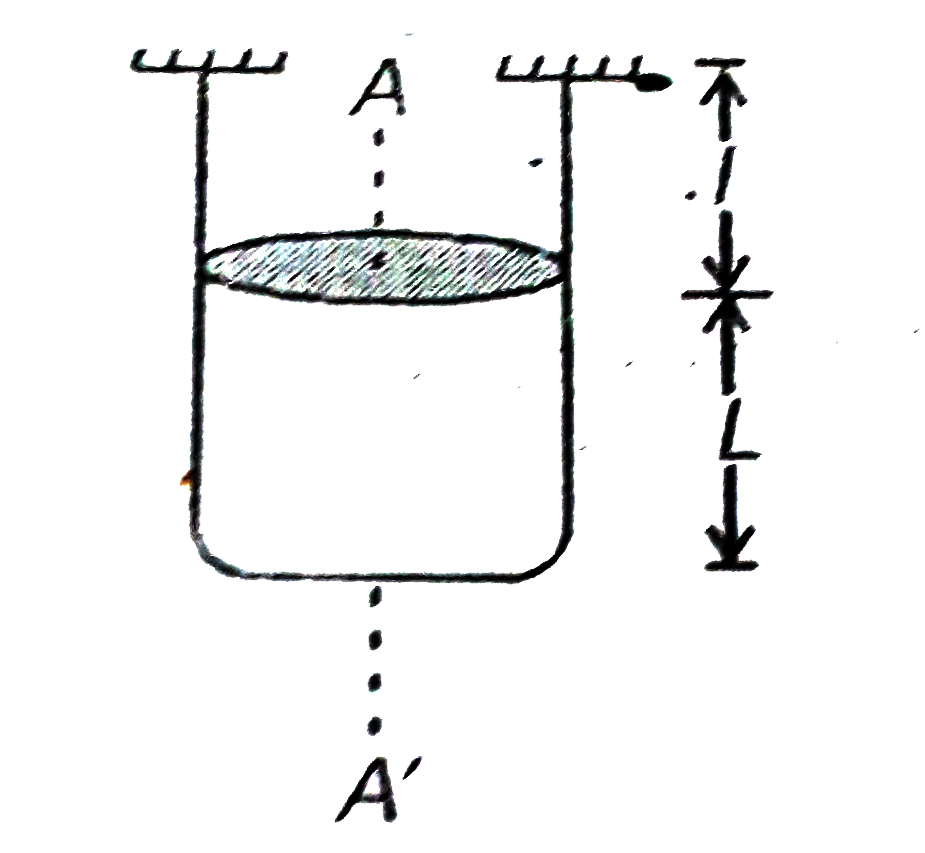
View Solution
The period of oscillation of a mass M suspended from a spring of spring constant K is T. the time period of oscillation of combined blocks is
View SolutionA uniform solid sphere of mass 'm' and radius R is in equilibrium on an inclined plane by the action of the light spring of stiffness k, gravity and on it. If the angle of inclination of the plane is 60∘, then find the time period of oscillation for small displancement.
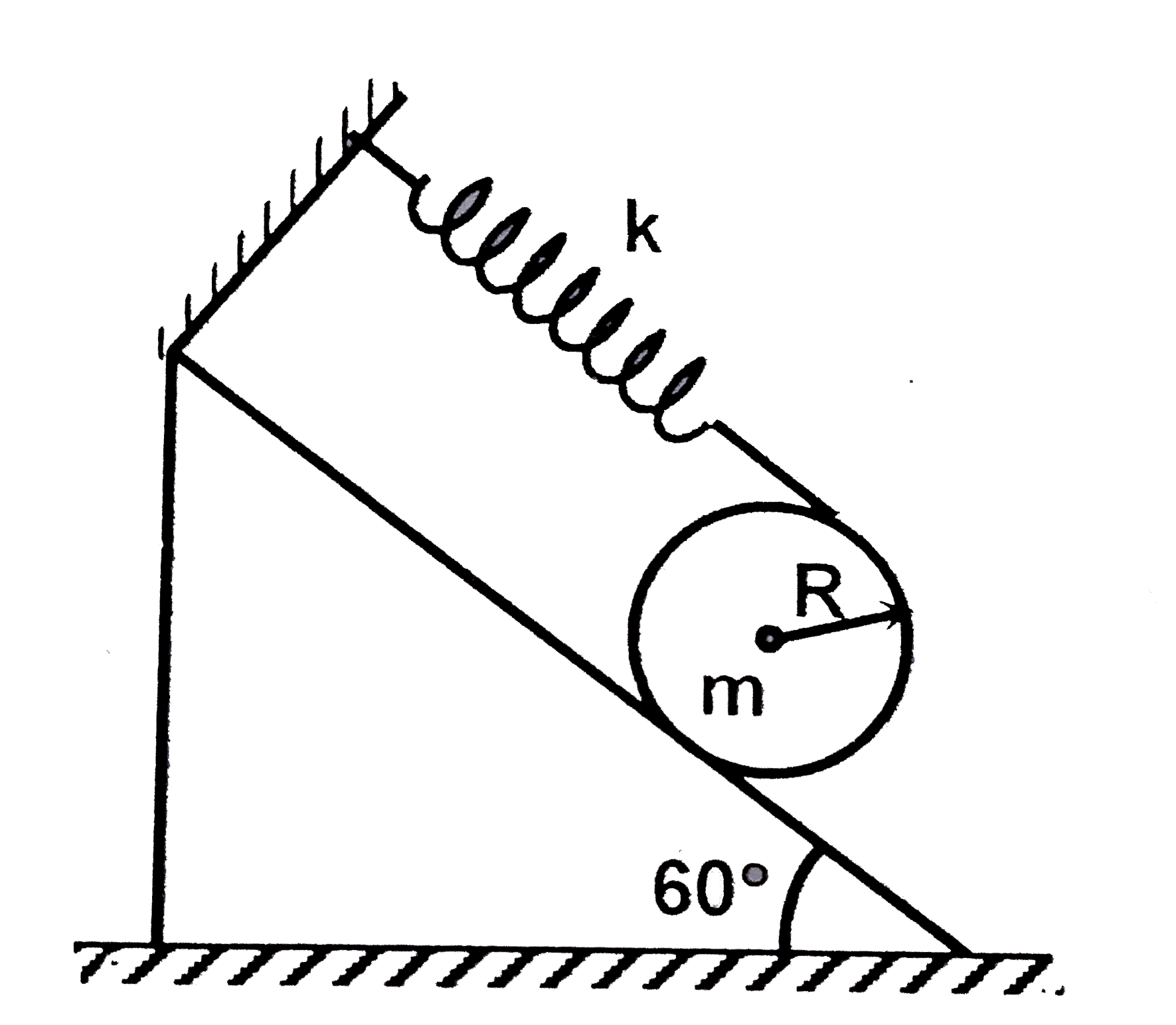
View Solution
