A solid uniform disc of mass m rols without slipping down a fixed inclined plank with an acceleration a. The frictional force on the disc due to surface of the plane is
14ma
32ma
ma
12ma
To find the frictional force on a solid uniform disc of mass m rolling without slipping down a fixed inclined plank with an acceleration a, we can follow these steps:
Step 1: Understand the motion of the disc
Since the disc rolls without slipping, there is a relationship between the linear acceleration a of the center of mass of the disc and its angular acceleration α. The relationship is given by:
\(
\alpha = \frac{a}{r}
\)
where r is the radius of the disc.
Step 2: Write the equation for torque
The only force that produces torque about the center of mass of the disc is the frictional force f. The torque τ due to the frictional force is given by:
\(
\tau = f \cdot r
\)
Step 3: Use the moment of inertia
The moment of inertia I of a solid uniform disc about its center is:
\(
I = \frac{1}{2} m r^2
\)
Step 4: Relate torque to angular acceleration
According to Newton's second law for rotation, the torque is also equal to the product of the moment of inertia and the angular acceleration:
\(
\tau = I \cdot \alpha
\)
Substituting the expressions for torque and moment of inertia, we have:
\(
f \cdot r = \left(\frac{1}{2} m r^2\right) \cdot \alpha
\)
Step 5: Substitute for angular acceleration
Now substitute α with ar:
\(
f \cdot r = \left(\frac{1}{2} m r^2\right) \cdot \left(\frac{a}{r}\right)
\)
Step 6: Simplify the equation
This simplifies to:
\(
f \cdot r = \frac{1}{2} m a r
\)
Dividing both sides by r (assuming r is not zero):
\(
f = \frac{1}{2} m a
\)
Final Answer
Thus, the frictional force on the disc due to the surface of the plane is:
\(
f = \frac{1}{2} m a
\)
---
Since the disc rolls without slipping, there is a relationship between the linear acceleration a of the center of mass of the disc and its angular acceleration α. The relationship is given by:
\(
\alpha = \frac{a}{r}
\)
where r is the radius of the disc.
The only force that produces torque about the center of mass of the disc is the frictional force f. The torque τ due to the frictional force is given by:
\(
\tau = f \cdot r
\)
The moment of inertia I of a solid uniform disc about its center is:
\(
I = \frac{1}{2} m r^2
\)
According to Newton's second law for rotation, the torque is also equal to the product of the moment of inertia and the angular acceleration:
\(
\tau = I \cdot \alpha
\)
Substituting the expressions for torque and moment of inertia, we have:
\(
f \cdot r = \left(\frac{1}{2} m r^2\right) \cdot \alpha
\)
Now substitute α with ar:
\(
f \cdot r = \left(\frac{1}{2} m r^2\right) \cdot \left(\frac{a}{r}\right)
\)
This simplifies to:
\(
f \cdot r = \frac{1}{2} m a r
\)
Dividing both sides by r (assuming r is not zero):
\(
f = \frac{1}{2} m a
\)
Thus, the frictional force on the disc due to the surface of the plane is:
\(
f = \frac{1}{2} m a
\)
Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Level 2
Explore 1 Video
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Level 2 Subjective
Explore 36 Videos
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Level 2 Single Correct
Explore 26 Videos
- ROTATIONBook:DC PANDEY ENGLISHChapter:ROTATIONExercise:(C) Chapter Exercises
Explore 39 Videos
- ROTATIONAL MOTIONBook:DC PANDEY ENGLISHChapter:ROTATIONAL MOTIONExercise:Integer Type Questions
Explore 17 Videos
Similar Questions
A solid uniform disc of mass m rolls without slipping down a fixed inclined plank with an acceleration a. The frictional force on the disc due to surface of the plane is
View SolutionA drum of radius R and mass M, rolls down without slipping along an inclined plane of angle θ. The frictional force-
View Solution
Knowledge Check
A cylinder of radius R and mass M rolls without slipping down a plane inclined at an angle θ. Coeff. of friction between the cylinder and the plane is μ. For what maximum inclination θ, the cylinder rolls without slipping ?
Atanθ gt 3μsBtanθ ≤ 3μsCtanθ lt 3μsDNone of theseA solid cylinder of mass M and radius R rolls without slipping down an inclined plane making an angle 6 with the horizontal. Then its acceleration is.
A1/3 g sinθB2/3 g sinθC2/5 g sinθD2/7 g sinθ
A solid sphere of mass m rolls without slipping on an inclined plane of inclination θ. The linear acceleration of the sphere is
View SolutionA disc and a solid sphere of same mass and radius roll down an inclined plane. The ratio of thhe friction force acting on the disc and sphere is
View Solution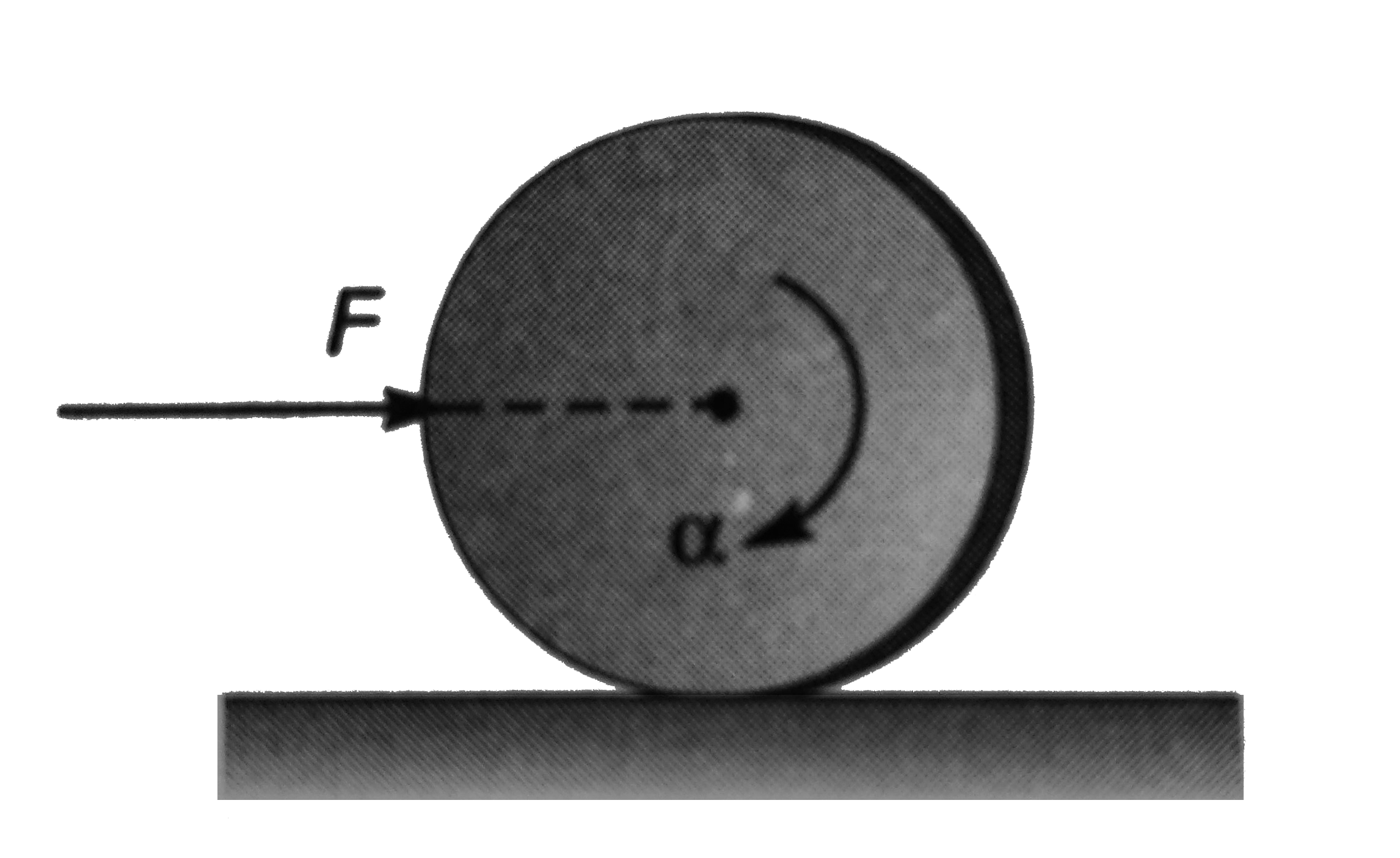
Consider a uniform disc of mass m, radius r rolling without slipping on a rough surface with linear acceleration a and angular acceleration α due to an external force F as shown in the figure coefficient of friction is μ.
Q. The magnitude of frictional force acting on the disc is
View Solution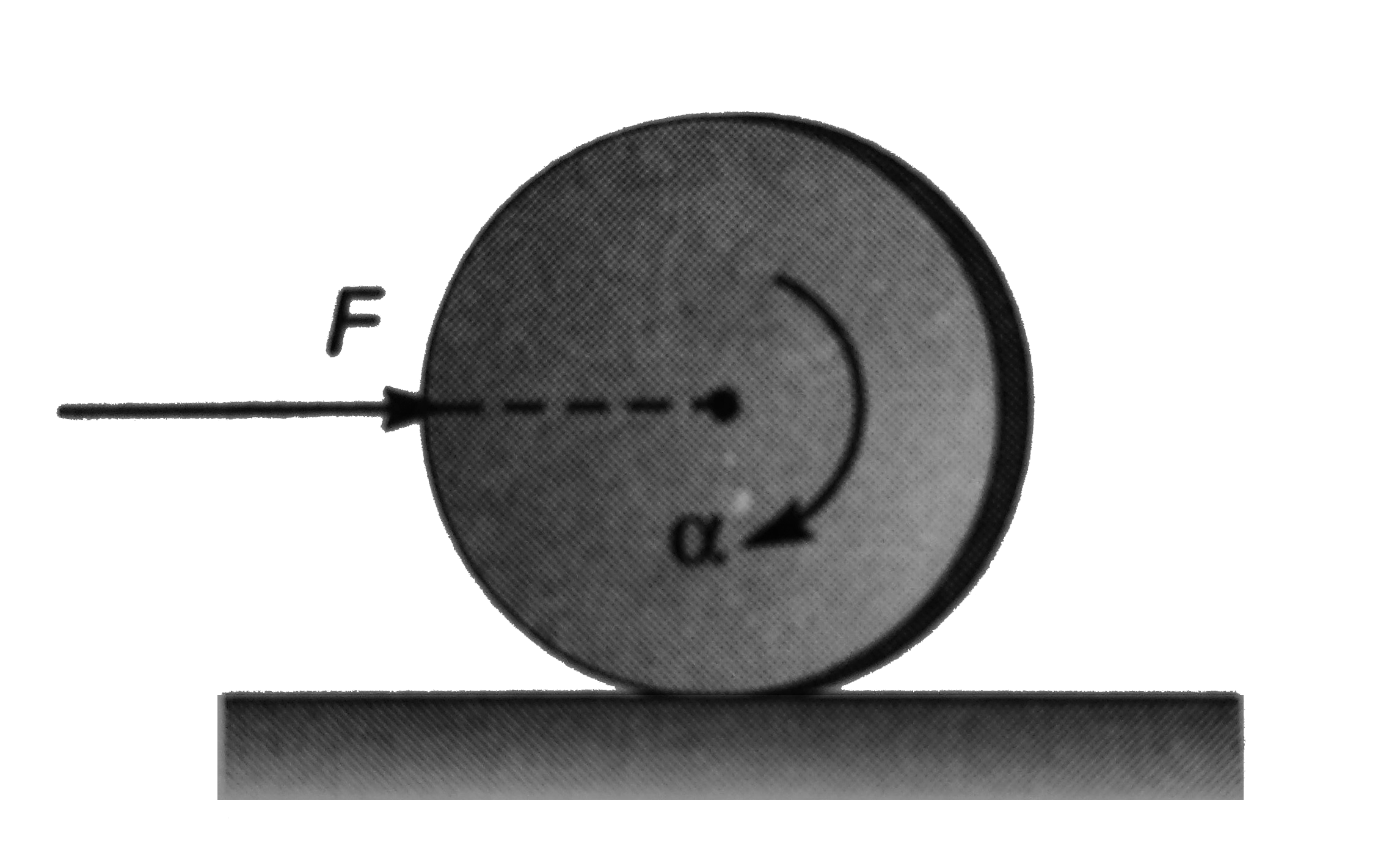
Consider a uniform disc of mass m, radius r rolling without slipping on a rough surface with linear acceleration a and angular acceleration α due to an external force F as shown in the figure coefficient of friction is μ.
Q. Angular momentum of the disc will be conserved about
View SolutionConsider a uniform disc of mass m, radius r rolling without slipping on a rough surface with linear acceleration a and angular acceleration α due to an external force F as shown in the figure coefficient of friction is μ.
Q. The work done by the frictional force at the instant of pure rolling is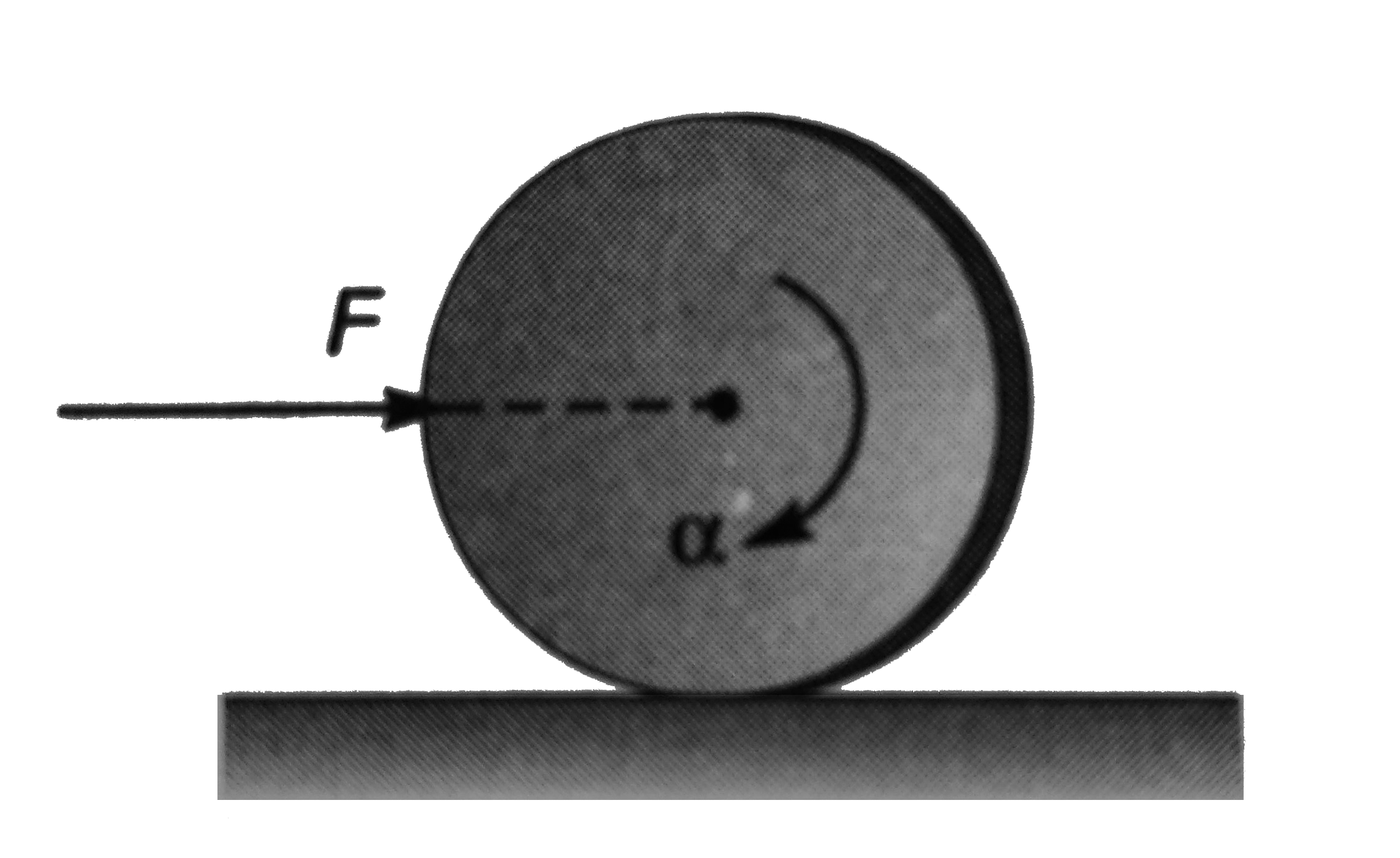
View SolutionA disc of mass 3 kg rolls down an inclined plane of height 5 m. The translational kinetic energy of the disc on reaching the bottom of the inclined plane is
View Solution