A uniform slender rod of mass m and length L is released from rest, with its lower end touching a frictionaless horizontal floor. At the initial moment, the rod is inclined at an angle θ=30∘ with the vertical. Thent he value of normal reaction from the from the floor just after release will be
4mg/7
5mg/9
2mg/5
None of these
To solve the problem of finding the normal reaction from the floor just after the release of a uniform slender rod inclined at an angle of θ=30∘ with the vertical, we can follow these steps:
Step 1: Draw the Diagram
We start by visualizing the problem. Draw a vertical line representing the vertical direction. Then, draw the rod inclined at 30∘ to the vertical. Label the lower end of the rod as point O (the point touching the floor) and the upper end as point P. The center of mass (C) of the rod is located at its midpoint.
Step 2: Identify Forces Acting on the Rod
The forces acting on the rod are:
- The weight of the rod mg acting downward through the center of mass.
- The normal reaction N acting upward at point O.
Step 3: Determine the Position of the Center of Mass
Since the rod is uniform, the center of mass is located at the midpoint of the rod. The distance from point O to the center of mass (C) can be calculated as:
OC=L2sin(30∘)=L2⋅12=L4
Step 4: Apply Newton's Second Law for Rotation
Using the rotational form of Newton's second law about point O, we have:
∑τ=Iα
where τ is the torque, I is the moment of inertia about point O, and α is the angular acceleration.
The torque due to the weight of the rod about point O is:
τ=mg⋅OC=mg⋅L4
Step 5: Calculate the Moment of Inertia
The moment of inertia I of a slender rod about one end is given by:
I=13mL2
Step 6: Relate Angular Acceleration to Linear Acceleration
The linear acceleration aC of the center of mass is related to the angular acceleration α by:
aC=OC⋅α
Substituting OC=L4:
aC=L4⋅α
Step 7: Apply Newton's Second Law for Translation
For the vertical motion, we can apply Newton's second law:
mg−N=maC
Substituting aC=L4⋅α:
mg−N=m(L4⋅α)
Step 8: Substitute for Angular Acceleration
From the torque equation:
mg⋅L4=Iα
Substituting for I:
mg⋅L4=13mL2α
Solving for α:
α=3gL
Step 9: Substitute Back to Find Normal Reaction
Now substituting α back into the equation for aC:
aC=L4⋅3gL=3g4
Now substituting aC back into the vertical motion equation:
mg−N=m(3g4)
This simplifies to:
N=mg−3mg4=14mg
Final Result
Thus, the normal reaction from the floor just after release is:
N=4mg7
We start by visualizing the problem. Draw a vertical line representing the vertical direction. Then, draw the rod inclined at 30∘ to the vertical. Label the lower end of the rod as point O (the point touching the floor) and the upper end as point P. The center of mass (C) of the rod is located at its midpoint.
The forces acting on the rod are:
- The weight of the rod mg acting downward through the center of mass.
- The normal reaction N acting upward at point O.
Since the rod is uniform, the center of mass is located at the midpoint of the rod. The distance from point O to the center of mass (C) can be calculated as:
OC=L2sin(30∘)=L2⋅12=L4
Using the rotational form of Newton's second law about point O, we have:
∑τ=Iα
where τ is the torque, I is the moment of inertia about point O, and α is the angular acceleration.
τ=mg⋅OC=mg⋅L4
The moment of inertia I of a slender rod about one end is given by:
I=13mL2
The linear acceleration aC of the center of mass is related to the angular acceleration α by:
aC=OC⋅α
Substituting OC=L4:
aC=L4⋅α
For the vertical motion, we can apply Newton's second law:
mg−N=maC
Substituting aC=L4⋅α:
mg−N=m(L4⋅α)
From the torque equation:
mg⋅L4=Iα
Substituting for I:
mg⋅L4=13mL2α
Solving for α:
α=3gL
Now substituting α back into the equation for aC:
aC=L4⋅3gL=3g4
Now substituting aC back into the vertical motion equation:
mg−N=m(3g4)
This simplifies to:
N=mg−3mg4=14mg
Thus, the normal reaction from the floor just after release is:
N=4mg7
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2
1 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Subjective
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Single Correct
26 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A uniform slender rod of mass m and length L is released from rest, with its lower end touching a frictionaless horizontal floor. At the initial moment, the rod is inclined at an angle θ=30∘ with the vertical. Thent he value of normal reaction from the from the floor just after release will be 4mg /7 In the above problem, the initial acceleration of the lower end of the rod will be
View SolutionA thin rod of mass M and length L is released from rest in position shown. The path of centre of mass of rod till the rod become horizontal is [ Assume surface is smooth]
_PHY_208_Q01.png)
View SolutionA uniform rod of mass m, hinged at its upper end, is released from rest from a horizontal position. When it passes through the vertical position, the force on the hinge is
View SolutionA rod of length 1 m is released from rest as shown in the figure below: If ω of rod is √n at the moment it hits the ground, then find n.
View SolutionA thin uniform rod mass M and length L is hinged at its upper end. And released from rest from a horizontal position. The tenstion at a point located at a distance L/3 from the hinge point, when the rod become vertical will
View SolutionA ladder of length L is slipping with its ends against a vertical wall and a horizontal floor. At a certain moment, the speed of the end in contact with the horizontal floor is v and the ladder makes an angle θ=30∘ with horizontal. Then, the speed of the ladder's centre of mass must be
View SolutionA rod of length l is pivoted about a horizontal , frictionless pin through one end. The rod is released from ret in a vertical position. Find the velocity of the CM of the rod when the rod is inclined at an angle θ from the vertical.

View SolutionThe end 'A' of a uniform rod AB of length 'l' touches a horizontal smooth fixed surface. Initially the rod makes an angle of 30∘ with the vertical. Find the magnitude of displacement of the end B just before it touches the ground after the rod is released.
View SolutionA uniform rod of mass m and length l is released from rest from its vertical position by giving a gently push. In consequence, the end of the rod collides at P after rotating about the smooth horizontal axis O. If the coefficient of restitution e=(12). Find the: a. angular speed of the rod just after the impact.
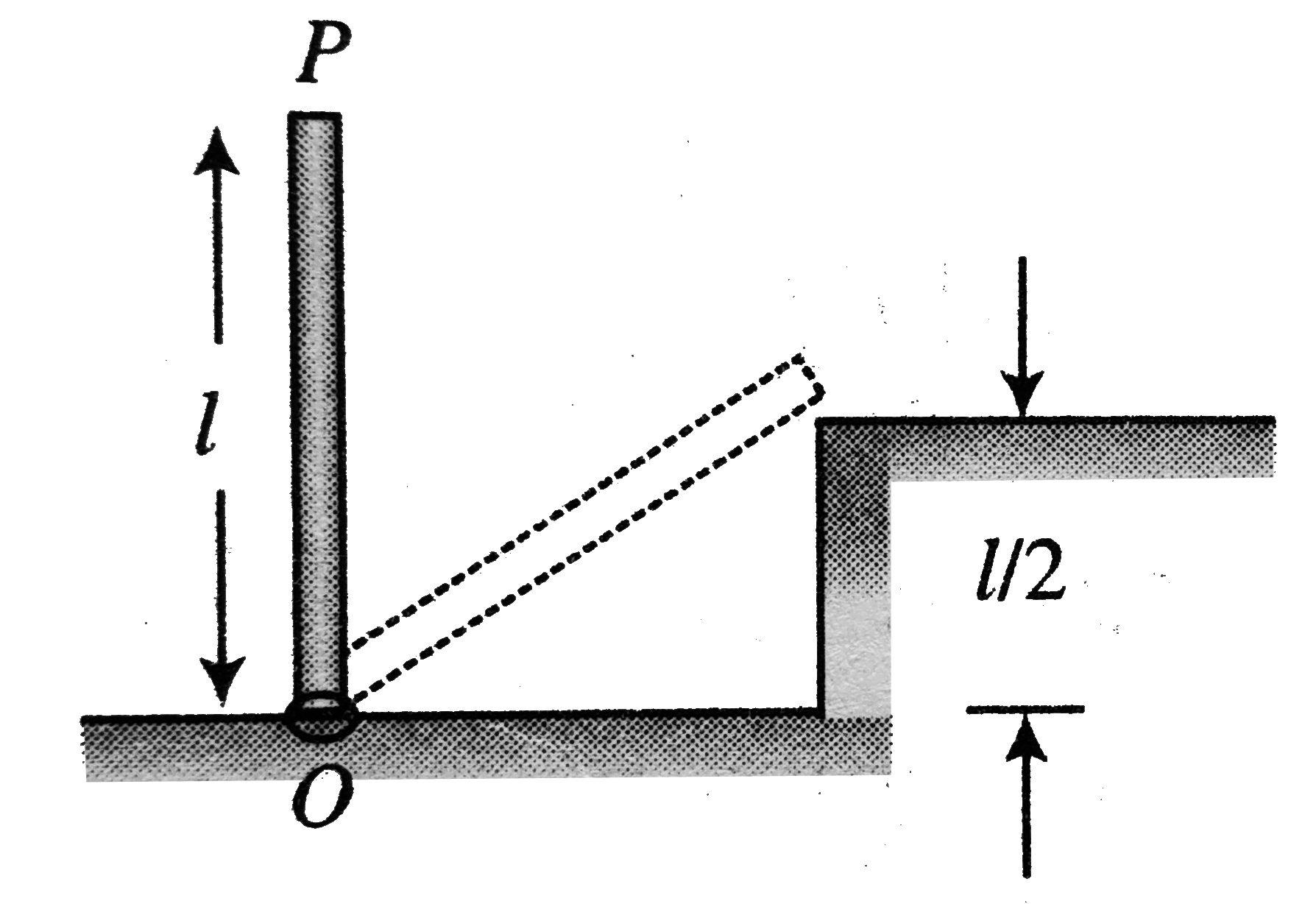
b. energy loss during collision. c. maximum angle rotated by rod after collision.
View SolutionA uniform slender bar B of mass m and length L supported by a firctionless pivot at A is released from rest at its vertical position as shown the figure. Calculate the reaction at pivot when the bar just acquires the horizontal position shown dotted.

View Solution
