A source contains two phosphorus radionuclides .15P35(T1/2=14.3days) and .15P33(T1/2=25.3days). Initially, 10% of the decays come from .15P35. How long one must wait until 90% do so?
To solve the problem, we need to find the time T required for the decays from the phosphorus radionuclide 15P35 to constitute 90% of the total decays, given that initially 10% of the decays come from 15P35 and 90% from 15P33.
1. Define Initial Conditions:
Let the initial number of nuclei of 15P35 be X and the initial number of nuclei of 15P33 be 9X (since 10% comes from 15P35 and 90% from 15P33).
2. Decay Formulas:
The number of nuclei remaining after time T can be expressed using the decay formula:
N(t)=N0(12)tT1/2
where N0 is the initial number of nuclei, t is the time, and T1/2 is the half-life.
3. Set Up Equations for Both Radionuclides:
For 15P35:
N35(T)=X(12)T14.3
For 15P33:
N33(T)=9X(12)T25.3
4. Determine the Condition for 90% Decay from 15P35:
We want N35(T) to be 90% of the total decays. Therefore, we set up the equation:
N35(T)=0.9⋅(N35(T)+N33(T))
This can be rearranged to:
N35(T)=0.9⋅(X(12)T14.3+9X(12)T25.3)
5. Simplifying the Equation:
Dividing through by X:
(12)T14.3=0.9⎛⎝(12)T14.3+9(12)T25.3⎞⎠
6. Rearranging and Solving:
Rearranging gives:
(12)T14.3−0.9(12)T14.3=8.1(12)T25.3
This simplifies to:
0.1(12)T14.3=8.1(12)T25.3
7. Taking Logarithms:
Taking logarithms on both sides:
log(0.1)+T14.3log(12)=log(8.1)+T25.3log(12)
8. Isolating T:
Rearranging gives:
T⎛⎜
⎜⎝log(12)14.3−log(12)25.3⎞⎟
⎟⎠=log(8.1)−log(0.1)
Solving for T:
T=log(8.1)−log(0.1)log(12)14.3−log(12)25.3
9. Calculating the Values:
Substitute the values of logarithms and calculate T.
Final Answer:
After performing the calculations, we find that T≈2808.5 days.
Let the initial number of nuclei of 15P35 be X and the initial number of nuclei of 15P33 be 9X (since 10% comes from 15P35 and 90% from 15P33).
The number of nuclei remaining after time T can be expressed using the decay formula:
N(t)=N0(12)tT1/2
where N0 is the initial number of nuclei, t is the time, and T1/2 is the half-life.
For 15P35:
N35(T)=X(12)T14.3
For 15P33:
N33(T)=9X(12)T25.3
We want N35(T) to be 90% of the total decays. Therefore, we set up the equation:
N35(T)=0.9⋅(N35(T)+N33(T))
This can be rearranged to:
N35(T)=0.9⋅(X(12)T14.3+9X(12)T25.3)
Dividing through by X:
(12)T14.3=0.9⎛⎝(12)T14.3+9(12)T25.3⎞⎠
Rearranging gives:
(12)T14.3−0.9(12)T14.3=8.1(12)T25.3
This simplifies to:
0.1(12)T14.3=8.1(12)T25.3
Taking logarithms on both sides:
log(0.1)+T14.3log(12)=log(8.1)+T25.3log(12)
Rearranging gives:
T⎛⎜
⎜⎝log(12)14.3−log(12)25.3⎞⎟
⎟⎠=log(8.1)−log(0.1)
Solving for T:
T=log(8.1)−log(0.1)log(12)14.3−log(12)25.3
Substitute the values of logarithms and calculate T.
After performing the calculations, we find that T≈2808.5 days.
Topper's Solved these Questions
- NUCLEIBOOK - NCERT ENGLISHCHAPTER - NUCLEIEXERCISE - Exercise
31 Videos
- MOVING CHARGES AND MANGNETISM BOOK - NCERT ENGLISHCHAPTER - MOVING CHARGES AND MANGNETISM EXERCISE - Exercise
28 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Exercise
32 Videos
Similar Questions
Phospheric acid (H3PO4) perpared in two step process .
(1) P4+5O2→P4O10 (2)P4O10+6H2O→4H3PO4
Well allow 62 g of phosphrous to react with exces oxygen which from P4O10 in 85% yield . In the sep (2) reaction 90% yield of H3PO4 is obtained . Mass of H3PO4 produced is :
View SolutionThe direction cosines of the line drawn from P(−5,3,1) to Q(1,5,-2) is
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
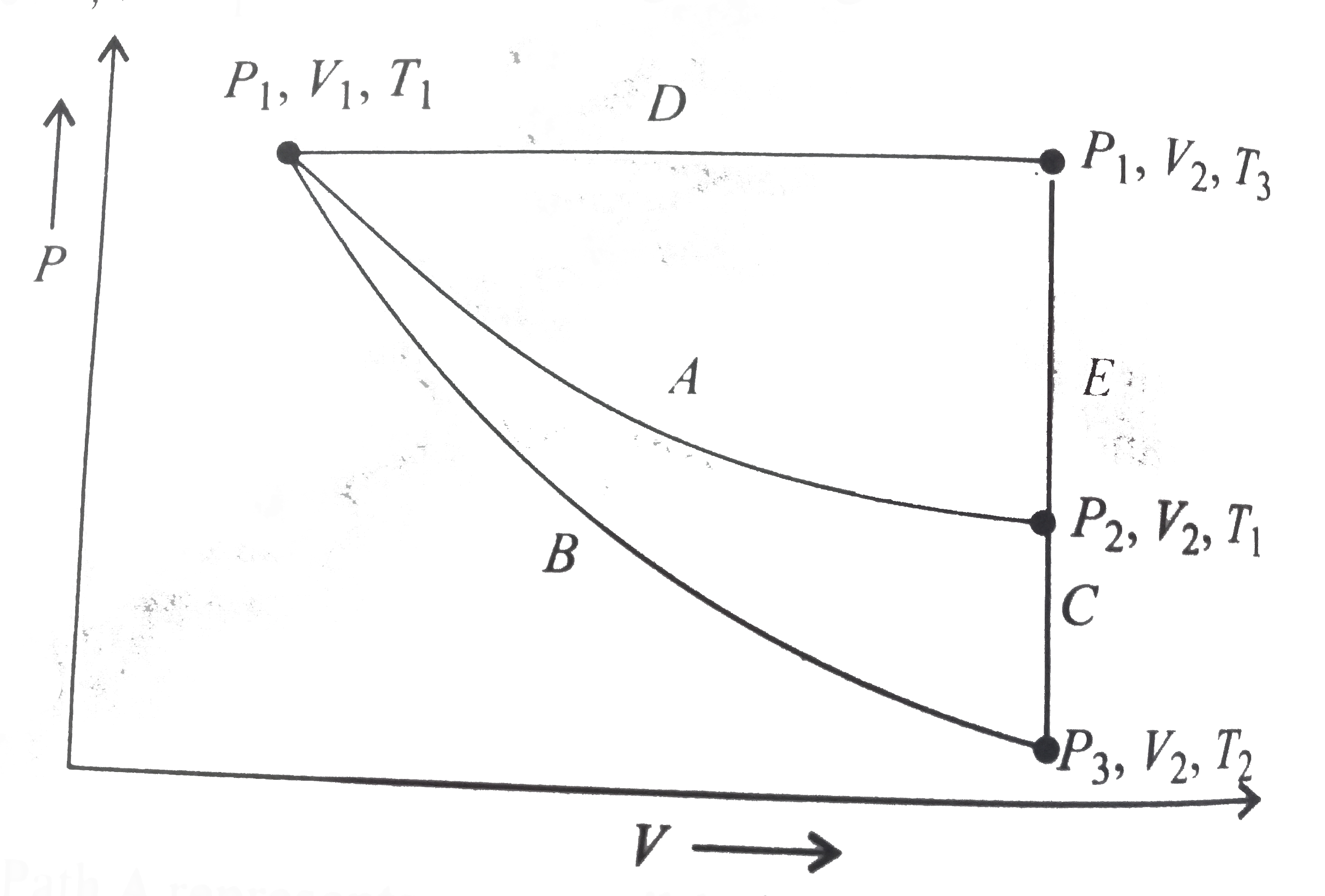
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is ΔS for path (D+E)?
View SolutionA computer producing factory has only two plants T1 and T2. Plant T1 produces 20% and plant T2 produces 80% of the total computers produced. 7% of computers produced in the factory turn out to be defective. It is known that P(computer turns out to bedefective, given that it is produced in plant T1)=10P (computer turns out to be defective, given that it is produced in plant T2), where P(E) denotes the probability of an event E.A computer produced in the factory is randomly selected and it does not turn out to be defective. Then, the probability that it is produced in plant T2, is
View SolutionConsider the following nuclear reaction
.21D+.21_D→.31D+.11P
Given that m(_(1)3T)=3.01605 amu,
m(_(1)3p)=1.00728 amu
The mass of deuterium (.21D) required per day in order to produce a power output of 109W (with 50% efficiency) is n.3 kg where n is a digit. Find n
View SolutionA fusion reaction of the type given below
.21D+.21D→.31T+.11p+ΔE
is most promising for the production of power. Here D and T stand for deuterium and tritium, respectively. Calculate the mass of deuterium required per day for a power output of 109W. Assume the efficiency of the process to be 50%.
Given : m(.21D)=2.01458amu, m(.31T)=3.01605amu
m(.11p)=1.00728amu and 1amu=930MeV.
View SolutionThe % yield of ammonia as a function of time in the reaction, N2(g)+3H2(g)⇔2NH3(g)'ΔH<0
at (p,T1) is given below
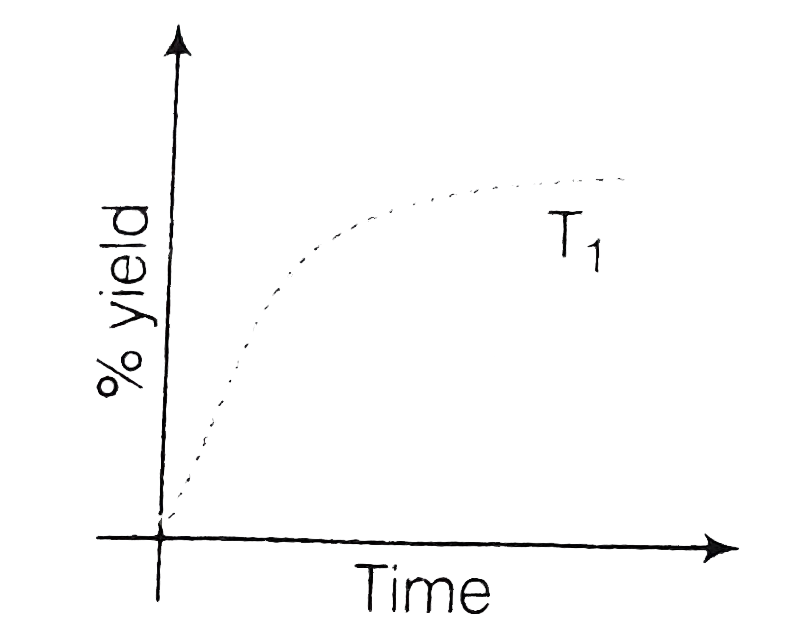
If this reaction is conducted at (p,T1), with T2>T1 the % yield by of ammonia as a function of time is represented by
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
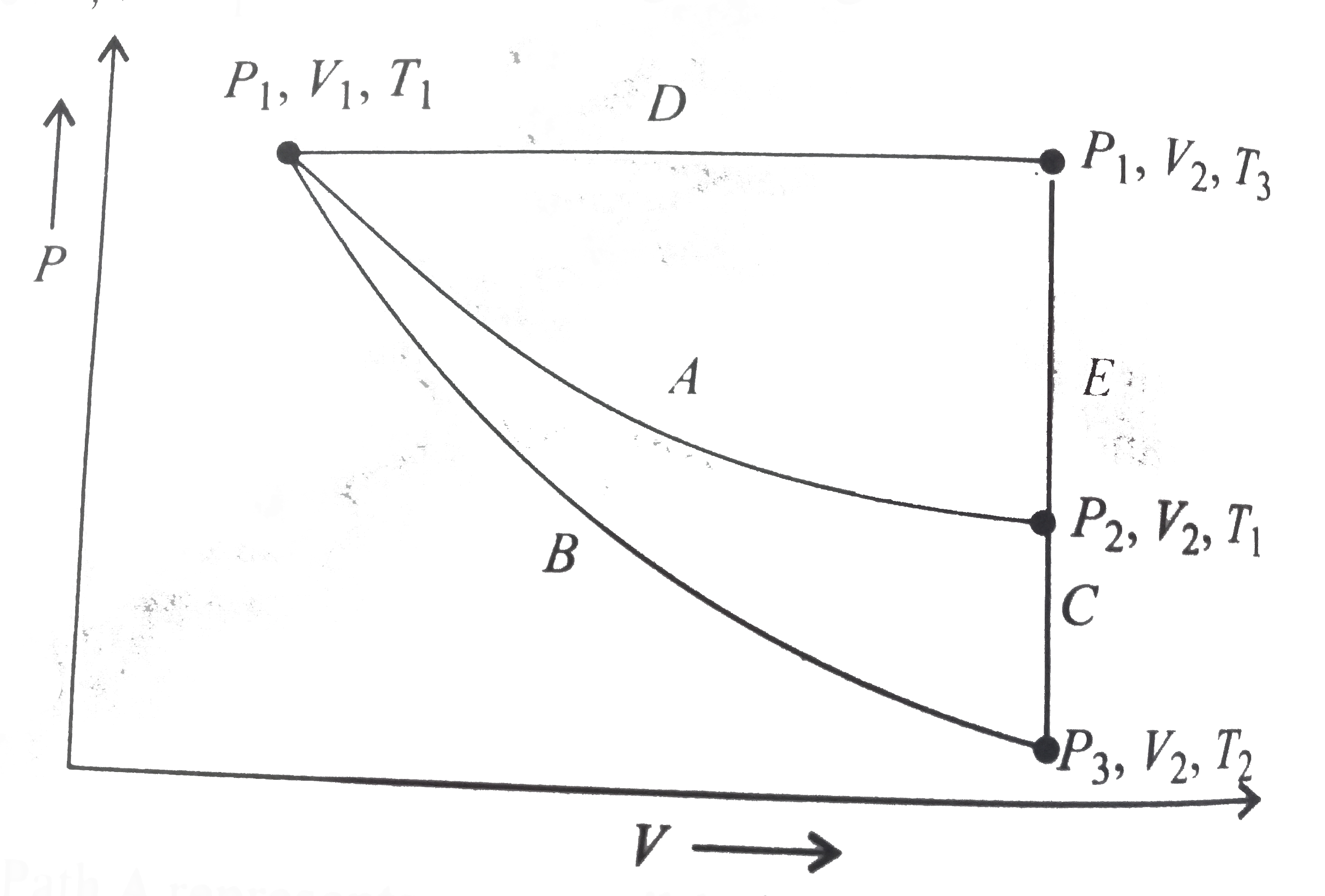
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is qrev, for path (D+E)?
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
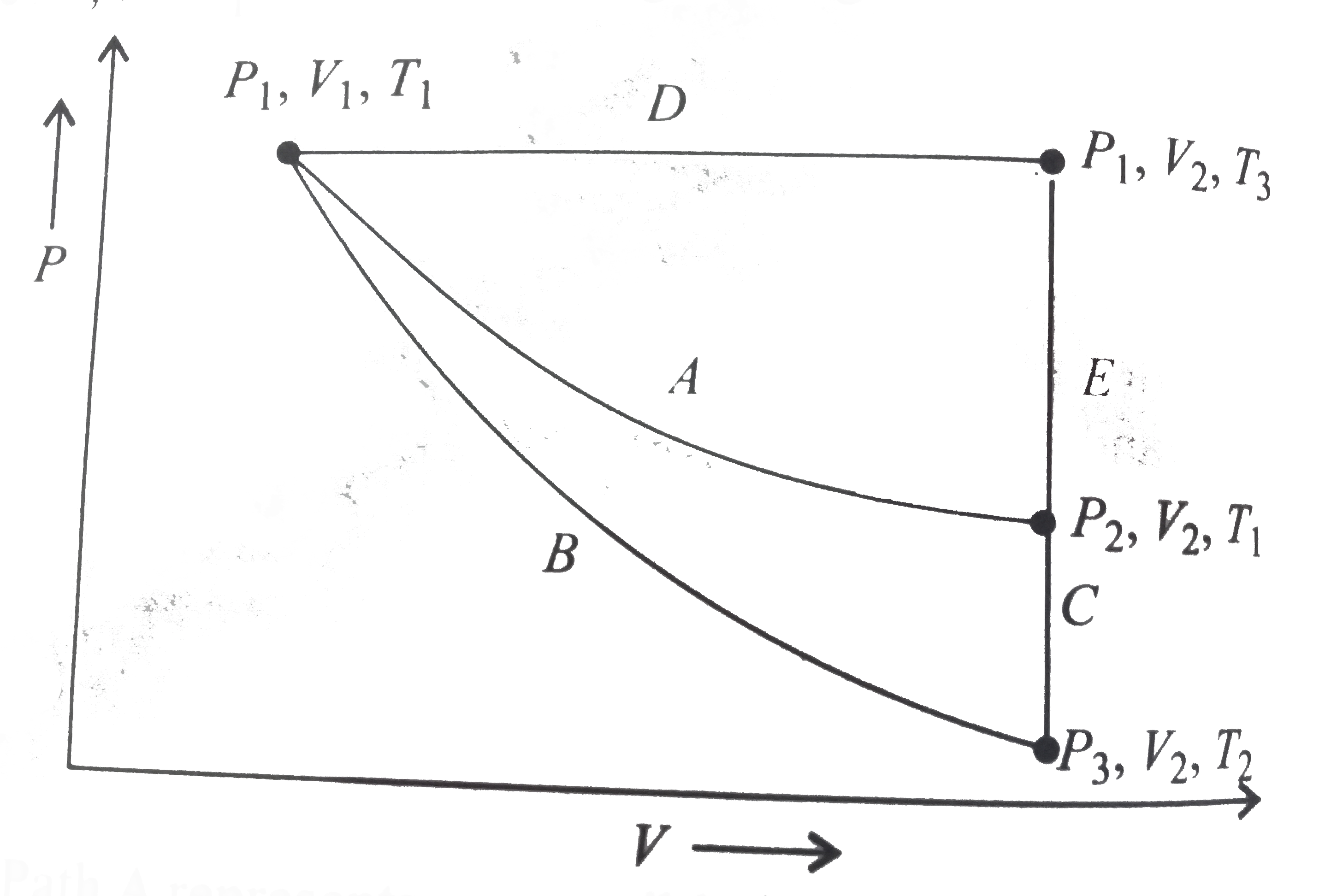
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is qrev, for path (A)?
View SolutionFor an ideal gas, an illustration of three different paths A,(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.

Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is qrev, for path A?
View Solution
