A sphere of mass m, impinges obliquely on a sphere, of mass M, which is at rest. Show that, if m=eM, the directions of motion of the sphere after impact are at right angles.
To solve the problem, we need to analyze the collision between two spheres, one of mass m and the other of mass M, where the mass m is moving and the mass M is at rest. We are given that m=eM, where e is the coefficient of restitution. We need to show that the directions of motion of the spheres after the impact are at right angles.
1. Understanding the Collision:
- Let the mass m be moving with an initial velocity →Vm towards the stationary mass M.
- The collision occurs along the line of impact. We can define the direction of the incoming mass m as the x-axis and the direction perpendicular to it as the y-axis.
2. Conservation of Linear Momentum:
- Since no external forces are acting on the system, we can apply the conservation of linear momentum along the line of collision.
- Before the collision, the momentum of the system is:
pinitial=m→Vm+M⋅0=m→Vm
- After the collision, let the velocities of masses m and M be →V′m and →V′M respectively. The momentum after the collision is:
pfinal=m→V′m+M→V′M
- By conservation of momentum:
m→Vm=m→V′m+M→V′M(1)
3. Coefficient of Restitution:
- The coefficient of restitution e is defined as:
e=Velocity of separationVelocity of approach
- For our case, the velocity of approach is Vm (the initial velocity of mass m), and the velocity of separation is V′M+V′m (the velocities of both masses after collision).
- Thus, we can write:
e=V′M+V′mVm(2)
4. Substituting m=eM:
- From the problem, we have m=eM. Substituting this into equation (1):
eM→Vm=eM→V′m+M→V′M
- Dividing through by M:
emM→Vm=e→V′m+→V′M
5. Analyzing the Directions:
- From the coefficient of restitution equation (2), we can set up the equations for the velocities after the collision.
- If we assume that →V′m and →V′M are at right angles, we can express their relationship in terms of trigonometric identities.
- If →V′m is in the x-direction and →V′M is in the y-direction, we can write:
V′M=eVmandV′m=0
- This leads to the conclusion that the two velocities are perpendicular.
6. Conclusion:
- Therefore, we have shown that if m=eM, the directions of motion of the two spheres after the impact are at right angles.
- Let the mass m be moving with an initial velocity →Vm towards the stationary mass M.
- The collision occurs along the line of impact. We can define the direction of the incoming mass m as the x-axis and the direction perpendicular to it as the y-axis.
- Since no external forces are acting on the system, we can apply the conservation of linear momentum along the line of collision.
- Before the collision, the momentum of the system is:
pinitial=m→Vm+M⋅0=m→Vm
- After the collision, let the velocities of masses m and M be →V′m and →V′M respectively. The momentum after the collision is:
pfinal=m→V′m+M→V′M
- By conservation of momentum:
m→Vm=m→V′m+M→V′M(1)
- The coefficient of restitution e is defined as:
e=Velocity of separationVelocity of approach
- For our case, the velocity of approach is Vm (the initial velocity of mass m), and the velocity of separation is V′M+V′m (the velocities of both masses after collision).
- Thus, we can write:
e=V′M+V′mVm(2)
- From the problem, we have m=eM. Substituting this into equation (1):
eM→Vm=eM→V′m+M→V′M
- Dividing through by M:
emM→Vm=e→V′m+→V′M
- From the coefficient of restitution equation (2), we can set up the equations for the velocities after the collision.
- If we assume that →V′m and →V′M are at right angles, we can express their relationship in terms of trigonometric identities.
- If →V′m is in the x-direction and →V′M is in the y-direction, we can write:
V′M=eVmandV′m=0
- This leads to the conclusion that the two velocities are perpendicular.
- Therefore, we have shown that if m=eM, the directions of motion of the two spheres after the impact are at right angles.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Comprehension Based Questions
3 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
A ball of mass 2m impinges directly on a ball of mass m, which is at rest. If the velocity with which the larger ball impringes be equal to the velocity of the smaller mass after impact then the coefficient of restitution :-
View SolutionA sphere P of mass m moving with velocity u collides head on with another sphere Q of mass m which is at rest . The ratio of final velocity of Q to initial velocity of P is
( e = coefficient of restitution )
View SolutionA sphere of mass 10 kg and radius 0.5 m rotates about a tangent. The moment of inertia of the sphere is
View SolutionA sphere of mass m moves with a velocity 2v and collides inelastically with another identical sphere of mass m. After collision the first mass moves with velocity v in a direction perpendicular to the initial direction of motion . Find the speed of the second sphere after collision .
View SolutionA sphere of mass m falls on a smooth hemisphere of mass M resting with its plane face on smooth horizontal table, so that at the moment of impact, line joining the centres makes an angle with the vertical. The velocity of sphere just before impact is u and e is the coefficient of restitution.
View SolutionA hollow sphere of mass M lies on a rough horizontal plane when a particle of mass m traveling with speed v collides and sticks with it. If line of motion of the particle is at height h above the center of sphere, find h if the body rolls without slipping after collision (m<<M).
View SolutionA sphere of mass m1 in motion hits directly another sphere of mass m2 at rest and sticks to it, the total kinetic energy after collision is 2/3 of their total K.E. before collision. Find the ratio of m1:m2.
View SolutionA sphere of mass m moving with velocity v collides head-on with another sphere of the same mass at rest. If the coefficient of resistitution e=1/2, then what is the ratio of final velocity of the second sphere to the intial velocity of the first sphere ?
View SolutionStatement I: If a sphere of mass mmoving with speed u undergoes a perfectly elastic head-on collision with another sphere of heavier mass M at rest (M>m), then direction of velocity of sphere of mass m is reversed due to collision (no external force acts on system of two spheres).
Statement II: During a collision of spheres of unequal masses, the heavier mass exerts more force on the lighter mass in comparison to the force which lighter mass exerts on the heavier one,
View SolutionThe sphere shown in figure lies on a rough plane when a particle of mass m travelling at a speed v0 collides and sticks with it. If the line of motion of the particle is at a distance h above the plane, find a. the linear speed o the combined system just after the collision b. the angular speed of the system about the centre of the sphere just the collision c. the value of h for which the sphere starts pure rolling on the plane Assume that the mass M of the sphere is large compared to the mass of the particle so that the centre of mass of the combined system is not appreciably shifted from the centre of the sphere.
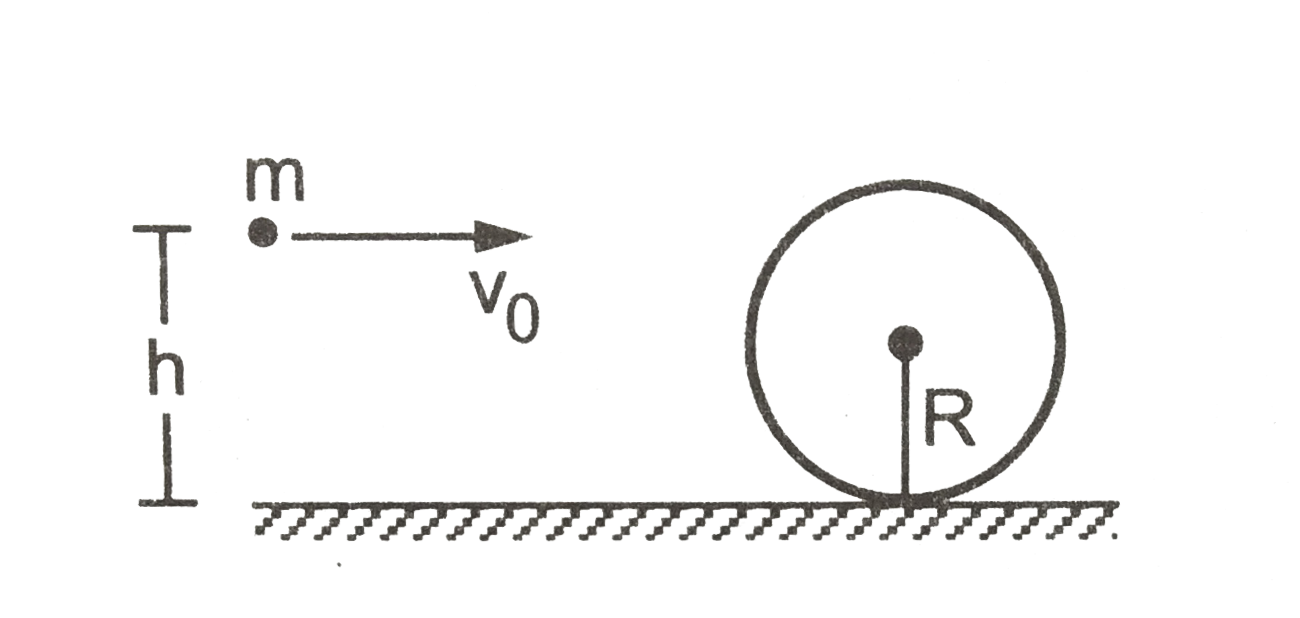
View Solution
