A spherical cavity is made inside a sphere of density, d. Its centre lies at a distance l, from the centre of sphere, show that the gravitational strength, I, of the field inside the cavity is =(4/3)×πGld.
Let centre C of the cavity be lying on the surface of a solid sphere of radius OC=l and density of earth =d. Fig.
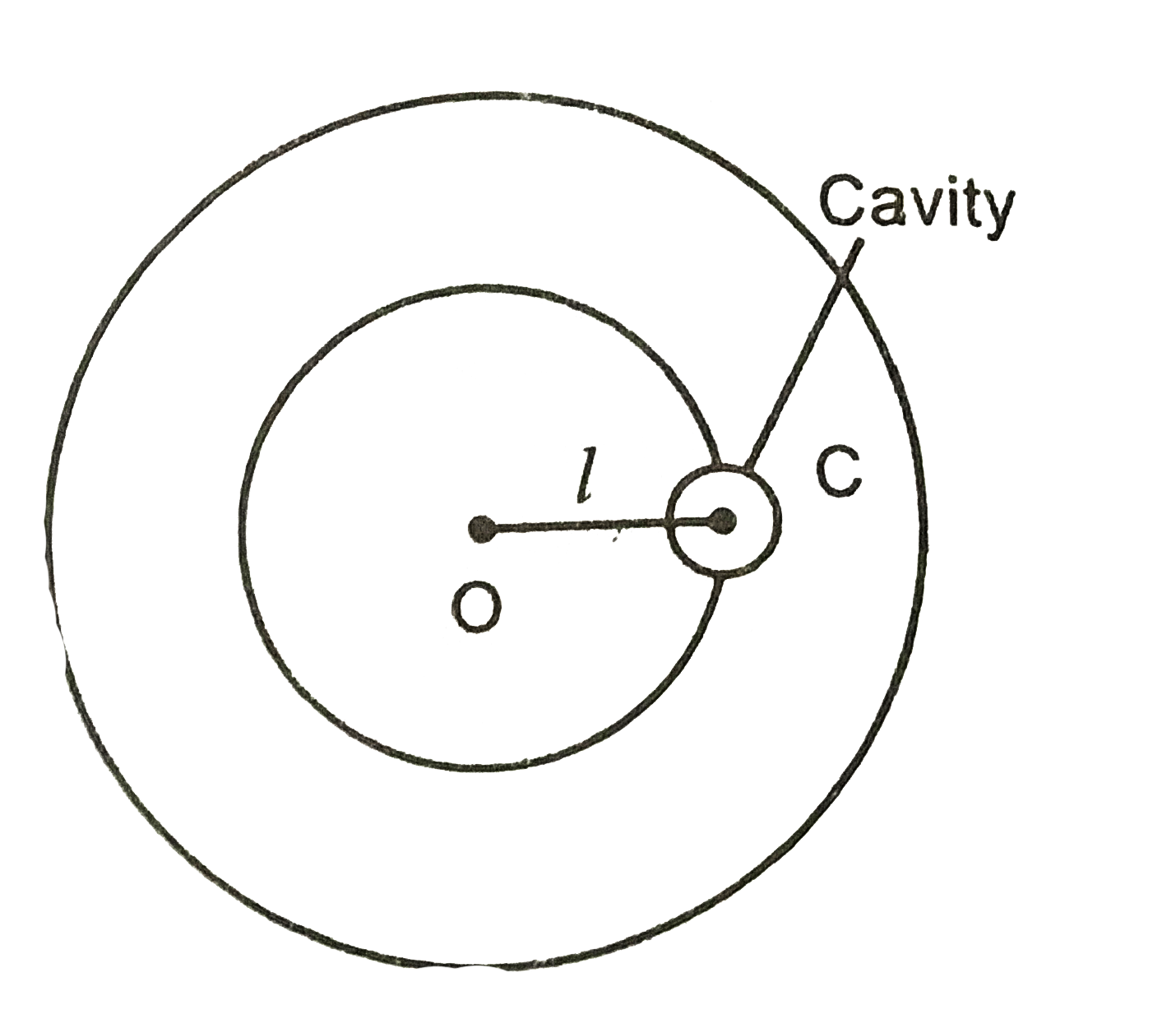
Mass of the shaded sphere, M=43πl3d
Gravitational intensity inside the cavity (i.e., at point C) is
I=GMl2=Gl2×43πl3d=43πGld
Topper's Solved these Questions
- GRAVIATIONBook:PRADEEPChapter:GRAVIATIONExercise:CONCEPTUAL PROBLEMS II.
Explore 1 Video
- GRAVIATIONBook:PRADEEPChapter:GRAVIATIONExercise:CONCEPTUAL PROBLEMS III.
Explore 1 Video
- GRAVIATIONBook:PRADEEPChapter:GRAVIATIONExercise:CONCEPTUAL PROBLEMS I.
Explore 1 Video
- BEHAVIOUR OF PERFECT GAS & KINETIC THEORYBook:PRADEEPChapter:BEHAVIOUR OF PERFECT GAS & KINETIC THEORYExercise:Assertion - Reason Type questions
Explore 14 Videos
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:1 NCERT Comprehension
Explore 4 Videos
Similar Questions
A spherical cavity is made inside a sphere of density ρ. If its centre lies at a distacne l from the centre of the sphere, show that the gravitational field strength of the field inside the cavatiy is
E=4π3Glρ
View SolutionInside a uniform sphere of density ρ there is a spherical cavity whose centre is at a distance l from the centre of the sphere. Find the strength G of the gravitational field inside the cavity.
View Solution
Knowledge Check
Inside a uniform sphere of density ρ there is a spherical cavity whose centre is at a distance l from the centre of the sphere. Find the strength of the gravitational field inside the cavity.
AE=−23πGρlBE=−43πGρlCE=−43π2GρlDE=−43πGρ2l2The figure represents a solid uniform sphere of mass M and radius R. A spherical cavity of radius r is at a distance a from the centre of the sphere. The gravitational field inside the cavity is
 Anon - uniformBtowards the center of the cavityCdirectly proportional to aDAll of these
Anon - uniformBtowards the center of the cavityCdirectly proportional to aDAll of theseA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of mass m at a distance R/2 from the centre of the sphere on the line joining both the centre of the cavity)
[Here g=(GM)/R2, where M is the mass of the sphereAmg2B3mg8Cmg16Dnone of these
A spherical cavity of radius R2 is made in a sphere of radius R and mass M. The centre of the cavity is at a distance R2 from the centre of the sphere. The intensity of gravitational field at the centre of cavity is GMnR2. Find n.
View SolutionA uniform solid of valume mass density ρ and radius R is shown in figure.
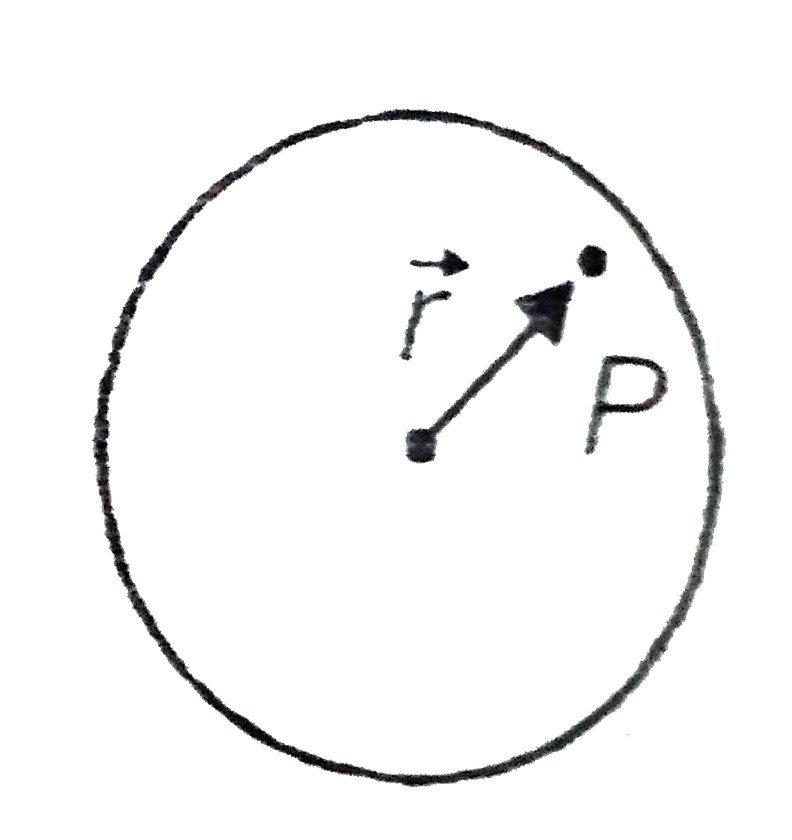
(a) Find the gravitational field at a point P inside the sphere at a distance r from the centre of the sphere. Represent the gravitational field vector →l in terms of radius vector →r of point P.
(b) Now a spherical cavity is made inside the solid sphere in such a way that the point P comes inside the cavity. The centre is at a distance a from the centre of solid sphere and point P is a distance of b from the centre of the cavity. Find the gravitational field →E at point P in vector formulationand interpret the result.
View SolutionA spherical cavity of radius r is made in a conducting sphere of radius 2 r.A charge q is kept at the centre of cavity as shown in the figure.Find the magnitude of the total electric field at (4r 0) .
View SolutionA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM/R2, where M is the mass of the solid sphere]
View SolutionA particle moving on the inside of a smooth sphere of radius r describing a horizontal circle at a distance r/2 below the centre of the sphere. What is its speed ?
View Solution