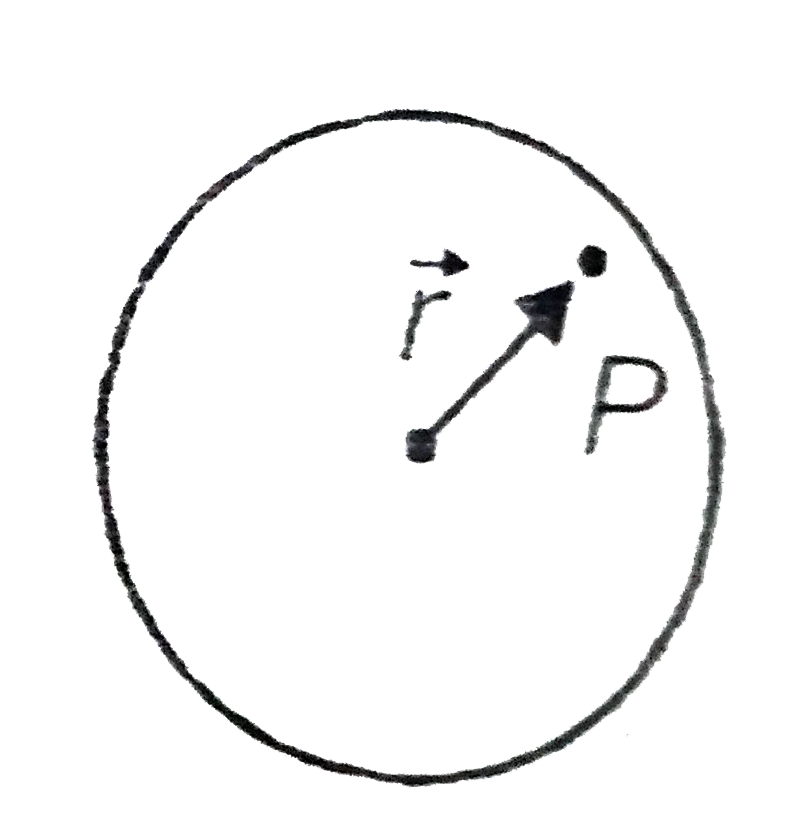
Inside a uniform sphere of density ρ there is a spherical cavity whose centre is at a distance l from the centre of the sphere. Find the strength G of the gravitational field inside the cavity.
Treating the cavity as negative mass of density −ρ in a uniform sphere density +ρ and using the superposition principle, the sought field strength is:
→G=→G1+→G2
or →G=−43πλρ→r++−43λπ(−ρ)→r−
(where →r+ and →r− are the position vectors of an orbitrary point P inside the cavity with respect to centre of sphere and cavity respectively.)
Thus →G=−43πγρ(→r+−→r−)=−43πγρ→l

Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Dynamics Of A Solid Body56videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Elastic Deformation Of Asolid Body25videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Laws Of Conservation Of Energy, Momentum And Angular Momentum82videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation36videos
OSCILLATIONS AND WAVES
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena38videos
THERMODYNAMICS AND MOLECULAR PHYSICS
Similar Questions
A spherical cavity is made inside a sphere of density ρ. If its centre lies at a distacne l from the centre of the sphere, show that the gravitational field strength of the field inside the cavatiy is
E=4π3GlρView SolutionA spherical cavity is made inside a sphere of density, d. Its centre lies at a distance l, from the centre of sphere, show that the gravitational strength, I, of the field inside the cavity is =(4/3)×πGld.
View Solution
Knowledge Check
- Question 1 - Select One
Inside a uniform sphere of density ρ there is a spherical cavity whose centre is at a distance l from the centre of the sphere. Find the strength of the gravitational field inside the cavity.
AE=−23πGρlBE=−43πGρlCE=−43π2GρlDE=−43πGρ2l2 - Question 2 - Select One
The figure represents a solid uniform sphere of mass M and radius R. A spherical cavity of radius r is at a distance a from the centre of the sphere. The gravitational field inside the cavity is
 Anon - uniformBtowards the center of the cavityCdirectly proportional to aDAll of these
Anon - uniformBtowards the center of the cavityCdirectly proportional to aDAll of these - Question 3 - Select One
A solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass m is
A11GMmR2B14GMmR2CGMm2R2DGMmR2
A spherical cavity of radius R2 is made in a sphere of radius R and mass M. The centre of the cavity is at a distance R2 from the centre of the sphere. The intensity of gravitational field at the centre of cavity is GMnR2. Find n.
View SolutionA uniform rig of mas m and radius a is placed directly above a uniform sphre of mass M and of equyal radius. The centre of the ring is at a distance √3 a from the centre of the sphere. Find the gravitational foerce exerted by the sphere on the ring.
View SolutionInside a ball charged uniformly with volume density ρ there is a spherical cavity. The centre of the ball by a distance a. Find the field strength E inside the cavity, assuming the permittively equal to unity.
View SolutionA sphere of radius R has a uniform volume density ρ. A spherical cavity of radius b, whose center lies at →a, is removed from the sphere.
i. Find the electric field at any point inside the spherical cavity.
ii. Find the electric field outside the cavity
(a) at points inside the large sphere but outside the cavity and
(b) at points outside the large sphere.
 View Solution
View SolutionA uniform solid of valume mass density ρ and radius R is shown in figure.
(a) Find the gravitational field at a point P inside the sphere at a distance r from the centre of the sphere. Represent the gravitational field vector →l in terms of radius vector →r of point P.
(b) Now a spherical cavity is made inside the solid sphere in such a way that the point P comes inside the cavity. The centre is at a distance a from the centre of solid sphere and point P is a distance of b from the centre of the cavity. Find the gravitational field →E at point P in vector formulationand interpret the result.View Solution

