A spherical volume contains a uniformaly distributed charge of density 2.0×104Cm3. Find the electric field at a piont inside the volume at a distance 4.0 cm from the centre.
Given: V = volume charge density
=2.0×(10−4)cm3
Inorder→f∈dthee≤ctricfieldatap∮
4cm=4×(10−2)momthecentre.
Let us assume a concentric spherical
surface inside the sphere.
Now, E×ds=(qε0)
But q=r×43π(r3)
So, E=(qε0.ds)
= (2 xx (10^-4) xx 4 pi (r^3) / (epsilon_0). 3 . 4 pi(r^2))<br>=2×(10−4)×r3ε0
=21.127×(105)NC
=3.0×(105)NC.
Topper's Solved these Questions
Similar Questions
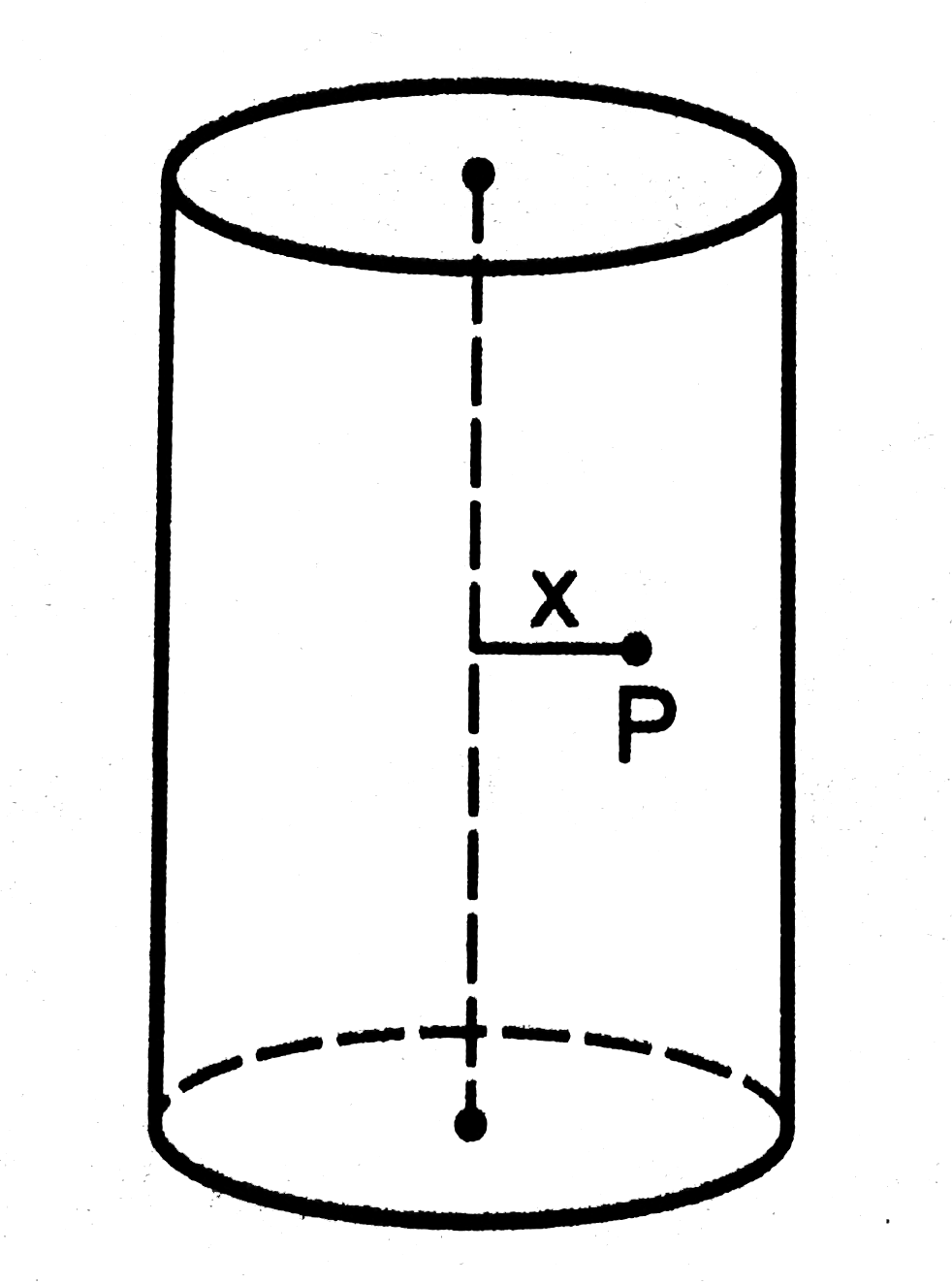
A long cylindrical volume contains a uniformly distributed charge of dendity ρ. Find the electric field at a point P inside the cylindrical volume at a distance x from its axis (figure 30-E5) ,
View SolutionA nonconducting sheet of large surface area and thickness d contains uniform charge distribution of density ρ. Find the electric field at a point P inside the plate, at a distance x from the central plane. Draw a qualitative graph of E against x for 0<x<<d.
View Solution
Knowledge Check
A long cylindrical volume (of radius R) contains a uniformly distributed charge of density ρ. Consider a point P inside the cylindrical volume at a distance x from its axis as shown in the figure. Here x can be more than or less than R. Electric field at point P is :
 Aρx2ε0 if x<RBρxε0 if x<RCρR24ε0x if x>RDρR22ε0x if x>R
Aρx2ε0 if x<RBρxε0 if x<RCρR24ε0x if x>RDρR22ε0x if x>RA ring of radius a contains a charge q distributed uniformly over its length. Find the electric field at a point on the axis of the ring at a distance x from the centre.
Akq2x(a2+x2)32B2kq2x(a2+x2)32Ckq2x(a2+x2)32Dkq22x(a2+x2)32The charges given to a hollow sphere of radius 10 cm is 10 n C . Electric field at a point situated at a distance of 4 cm from its centre is
A2250NC−1B56250NC−1C9000NC−1Dzero
A large conducting plane has a surface charge density 1.0×10−4cm−2.F∈dthee≤ctrostatice≠rgys→red∈acubicalvolumeofed≥1.0cm in front of the plane .
View SolutionA solid sphere of radius R has total charge Q. The charge is distributed in spherically symmetric manner in the sphere. The charge density is zero at the centre and increases linearly with distance from the centre. (a) Find the charge density at distance r from the centre of the sphere. (b) Find the magnitude of electric field at a point ‘P’ inside the sphere at distance r1 from the centre.
View SolutionA long wire carries a current of 4.00 A. Find the energy stored in the magnetic field inside a volume of 1.mm3 at a distance of 10.0 cm from the wire.
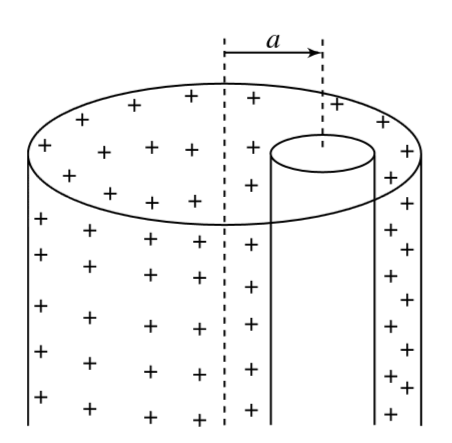
View Solution(a) There is a long uniformly charged cylinder having a volume charge density of ρC/m3. Radius of the cylinder is R. Find the electric field at a point at a distance x from the axis of the cylinder for following cases (i) x lt R (ii) x gt R What is the maximum field produced by the charge distribution at any point? (b) The cylinder described in (a) has a long cylindrical cavity. The axis of cylindrical cavity is at a distance a from the axis of the charged cylinder (see figure). Find electric field inside the cavity.
View SolutionAn infinitely long uniform linear charge distribution has a charge density 4 μC/m. what is the electric field at a point at a perpendicular distance of 3.6 cm from the line? Given: 14πε0=9×109Nm2/C2
View Solution
