A spool (consider it as a double disc system joined by a short tube at their centre) is placed on a horizontal surface as shown Fig. A light string wound several times over the short connecting tube leaves it tangentially and passes over a light pulley. A weight of mass m is attached to the end of the string. The radius of the connecting tube is r and mass of the spool is M and radius is R. Find the acceleration of the falling mass m. Neglect the mass of the connecting tube and slipping of the spool.

Since there is no slipping, the velocity of the point of contact of the string with the pulley is the vector sum of the velocity of the point of contact due to rotation plus the velocity of the centre of mass of the spool. That is
vB=vCM=ωr,ω is in clockwise direction.
But vCM=ωR
vB=vCM−vCMrR=vCM(R−rR)
This also the velocity v of the rolling mass
vB=vCM(R−rR)=v(R−rR)
Cosidering the conservation of energy when m lowers by h, we get mgh=12mv2+(12Mv2CM+12Iω2)
=12mv2+(12Mv2CM+12×12MR2v2CMR2)
=12mv2+34Mv2CM
=12mv2+34Mv2(RR−r)
v2=4mgh2m+3M[RR−r]2
Comparing with v2=2ah
a=v22h=2mg2m+3M[R/(R−r)]2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.413videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective19videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.213videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
two masses 2m and m are attached to the the ends of a string while passing over a smooth Pulley of mass m and radius R. The ratio of tensions in both the strings is
_PHY_E05_245_Q01.png) View Solution
View SolutionA block of mass m is attached at the end of an inextensible string which is wound over a rough pulley of mass M and radius R figure a. Assume the string does not slide over the pulley. Find the acceleration of the block when released.
View SolutionTwo bodies of mass 4kg and 6kg are attached to the ends of a string passing over a pulley. The 4kg mass is attached to the table top by another string. The tension in this string T1 is equal to: Take
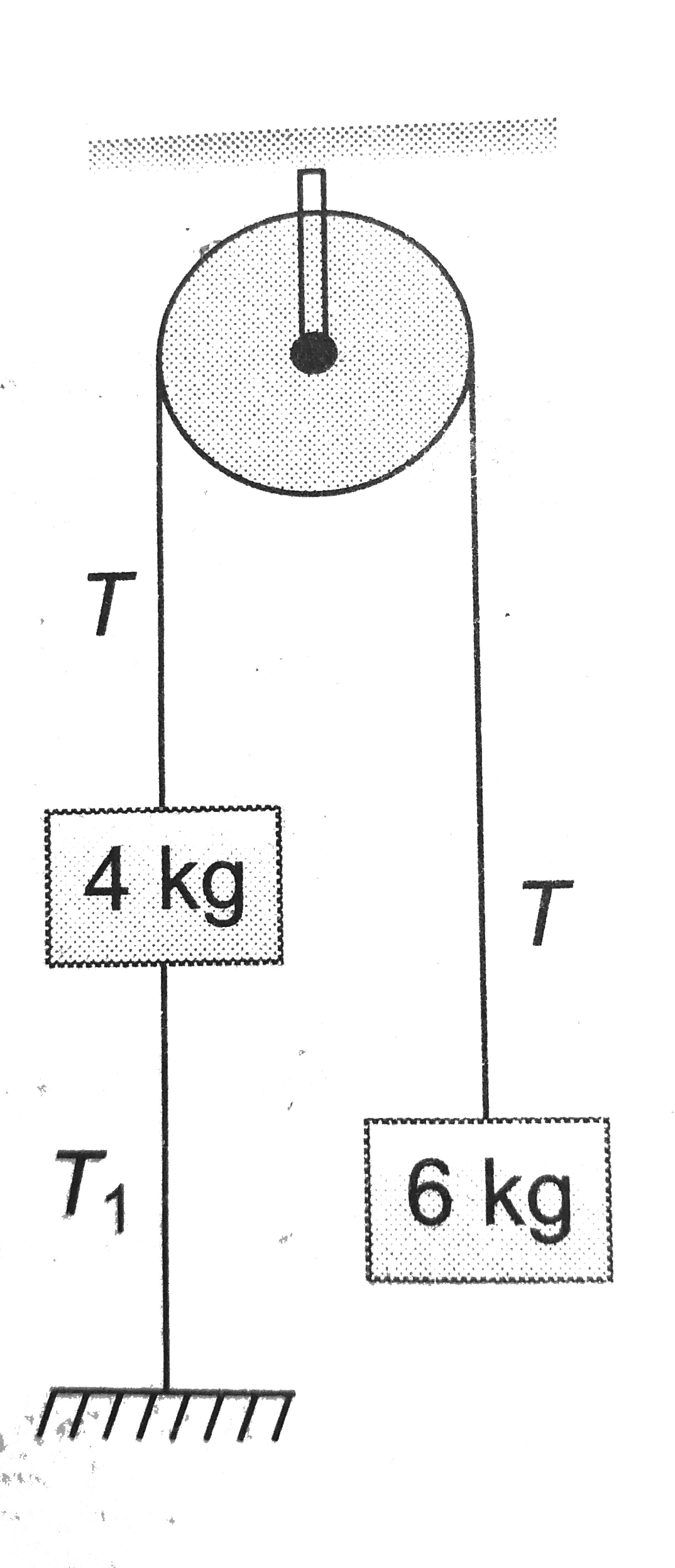 View Solution
View Solution
Consider the arrangement shown in figure. The string is wrapped around a uniform cylinder which rolls without slipping. The other end of the string is passed over a masslessm frictionless pulley to a falling weight, determine the acceleration of the falling mass m in terms of only the mass of the cylinder M, the mass m and gView SolutionA spool of mass M and radius 2R lies on an inclined plane as shown in the figure. A light thread is wound around the connecting tube of the spool and its free end carries a weight of mass m. The value of m so that system is in equilibrium is
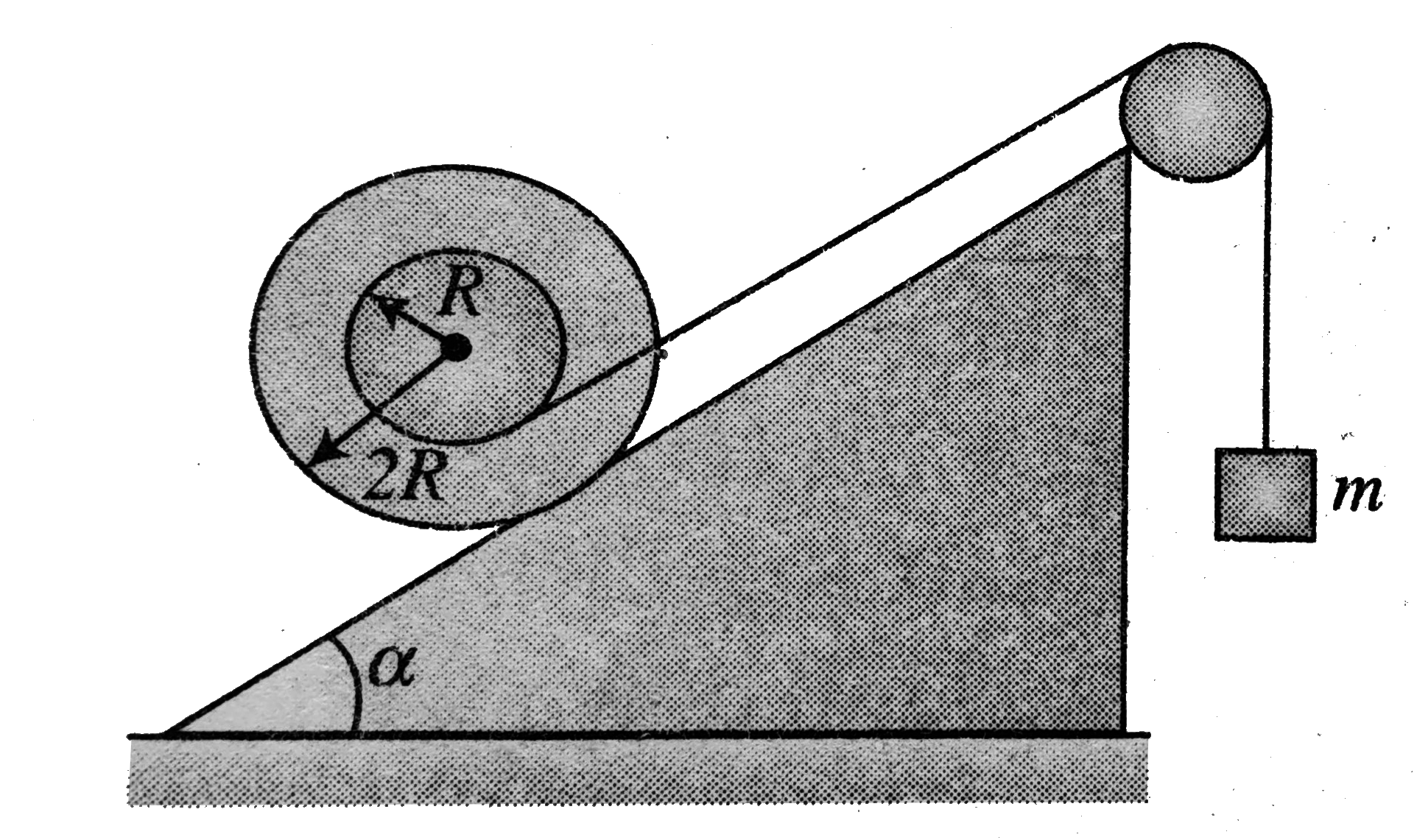 View Solution
View SolutionTwo unequal masses are connected by a very light string over a clamped light smooth pulley. Find the acceleration of the system and the tension in the string.
View SolutionA disc of mass M has a light, thin string wrapped several times around its circumference. The free end of string is attaced to the ceiling and the disc is released from rest. Find the acceleration of the disc and the tension in the string.
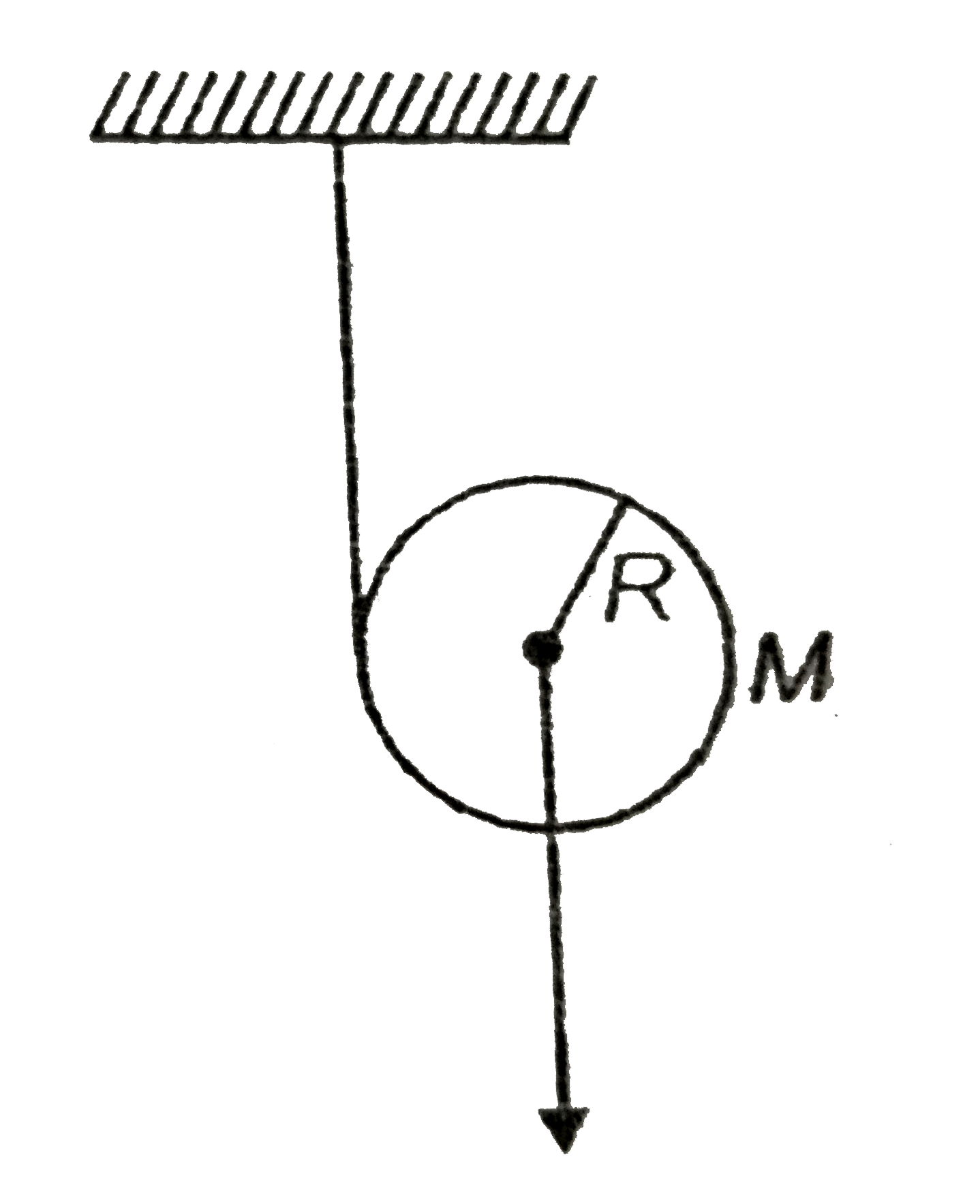 View Solution
View SolutionTwo blocks of masses 6kg and 4kg are attached to the two ends of a massless string passing over a smooth fixed pulley. if the system is released, the acceleration of the centre of mass of the system will be
View SolutionA body of mass 20 kg is resting on a table. A light string is attached to it and passed over a smooth pulley at the edge of the table and a mass 3kg is attached at the free end. What is the acceleration of the system of the coefficient of kinetic friction between the mass and the table is 0.04 ? What is the tension in the string ?
View SolutionTwo blocks of masses 2 kg and 4 kg are connected by a light string passing over a light smooth pulley clamped to the edge of a horizontal table. The 2 kg block is on the smooth horizontal table and the other block is hanging vertically, (i) Find the acceleration of the stem if it is released from rest, (ii) Find the tension in the string.
View Solution
