Two unequal masses are connected by a very light string over a clamped light smooth pulley. Find the acceleration of the system and the tension in the string.
To solve the problem of two unequal masses connected by a light string over a smooth pulley, we will follow these steps:
Step 1: Identify the masses and forces
Let the two masses be m1 and m2, where m1>m2. The gravitational force acting on each mass is given by:
- For m1: Fg1=m1g
- For m2: Fg2=m2g
Step 2: Set up the equations of motion
Since m1 is greater than m2, m1 will move downward while m2 will move upward. We can write the equations of motion for both masses:
1. For m1:
m1g−T=m1a(1)
2. For m2:
T−m2g=m2a(2)
Where T is the tension in the string and a is the acceleration of the system.
Step 3: Solve the equations for acceleration
From equation (1), we can express T:
T=m1g−m1a(3)
From equation (2), we can express T as well:
T=m2g+m2a(4)
Now, we can set equations (3) and (4) equal to each other:
m1g−m1a=m2g+m2a
Rearranging gives:
m1g−m2g=m1a+m2a
Factoring out g and a:
(m1−m2)g=(m1+m2)a
Now, we can solve for a:
a=(m1−m2)g(m1+m2)(5)
Step 4: Substitute a back to find tension T
Now we can substitute a back into either equation (3) or (4) to find T. Let's use equation (3):
T=m1g−m1((m1−m2)g(m1+m2))
This simplifies to:
T=m1g(1−(m1−m2)(m1+m2))
Combining the fractions:
T=m1g((m1+m2)−(m1−m2)(m1+m2))
T=m1g(2m2(m1+m2))
T=2m1m2g(m1+m2)(6)
Final Results
Thus, the acceleration a of the system is given by:
a=(m1−m2)g(m1+m2)
And the tension T in the string is given by:
T=2m1m2g(m1+m2)
Let the two masses be m1 and m2, where m1>m2. The gravitational force acting on each mass is given by:
- For m1: Fg1=m1g
- For m2: Fg2=m2g
Since m1 is greater than m2, m1 will move downward while m2 will move upward. We can write the equations of motion for both masses:
m1g−T=m1a(1)
T−m2g=m2a(2)
From equation (1), we can express T:
T=m1g−m1a(3)
T=m2g+m2a(4)
m1g−m1a=m2g+m2a
m1g−m2g=m1a+m2a
(m1−m2)g=(m1+m2)a
a=(m1−m2)g(m1+m2)(5)
Now we can substitute a back into either equation (3) or (4) to find T. Let's use equation (3):
T=m1g−m1((m1−m2)g(m1+m2))
T=m1g(1−(m1−m2)(m1+m2))
T=m1g((m1+m2)−(m1−m2)(m1+m2))
T=m1g(2m2(m1+m2))
T=2m1m2g(m1+m2)(6)
Thus, the acceleration a of the system is given by:
a=(m1−m2)g(m1+m2)
T=2m1m2g(m1+m2)
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - SHORT ANSWER TYPE QUESTION
7 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
13 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
10 Videos
- LOGIC GATESBOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)
10 Videos
Similar Questions
Two bodies of masses 1 kg and 2 kg are connected by a very light string passed over a clamped light smooth pulley. If the system is released from rest, find the acceleration of the two masses and the tension in the string
View SolutionTwo masses of 3 kg and 4 kg are connected at the two ends of a light inextensible string that passes over a frictionless pulley. Find the acceleration of the masses and the tension in the string, when the masses are released.
View Solution
Knowledge Check
Two masses 8 kg and 12 kg are connected at the two ends of a light in extensible string that passes over a friction less pulley Find the acceleration of the masses and tension in the string , when the masses are released
 . Ag4Bg5Cg8Dg6
. Ag4Bg5Cg8Dg6
Two unequal masses of 1kg and 2kg are connected by a string going over a clamed light smooth pulley as shown in figure . The system is released from rest .The larger mass is stopped for a moment 1.0s after the system is set in motion.Find the time elapsed before the string is tight again.

View SolutionTwo masses 8 kg and 12 kg are connected at the two ends of a light in extensible string that passes over a friction less pulley. Find the acceleration of the masses and tension in the string , when the masses are released
 .
.
View SolutionIn a simple Atwood machine, two unequal masses m1andm2 are connected by string going over a clamped light smooth pulley . In a typical arrangement m1=300g and m2=600g. The system is released from rest. (a) Find the distance travelled by the first block in first two seconds. (b) Find the tension in the string. (c) Find the force exerted by clamp on the pulley.
View SolutionThe strings are inextensible and light: the pulleys are smooth and light. Find the acceleration of each block and tensions in the strings.

View SolutionTwo masses 2 kg and 4 kg are connected at the two ends of light inextensible string passing over a frictionless pulley. If the masses are released, then find the acceleration of the masses and the tension in the string.
View SolutionTwo masses 2 kg and 4 kg are connected at two ends of light inextensible string passing over a frictionless pulley . If the masses are released , then find the accelaration of the masses and the tension in the string .
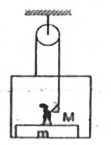
View SolutionA man of mass M is standing on a plank kept in a box. The plank and box as a whole has mass m. A light string passing over a fixed smooth pulley connects the man and box. If the box remains stationary, find the tension in the string and the force exerted by the man on the plank.
View Solution
