A spring is cut into two halves. What happens to its period of oscillation of a mass suspended from it, before cutting and after cutting ?
To solve the problem of what happens to the period of oscillation of a mass suspended from a spring when the spring is cut into two halves, we can follow these steps:
Step 1: Understand the formula for the period of oscillation
The period of oscillation T for a mass m attached to a spring with spring constant k is given by the formula:
T=2π√mk
Step 2: Identify the initial conditions
Before cutting the spring, we have:
- Spring constant: k
- Period of oscillation:
T1=2π√mk
Step 3: Analyze the effect of cutting the spring
When the spring is cut into two equal halves, the length of each half is reduced by half. The spring constant k is inversely proportional to the length of the spring. Therefore, if the length is halved, the new spring constant k2 becomes:
k2=2k
Step 4: Calculate the new period of oscillation
After cutting the spring, the new period of oscillation T2 can be calculated using the new spring constant k2:
T2=2π√mk2=2π√m2k=2π√mk⋅1√2=T1⋅1√2
Step 5: Compare the periods
From the calculations:
- Before cutting: T1=2π√mk
- After cutting: T2=T1√2
This shows that the period of oscillation decreases after cutting the spring.
Conclusion
The period of oscillation of the mass suspended from the spring decreases after the spring is cut into two halves.
---
The period of oscillation T for a mass m attached to a spring with spring constant k is given by the formula:
T=2π√mk
Before cutting the spring, we have:
- Spring constant: k
- Period of oscillation:
T1=2π√mk
When the spring is cut into two equal halves, the length of each half is reduced by half. The spring constant k is inversely proportional to the length of the spring. Therefore, if the length is halved, the new spring constant k2 becomes:
k2=2k
After cutting the spring, the new period of oscillation T2 can be calculated using the new spring constant k2:
T2=2π√mk2=2π√m2k=2π√mk⋅1√2=T1⋅1√2
From the calculations:
- Before cutting: T1=2π√mk
- After cutting: T2=T1√2
The period of oscillation of the mass suspended from the spring decreases after the spring is cut into two halves.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - LONG ANSWER QUESTIONS3videos
OSCILLATIONS
- BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SHORT ANSWER QUESTIONS47videos
OSCILLATIONS
- BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - ADDITIONAL SOLVED PROBLEMS11videos
OSCILLATIONS
- BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - SELECTED PROBLEMS (FROM POISEUILLE.S FORMULA)19videos
MOTION IN FLUIDS
- BOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 4 ( TEMPERATURE ) UNSOLVED PROBLEMS12videos
PROPERTIES OF MATTER
Similar Questions
Knowledge Check
- Question 1 - Select One
If the period of oscillation of mass M suspended. From a spring is one second, then the period of 4 M will be
A1/2B1/4 secC2 secD4 sec
The ratio of the time periods of small oscillation of the insulated spring and mass system before and after charging the masses is
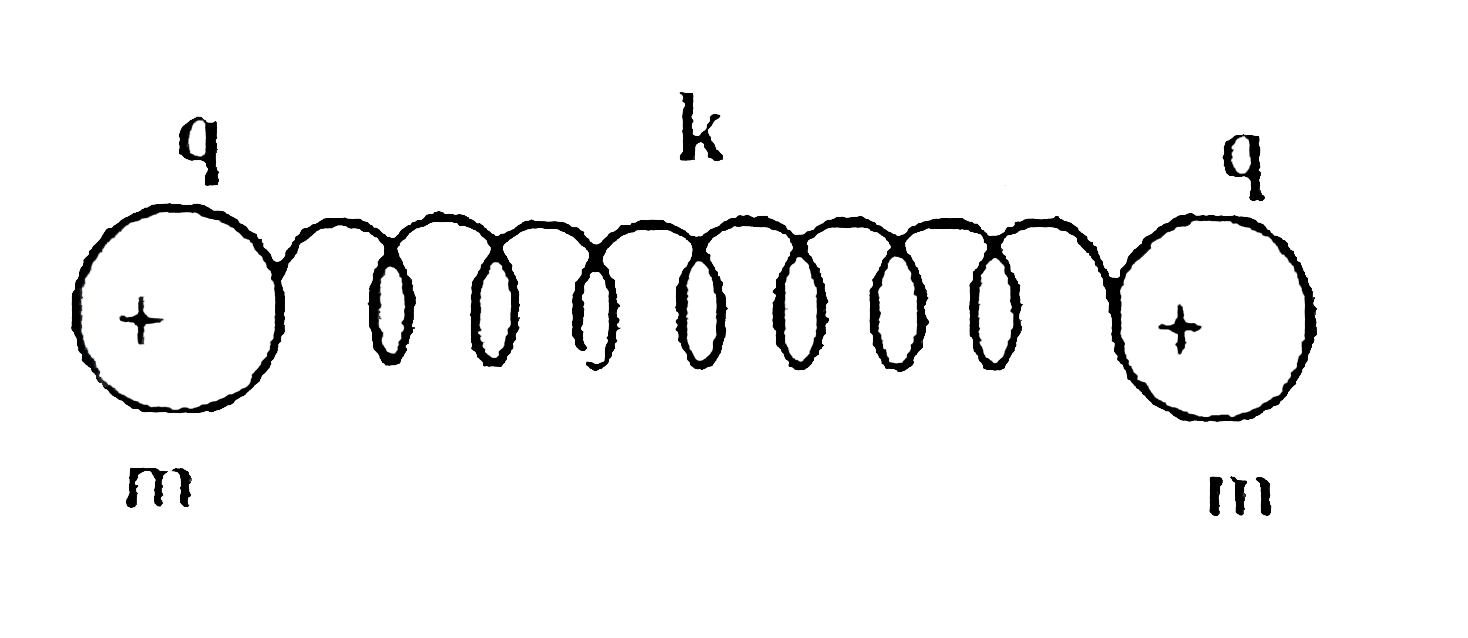 View Solution
View SolutionPeriodic time of oscillation T1 is obtained when a mass is suspended from a spring and if another spring is used with same mass then periodic time of oscillation is T2 . Now if this mass is suspended from series combination of above springs then calculated the time period.
View SolutionA mass m is suspended from a spring. Its frequency of oscillation is f. The spring is cut into two halves and the same mass is suspended from one of the pieces of the spring. The frequency of oscillation of the mass will be
View SolutionA spring has a certain mass suspended from it and its period for vertical oscillations is T1. The spring is now cut into two equal halves and the same mass is suspended from one of the half. The period of vertical oscillation is now T2. The ratio of T2/T1 is
View SolutionA weightless spring has a force constant k oscillates with frequency f when a mass m is suspended from it The spring is cut into three equal parts and a mass 3 m is suspended from it The frequency of oscillation of one part will now become
View SolutionAn object suspended from a spring exhibits oscillations of period T. Now the spring is cut in two halves and the same object is suspended with two halves as shown in figure. The new time period of oscillation will become
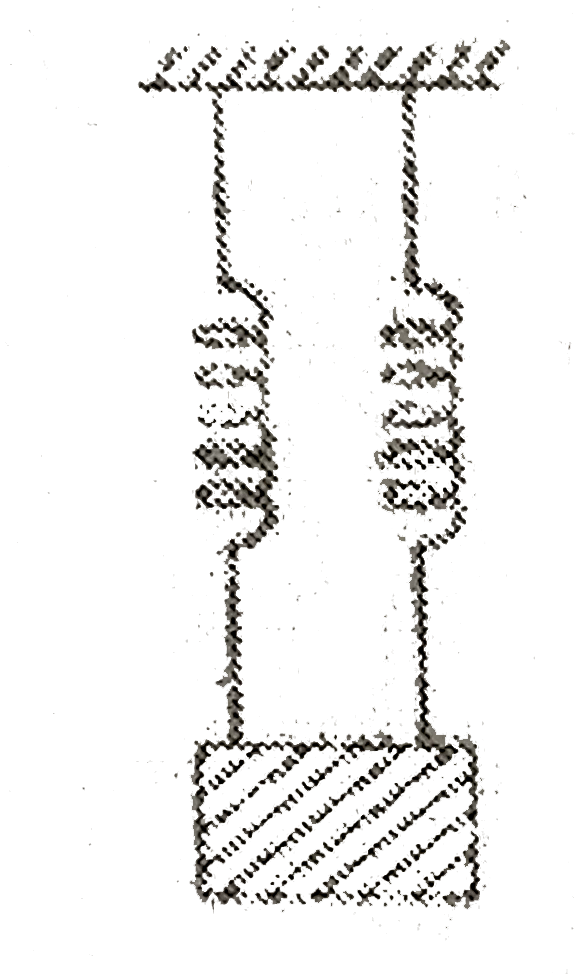 View Solution
View SolutionThe time period of a mass suspended from a spring is T. If the spring is cut into four equal parts and the same mass is suspended from one of the parts, then the new time period will be
View Solution

