Draw the velocity-displacement graph of a body executing shm.
To draw the velocity-displacement graph of a body executing Simple Harmonic Motion (SHM), we can follow these steps:
1. Understand the Equation of Velocity in SHM:
The velocity v of a body executing SHM is given by the equation:
v=ω√A2−x2
where ω is the angular frequency, A is the amplitude, and x is the displacement.
2. Square the Velocity Equation:
To simplify the graphing process, square both sides of the equation:
v2=ω2(A2−x2)
3. Rearrange the Equation:
Rearranging the equation gives:
v2=ω2A2−ω2x2
This can be rewritten as:
v2ω2+x2A2=1
4. Identify the Form of the Equation:
The equation v2ω2+x2A2=1 represents an ellipse in the v-x plane.
5. Determine the Axes:
- The y-axis represents the velocity v.
- The x-axis represents the displacement x.
- The maximum value of v occurs when x=0, which is v=ωA (the amplitude of the velocity).
- The maximum displacement occurs when v=0, which is x=A.
6. Plot the Graph:
- The graph will be an ellipse with:
- The y-intercept at v=ωA (when x=0).
- The x-intercept at x=A (when v=0).
- The shape of the ellipse will be symmetric about both axes.
7. Label the Graph:
Clearly label the axes and the intercepts to indicate the maximum values of velocity and displacement.
Final Graph:
The final graph will show an ellipse with:
- The vertical axis (y-axis) labeled as v (velocity).
- The horizontal axis (x-axis) labeled as x (displacement).
- The ellipse will touch the y-axis at v=ωA and the x-axis at x=A.
The velocity v of a body executing SHM is given by the equation:
v=ω√A2−x2
where ω is the angular frequency, A is the amplitude, and x is the displacement.
To simplify the graphing process, square both sides of the equation:
v2=ω2(A2−x2)
Rearranging the equation gives:
v2=ω2A2−ω2x2
This can be rewritten as:
v2ω2+x2A2=1
The equation v2ω2+x2A2=1 represents an ellipse in the v-x plane.
- The y-axis represents the velocity v.
- The x-axis represents the displacement x.
- The maximum value of v occurs when x=0, which is v=ωA (the amplitude of the velocity).
- The maximum displacement occurs when v=0, which is x=A.
- The graph will be an ellipse with:
- The y-intercept at v=ωA (when x=0).
- The x-intercept at x=A (when v=0).
- The shape of the ellipse will be symmetric about both axes.
Clearly label the axes and the intercepts to indicate the maximum values of velocity and displacement.
The final graph will show an ellipse with:
- The vertical axis (y-axis) labeled as v (velocity).
- The horizontal axis (x-axis) labeled as x (displacement).
- The ellipse will touch the y-axis at v=ωA and the x-axis at x=A.
Topper's Solved these Questions
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - LONG ANSWER QUESTIONS
3 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SHORT ANSWER QUESTIONS
47 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - ADDITIONAL SOLVED PROBLEMS
11 Videos
- MOTION IN FLUIDS BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - SELECTED PROBLEMS (FROM POISEUILLE.S FORMULA)
19 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 4 ( TEMPERATURE ) UNSOLVED PROBLEMS
12 Videos
Similar Questions
Draw the displacement-time, velocity-time and acceleration-time graph of a body executing shm.
View SolutionDraw graph showing the variation of displacement with time of a body executing (i) free oscillation (ii) damped oscillations.
View SolutionThe figure shows the displacement-time graph of a particle executing SHM. If the time period of oscillation is 2s, then the equation of motion is given by
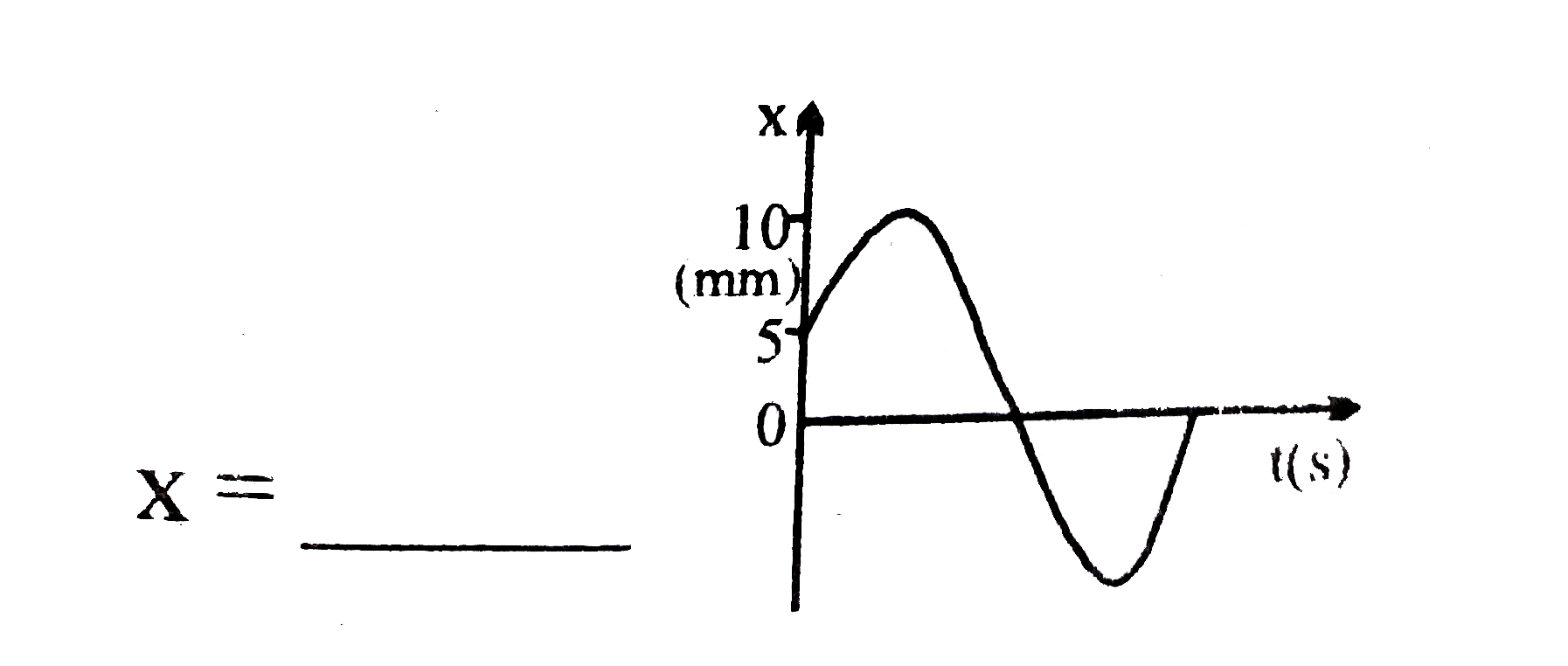
View SolutionThe figure shows the displacement-time graph of a particle executing SHM. If the time period of oscillation is 2s, then the equation of motion is given by
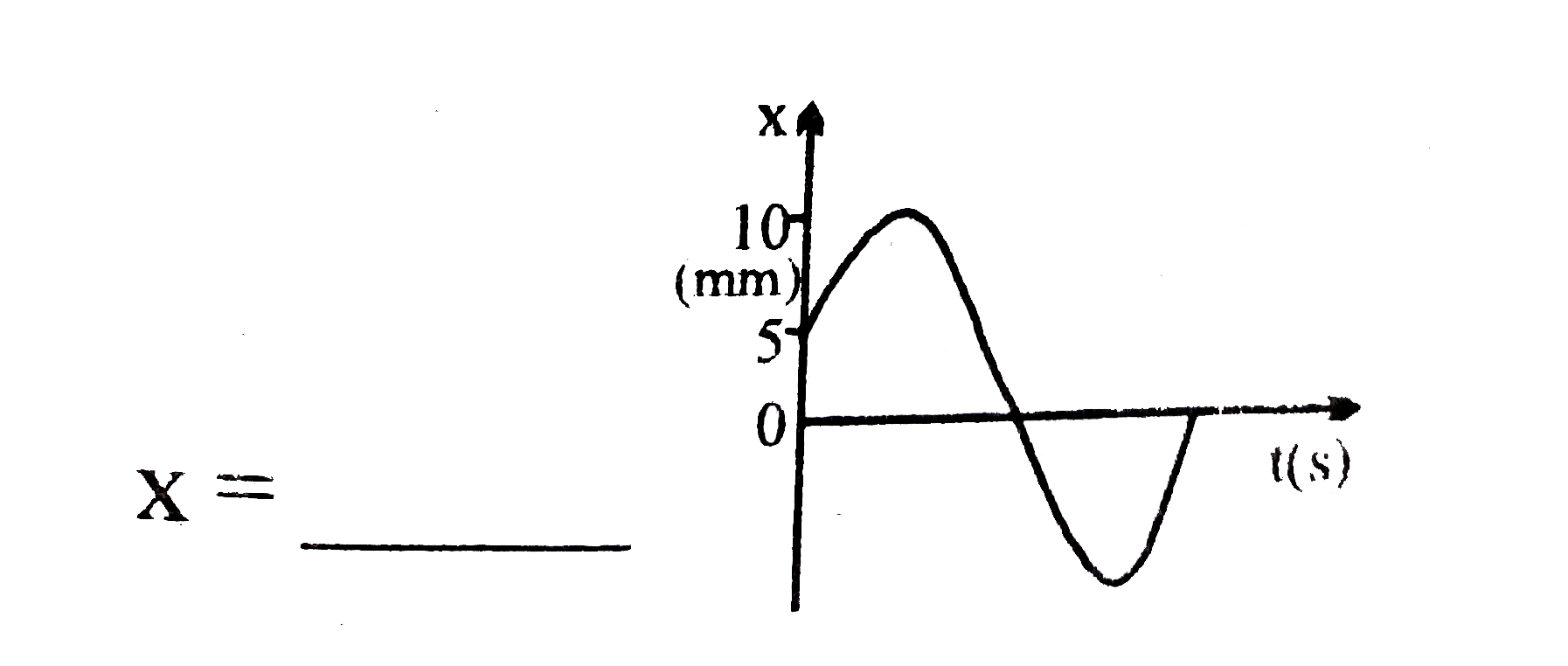
View SolutionThe figure below shows the velocity-time graph of a body moving in a straight line.
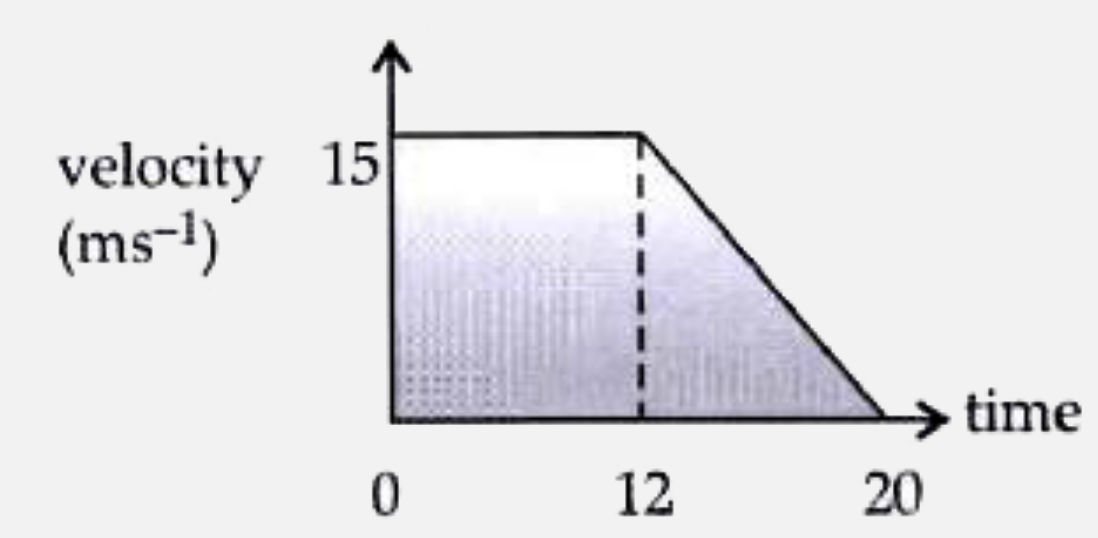
Find the total displacement of the body.
View SolutionDraw a graph between displacement and time for a body executing natural vibrations.
View SolutionWrite down the differential equation of a body executing shm. Give its solution.
View SolutionThe velocity time graph of a particle executing SHM is shown. The maximum acceleration of the particle is nπm/s2, where n is______.
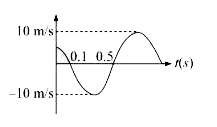
View SolutionDraw the shape of the velocity-time graph for a body moving with (a) uniform velocity, (b) uniform acceleration.
View SolutionIf a graph is plotted between velocity (v) and displacement (y) of a particle executing SHM from mean position, then the nature of the graph is
View Solution
