How will you determine the period of oscillation of a mass without the use of a clock? You are given a weightless spring, a metre scale and a known mass.
To determine the period of oscillation of a mass attached to a weightless spring without using a clock, we can follow these steps:
1. Set Up the Experiment:
- Hang the weightless spring from a fixed point (like a ceiling) using a suitable support. Ensure that the spring is vertical and can oscillate freely.
2. Attach the Known Mass:
- Attach the known mass (let's call it m) to the end of the spring. Make sure the mass is securely attached.
3. Measure the Stretch of the Spring:
- Allow the mass to come to rest. The mass will stretch the spring downwards. Measure the distance x that the spring stretches from its original length to the new equilibrium position.
4. Apply Hooke’s Law:
- According to Hooke's Law, the force exerted by the spring is given by F=kx, where k is the spring constant and x is the extension of the spring.
5. Balance Forces at Equilibrium:
- At equilibrium, the downward force due to the weight of the mass (mg) is balanced by the upward force exerted by the spring (kx). Thus, we can write:
mg=kx
6. Rearrange to Find the Ratio:
- Rearranging the equation gives:
mk=xg
- Here, g is the acceleration due to gravity.
7. Substitute into the Time Period Formula:
- The formula for the period of oscillation T of a mass-spring system is given by:
T=2π√mk
- Substitute mk from the previous step:
T=2π√xg
8. Calculate the Period:
- Now, you can calculate the period T using the measured values of x (the stretch of the spring) and g (approximately 9.81m/s2 on the surface of the Earth).
Final Formula:
T=2π√xg
- Hang the weightless spring from a fixed point (like a ceiling) using a suitable support. Ensure that the spring is vertical and can oscillate freely.
- Attach the known mass (let's call it m) to the end of the spring. Make sure the mass is securely attached.
- Allow the mass to come to rest. The mass will stretch the spring downwards. Measure the distance x that the spring stretches from its original length to the new equilibrium position.
- According to Hooke's Law, the force exerted by the spring is given by F=kx, where k is the spring constant and x is the extension of the spring.
- At equilibrium, the downward force due to the weight of the mass (mg) is balanced by the upward force exerted by the spring (kx). Thus, we can write:
mg=kx
- Rearranging the equation gives:
mk=xg
- Here, g is the acceleration due to gravity.
- The formula for the period of oscillation T of a mass-spring system is given by:
T=2π√mk
- Substitute mk from the previous step:
T=2π√xg
- Now, you can calculate the period T using the measured values of x (the stretch of the spring) and g (approximately 9.81m/s2 on the surface of the Earth).
T=2π√xg
Topper's Solved these Questions
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - LONG ANSWER QUESTIONS
3 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SHORT ANSWER QUESTIONS
47 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - ADDITIONAL SOLVED PROBLEMS
11 Videos
- MOTION IN FLUIDS BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - SELECTED PROBLEMS (FROM POISEUILLE.S FORMULA)
19 Videos
- PROPERTIES OF MATTERBOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 4 ( TEMPERATURE ) UNSOLVED PROBLEMS
12 Videos
Similar Questions
Knowledge Check
If the period of oscillation of mass M suspended. From a spring is one second, then the period of 4 M will be
A1/2B1/4 secC2 secD4 sec
Write down the expression for the period of oscillation of a mass attached to (i) a horizontal spring and (ii) a vertical spring.
View SolutionHow will you explain temperature using kinetic theory?
View SolutionFind the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.

View SolutionIf the period of oscillation of mass M suspended from a spring is one second, then the period of 9M will be
View SolutionDerive an experession for the period of oscillation of a mass attached to a spring executing simple harmonic motion. Given that the period of oscillation depends on the mass m and the force constant k, where k is the force required to stretch the spring by unit length?
View SolutionObtain an expression for the period of oscillations of a mass attached to end of a spring and undergoing shm. Obtain expression for K.E. and P.E. at any position during shm.
View SolutionFind the time period of the oscillation of mass m in figure a,b,c what is the equivalent spring constant of the pair oif springs in each case?
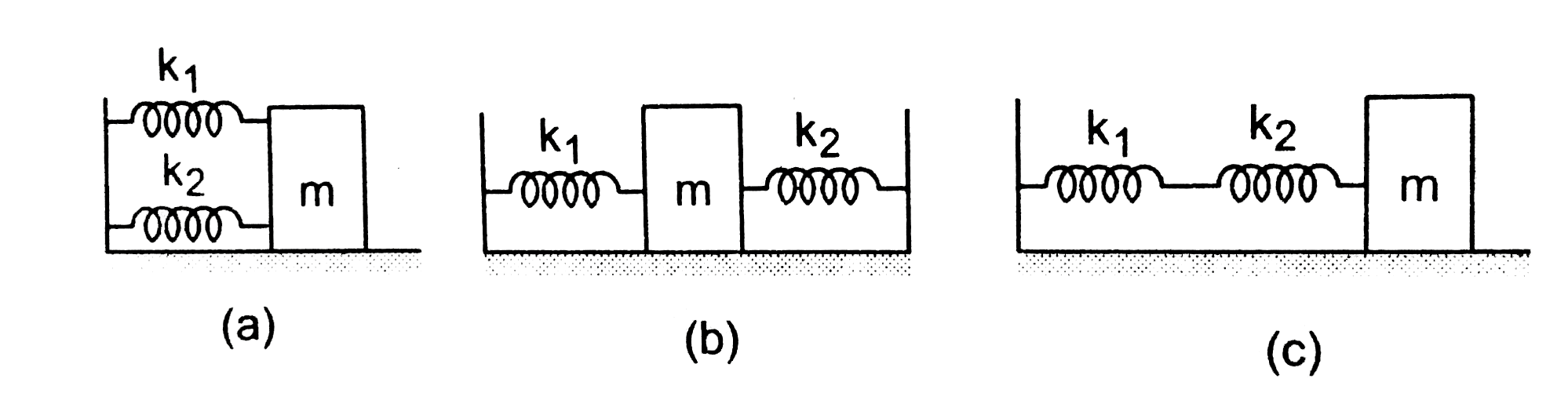
View Solution
