A spring is placed in vertical position by suspending it from a hook at its top. A similar hook on the bottom of the spring is at 11 cm above a table top. A mass of 75 g and of negligible size is then suspended from the bottom hook, which is measured to be 4.5 cm above the table top. The mass is then pulled down a distance of 4 cm and released. Find the approximate. Position of the bottom hook after 5 s? Take g=10ms2 and hook's mass to be negligible.
5 cm above the table top
4.5 cm above the table top
9 cm above the table top
0.5 cm above the table top
The correct Answer is:D
To solve the problem step by step, we will follow the outlined process below:
Step 1: Understand the Setup
- The spring is suspended vertically with a hook at the top.
- The bottom hook is positioned 11 cm above the tabletop.
- A 75 g mass is suspended from the bottom hook, which is measured to be 4.5 cm above the tabletop.
Step 2: Calculate the Initial Extension of the Spring
- The initial position of the mass is at 4.5 cm above the tabletop.
- The distance from the top hook to the bottom hook is 11 cm.
- Therefore, the initial extension x0 of the spring when the mass is at equilibrium is:
x0=11 cm−4.5 cm=6.5 cm=0.065 m
Step 3: Calculate the Weight of the Mass
- The mass m is given as 75 g, which is 0.075 kg.
- The weight W of the mass is calculated using:
W=mg=0.075 kg×10 m/s2=0.75 N
Step 4: Calculate the Spring Constant K
- At equilibrium, the weight of the mass is balanced by the spring force:
W=Kx0
Rearranging gives:
K=Wx0=0.75 N0.065 m≈11.54 N/m
Step 5: Calculate the Time Period of Oscillation
- The time period T of the oscillation is given by:
T=2π√mK
Substituting the values:
T=2π√0.075 kg11.54 N/m≈0.5 s
Step 6: Determine the Number of Complete Cycles in 5 Seconds
- The total time given is 5 seconds.
- The number of complete cycles n in 5 seconds is:
n=5 sT=5 s0.5 s=10
Step 7: Determine the Position After 5 Seconds
- Since the mass starts at its maximum displacement (pulled down 4 cm from the equilibrium position) and completes 10 full cycles, it returns to the equilibrium position.
- The equilibrium position of the mass is at 4.5 cm above the tabletop, meaning the bottom hook is at:
11 cm−4.5 cm=6.5 cm above the tabletop
Step 8: Final Position of the Bottom Hook
- After 5 seconds, the bottom hook will be at 6.5 cm above the tabletop.
Conclusion
The approximate position of the bottom hook after 5 seconds is 6.5 cm above the tabletop.
- The spring is suspended vertically with a hook at the top.
- The bottom hook is positioned 11 cm above the tabletop.
- A 75 g mass is suspended from the bottom hook, which is measured to be 4.5 cm above the tabletop.
- The initial position of the mass is at 4.5 cm above the tabletop.
- The distance from the top hook to the bottom hook is 11 cm.
- Therefore, the initial extension x0 of the spring when the mass is at equilibrium is:
x0=11 cm−4.5 cm=6.5 cm=0.065 m
- The mass m is given as 75 g, which is 0.075 kg.
- The weight W of the mass is calculated using:
W=mg=0.075 kg×10 m/s2=0.75 N
- At equilibrium, the weight of the mass is balanced by the spring force:
W=Kx0
Rearranging gives:
K=Wx0=0.75 N0.065 m≈11.54 N/m
- The time period T of the oscillation is given by:
T=2π√mK
Substituting the values:
T=2π√0.075 kg11.54 N/m≈0.5 s
- The total time given is 5 seconds.
- The number of complete cycles n in 5 seconds is:
n=5 sT=5 s0.5 s=10
- Since the mass starts at its maximum displacement (pulled down 4 cm from the equilibrium position) and completes 10 full cycles, it returns to the equilibrium position.
- The equilibrium position of the mass is at 4.5 cm above the tabletop, meaning the bottom hook is at:
11 cm−4.5 cm=6.5 cm above the tabletop
- After 5 seconds, the bottom hook will be at 6.5 cm above the tabletop.
The approximate position of the bottom hook after 5 seconds is 6.5 cm above the tabletop.
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
Mass suspended to a spring is pulled down by 2.5 cm and let go. The mass oscillates with an amplitude of
View SolutionHow valency of elements changes : Down the group from top the bottom
View SolutionA spring of force constant 600Nm−1 is mounted on a horizontal table. A mass of 1.5 kg is attached to the free end of the spring,pulled sideways to a distance of 2 cm and released . The speed of the mass when the spring is compressed by 1 cm is
View SolutionA spot is placed on the bottom of a slab made of transperent material of refractive index 1.5. The spot is viewed vertically from the top when it seems to be raised by 2 cm. Then, the height of the slab is
View SolutionA table-top measures 2 m 25 cm by 1 m 50 cm. What is the perimeter of the table-top?
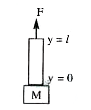
View SolutionA vertical force of magnitude Facts at the top of a string of mass 'm' and length 'l'. A body of mass M hangs at the bottom of the string.
View SolutionA coin at the bottom of a trough containing water to a depth of 15 cm appears to be 3.75 cm raised above from the bottom. Calculate the refractive index of water.
View SolutionA mass of 2kg suspended by string of mass 6kg. A wave of wavelength 6 cm is produced at bottom of string. Wavelength of wave at top end of string will be
View SolutionForce constant of a weightless spring is 16Nm−1. A body if mass 1 kg suspended from it is pulled down through 5 cm from its mean position and then released. The maximum kinetic energy of the body will be
View Solution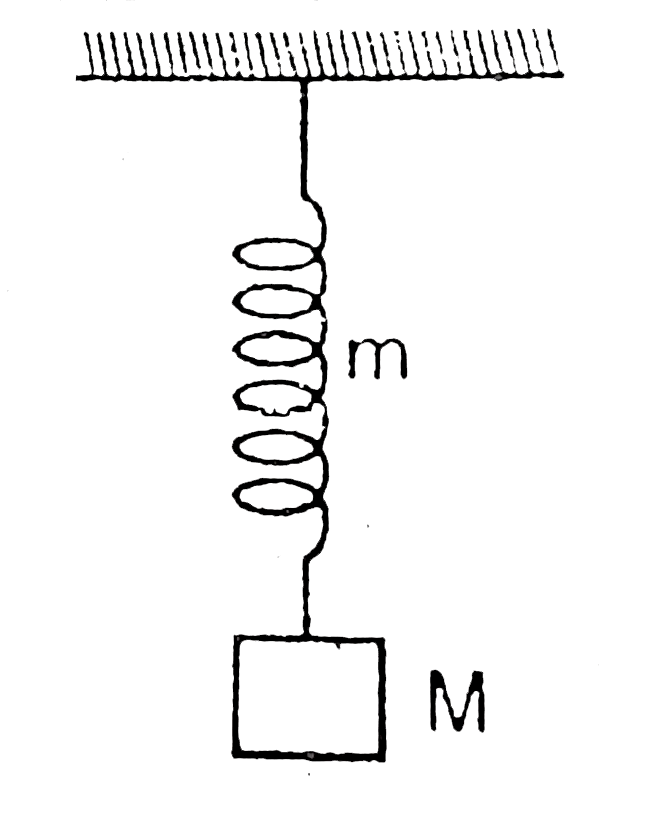
A block of M is suspended from a vertical spring of mass m as shown in the figure. When block is pulled down and released the mass oscillates with maximum velocity v.
View Solution
