A spring of force constant 800N/m has an extension of 5cm. The work done in extending it from 5cm to 15cm is
16 J
8 J
32 J
24 J
The correct Answer is:B
To find the work done in extending a spring from an extension of 5 cm to 15 cm, we can use the formula for the work done on a spring, which is given by:
W=12kx2
where:
- W is the work done,
- k is the spring constant,
- x is the extension of the spring from its natural length.
Step 1: Convert the extensions from cm to meters
First, we need to convert the extensions from centimeters to meters:
- Initial extension x1=5cm=0.05m
- Final extension x2=15cm=0.15m
Step 2: Calculate the work done at the final extension (15 cm)
Using the formula for work done:
W2=12kx22
Substituting the values:
W2=12×800N/m×(0.15m)2
W2=12×800×0.0225
W2=400×0.0225
W2=9J
Step 3: Calculate the work done at the initial extension (5 cm)
Now, calculate the work done at the initial extension:
W1=12kx21
Substituting the values:
W1=12×800N/m×(0.05m)2
W1=12×800×0.0025
W1=400×0.0025
W1=1J
Step 4: Calculate the work done in extending from 5 cm to 15 cm
The work done in extending the spring from 5 cm to 15 cm is given by:
W=W2−W1
Substituting the values:
W=9J−1J
W=8J
Final Answer
The work done in extending the spring from 5 cm to 15 cm is 8 joules.
---
- W is the work done,
- k is the spring constant,
- x is the extension of the spring from its natural length.
First, we need to convert the extensions from centimeters to meters:
- Initial extension x1=5cm=0.05m
- Final extension x2=15cm=0.15m
Using the formula for work done:
W2=12kx22
Substituting the values:
W2=12×800N/m×(0.15m)2
W2=12×800×0.0225
W2=400×0.0225
W2=9J
Now, calculate the work done at the initial extension:
W1=12kx21
Substituting the values:
W1=12×800N/m×(0.05m)2
W1=12×800×0.0025
W1=400×0.0025
W1=1J
The work done in extending the spring from 5 cm to 15 cm is given by:
W=W2−W1
Substituting the values:
W=9J−1J
W=8J
The work done in extending the spring from 5 cm to 15 cm is 8 joules.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - CHECK POINT 6.2
20 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - CHECK POINT 6.3
10 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - E Integer Type Questions
11 Videos
Similar Questions
A spring of force constant 800 N/m has an extension of 5 cm. The work done in extending it from 5 cm to 15 cm is:
View SolutionThe relationship between force and position is shown in the figure given (in one dimensional case). The work donw by the force in displacing a body from x=1cm to x=5cm is
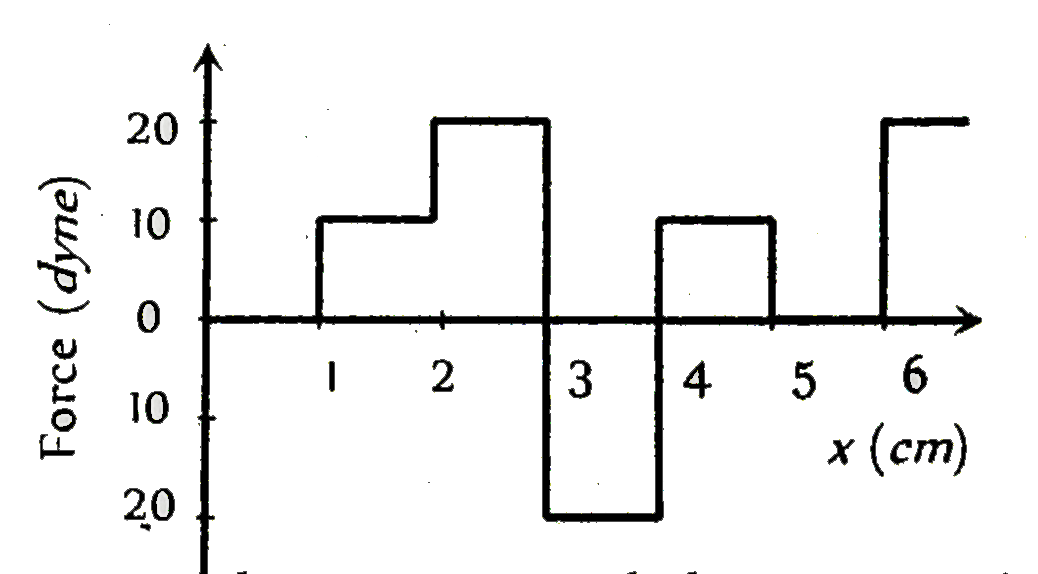
View SolutionFind the ratio of 90 cm to 1.5 m.
View SolutionA spring of force constant 600Nm−1 is mounted on a horizontal table. A mass of 1.5 kg is attached to the free end of the spring,pulled sideways to a distance of 2 cm and released . The speed of the mass when the spring is compressed by 1 cm is
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10 cm, then maximum speed of the trolley is
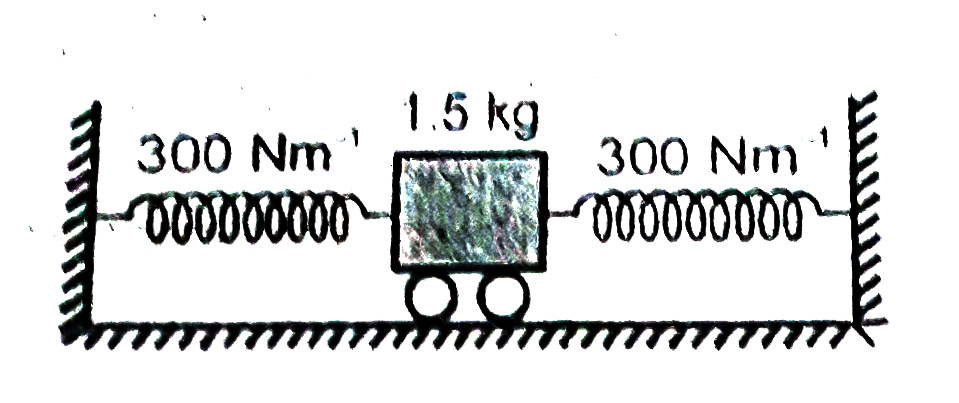
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is

View Solutiona block of mass 0.1 kg attached to a spring of spring constant400Nm pulled horizontally from x=0 tox1=10mm. Find the work done by the spring force
View SolutionA force F is exerted on a body of mass M, which is connected to a spring (spring constant k). The body has a constant acceleration a. Calculate the work done by the external force in moving the body by a distance D.
View SolutionA block of mass 4kg hangs from a spring of force constant k=400N/m. The block is pulled down 15cm below equilibrium and relesed. How long does it take block to go from 12cm below equilibrium (on the way up) to 9cm above equilibrium ?
View SolutionA block of mass 2kg is connected with a spring of natural length 40cm of force constant K=200N/m. The cofficient of friction is μ=0.5. When released from the given position, acceleration of block will be

View Solution
