A spring with one end attached to a mass and the other to a right support is stretched and released
Magnitude of acceleration, when just released is maximum
Magnitude of acceleration, when at equilibrium position, is maximum
Speed is maximum when is at equilibrium position
Magnitude of displacement is always maximum whenever speed is minimum
The correct Answer is:A, C
When spring is stretched by x, restoring force will be
Potential energy of the stretched spring
The restoring force is central hence, when particles relased it will executes SHM about equilibrium position.
Acceleration will be ,
At equilibrium position,
Hence, when just released ,
Hence, acceleration is maximum. Thus options (a) is correct
Hence, acceleration is maximum. Thus option (a) is correct.
At equilibrium whole PE will be converted to KE hence, KE will be maximum and hence, speed will be maximum.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE BOOK - NCERT EXEMPLARCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - Very Short Answer Type Qns
14 Videos
- MOTION IN A STRAIGHT LINE BOOK - NCERT EXEMPLARCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - Very Short Answer Type Qns
14 Videos
- MOTION IN A PLANEBOOK - NCERT EXEMPLARCHAPTER - MOTION IN A PLANEEXERCISE - Multiple Choice Questions
37 Videos
- OSCILLATIONSBOOK - NCERT EXEMPLARCHAPTER - OSCILLATIONSEXERCISE - MULTIPLE CHOICE QUESTIONS (MCQs)
40 Videos
Similar Questions
spring of force constant k clamped rigidly at onoe end and a mass m attached to its free end. A force F applied at the free end stretches the spring. Figure shows the same spring with both ends free and attached to a mass m at either end. Each end of the spring in figure is stretched by the same force F.
(a) What is the maximum extension of the spring in the two cases ?
(b) If the mass in figure and the two masses in figure are released free, what is the period of oscillation in each case?

View SolutionA disc of mass m2 is placed on a table. A stiff spring is attached to it and is vertical. The other end of the spring is attached to a disc of mass m1 What minimum force should be applied to the upper disc to press the spring such that the lower disc is lifted off the table when the external force is suddenly removed?

View Solution
Knowledge Check
When a mass m is hung on a spring, the spring stretched by 6 cm. If the loaded spring is pulled downward a little and released, then the period of vibration of the system will be
A0.27 sB0.35 sC0.49 sD0.64 s
Figure. (a) shows a spring of force constant k fixed at one end and carrying a mass m at the other end placed on a horizontal frictionless surface. The spring is stretched by a force F. Figure. (b) shows the same spring with both endsf free and a mass m fixed at each free end Each of the spring is streched by the same force F. The mass in case (a) and the masses in case (b) are then released. Which of the following statements are true?AWhile oscillating the maximum extension of the spring is more in case (a) than in case (b).BThe maximum extension of the spring is same in both cases.CThe time period of oscillation is the same in both cases.DThe time period of oscillation in case (a) is √2 time that in case (b).
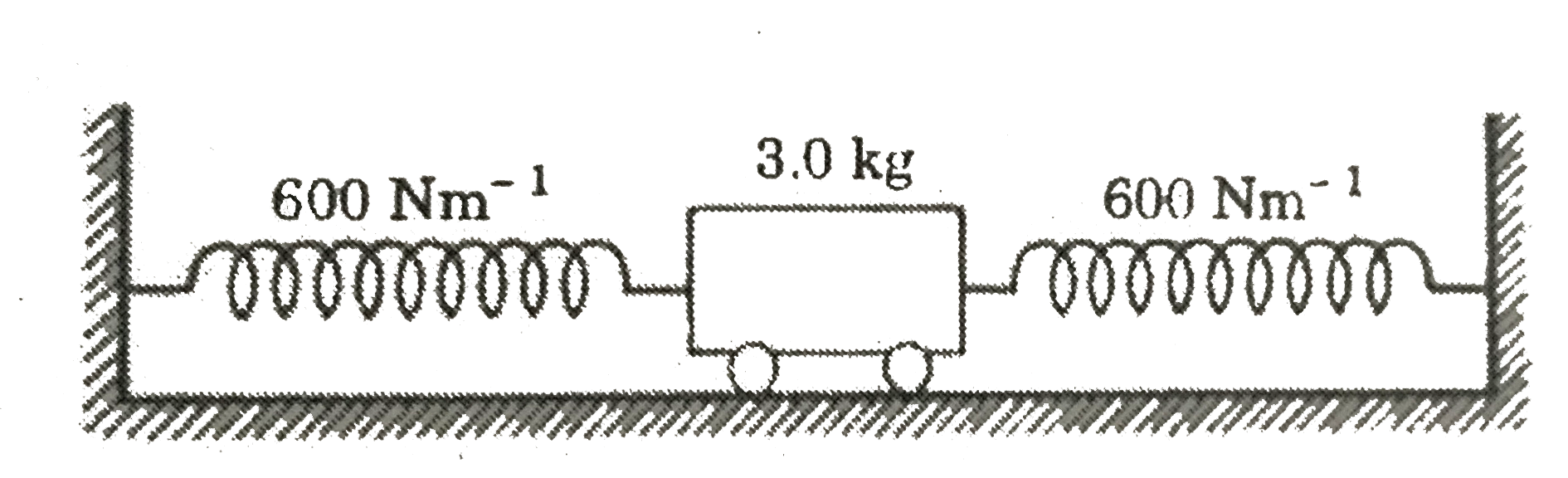
Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrium position by a distance x towards right, find the restoring force.

View SolutionTow identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrum position by a distance x towards right, find the restoring force.

View SolutionWhen a 20 N can is hung from the bottom of a vertical spring, it causes the spring to stretch 20 cm. The spring is now placed horizontal on a frictionless table. One end of it is held fixed, and the other end is attached to a 5.0 N can. The can is then moved (stretching the spring) and released from rest. What is the period (in×10−2s) of the resulting oscillation?
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View SolutionA string of length 40 cm and weighing 10 g is attached to a spring at one end and to a fixed wall at the other end. The spring has a spring constant of 160Nm−1 and is stretched by 1-0 cm. If a wave pulse is produced on the string near the wall, how much time will it take to reach the spring ?
View SolutionA certain spring stretches 25 cm when a 500 g mass is hung from its end. It is now used as shown in fig. With 2 kg mass at one end placed on a frictionless surface. Suppose the mass is pulled to the right until the spring is stretched to 10 cm and then released. find the speed with which the mass moves through the unstretched position.
View Solution
