A square plate of edge d and a circular disc of diameter d are placed toucing ech other at the midpoint of san edge of th plate as shown in figure. Locate the centre of mass of the combination assuming same mass per unit area for the two plates.
To locate the center of mass of the combination of a square plate and a circular disc, we can follow these steps:
Step 1: Understand the Problem
We have a square plate of edge length d and a circular disc with a diameter d. The disc is placed touching the square plate at the midpoint of one of its edges. We need to find the center of mass of this combination, assuming both have the same mass per unit area.
Step 2: Define Masses
Let the mass per unit area of both the square plate and the circular disc be σ.
- The area of the square plate is As=d2.
- The area of the circular disc is Ad=πd24.
Now, we can find the masses:
- Mass of the square plate:
Ms=σ⋅As=σ⋅d2
- Mass of the circular disc:
Md=σ⋅Ad=σ⋅πd24
Step 3: Set Up the Coordinate System
We will place the center of the square plate at the origin (0, 0). The center of the square plate is at (0, 0), and the midpoint of the edge where the disc touches is at (0, d2). The center of the circular disc will then be at (0, d).
Step 4: Calculate the Center of Mass
The coordinates of the center of mass (CM) for the system can be calculated using the formula:
xCM=Ms⋅xs+Md⋅xdMs+Md
yCM=Ms⋅ys+Md⋅ydMs+Md
Where:
- (xs,ys) is the center of the square plate (0, 0).
- (xd,yd) is the center of the circular disc (0, d).
Step 5: Calculate xCM
Since both centers have x-coordinates of 0:
xCM=Ms⋅0+Md⋅0Ms+Md=0
Step 6: Calculate yCM
Now substituting the values into the yCM formula:
yCM=Ms⋅0+Md⋅dMs+Md=Md⋅dMs+Md
Step 7: Substitute the Masses
Substituting the expressions for Ms and Md:
yCM=(σ⋅πd24)⋅dσ⋅d2+σ⋅πd24=πd34d2+πd24=πd34d2(1+π4)=πd41+π4
Step 8: Simplify
This simplifies to:
yCM=πd4+π
Final Result
Thus, the coordinates of the center of mass of the combination are:
(0,πd4+π)
We have a square plate of edge length d and a circular disc with a diameter d. The disc is placed touching the square plate at the midpoint of one of its edges. We need to find the center of mass of this combination, assuming both have the same mass per unit area.
Let the mass per unit area of both the square plate and the circular disc be σ.
- The area of the circular disc is Ad=πd24.
- Mass of the square plate:
Ms=σ⋅As=σ⋅d2
- Mass of the circular disc:
Md=σ⋅Ad=σ⋅πd24
We will place the center of the square plate at the origin (0, 0). The center of the square plate is at (0, 0), and the midpoint of the edge where the disc touches is at (0, d2). The center of the circular disc will then be at (0, d).
The coordinates of the center of mass (CM) for the system can be calculated using the formula:
xCM=Ms⋅xs+Md⋅xdMs+Md
yCM=Ms⋅ys+Md⋅ydMs+Md
- (xs,ys) is the center of the square plate (0, 0).
- (xd,yd) is the center of the circular disc (0, d).
Since both centers have x-coordinates of 0:
xCM=Ms⋅0+Md⋅0Ms+Md=0
Now substituting the values into the yCM formula:
yCM=Ms⋅0+Md⋅dMs+Md=Md⋅dMs+Md
Substituting the expressions for Ms and Md:
yCM=(σ⋅πd24)⋅dσ⋅d2+σ⋅πd24=πd34d2+πd24=πd34d2(1+π4)=πd41+π4
This simplifies to:
yCM=πd4+π
Thus, the coordinates of the center of mass of the combination are:
(0,πd4+π)
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Question For short Answer
25 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -2
11 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -1
18 Videos
- CALORIMETRYBOOK - HC VERMA ENGLISHCHAPTER - CALORIMETRYEXERCISE - Short answer
9 Videos
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Question for short Answer
10 Videos
Similar Questions
A square lamina of side a and a circular lamina of diameter a are placed touching each other as shown in figure. Find distance of their centre of mass from point O, the centre of square.

View SolutionA circular plate of uniform thickness has a diameter fo 56cm. A circular portion of diameter 42 cm is removed from one edge of the plate as shown in figure. Find the position of the centre of mass of the remaining portion.
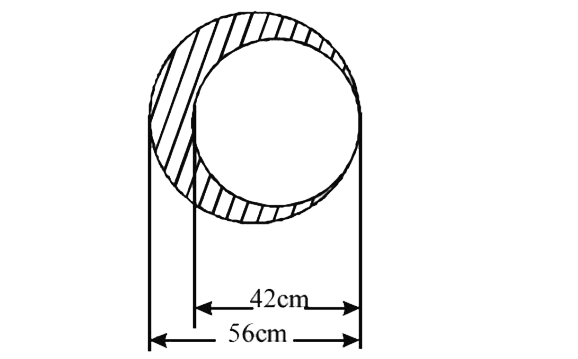
View SolutionFive uniform circular plates, each of diameter D and mass m are laid out in a pattern shown. Using the origin shown, find the y co-ordinate of the centre of mass of the five-plate system.
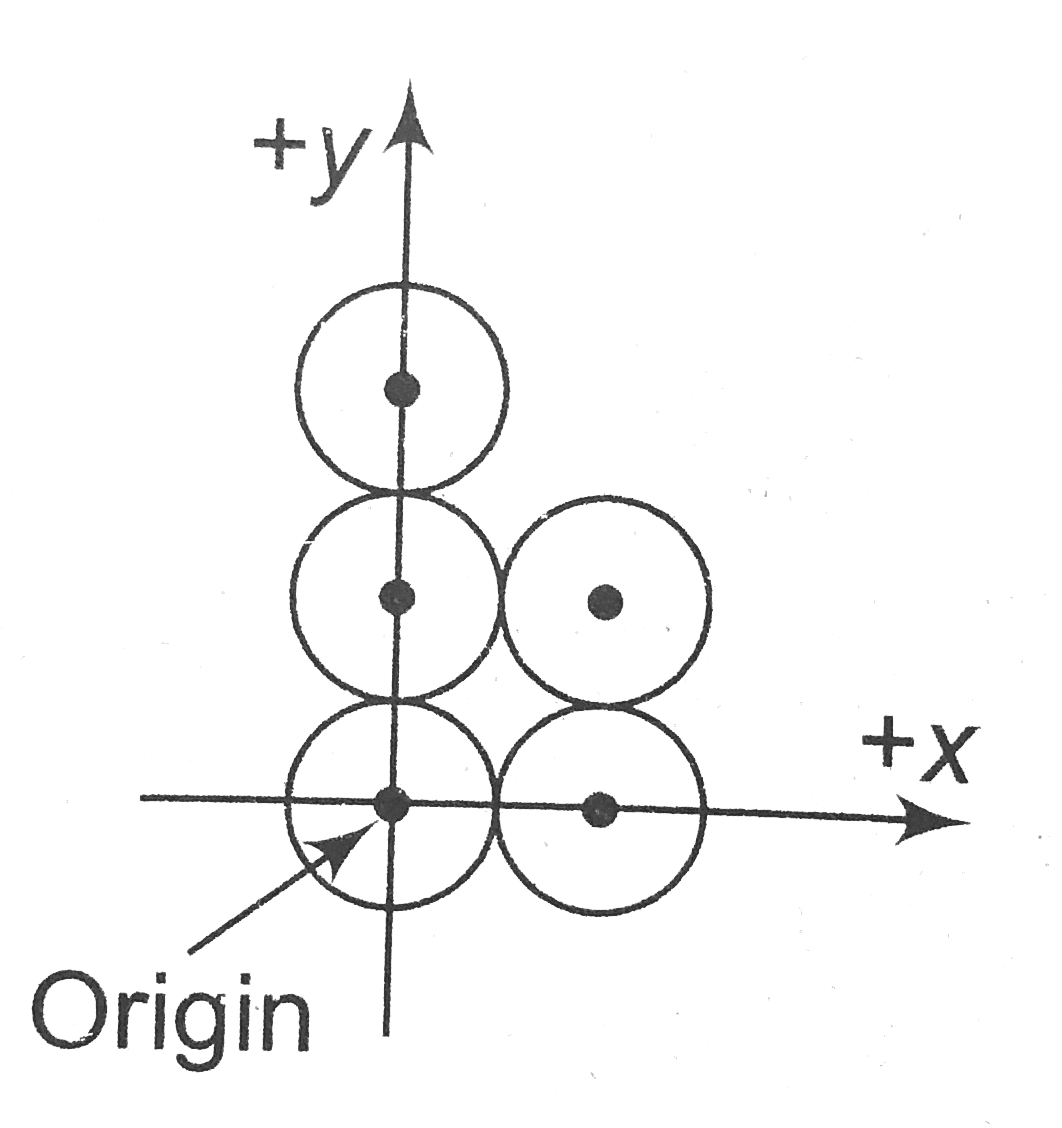 .
.
View SolutionA square plate of side 20cm has uniform thickness and density. A circular part of diameter 8cm is cut out symmetrically and shown in figure. The position of center of mass of the remaining potion is

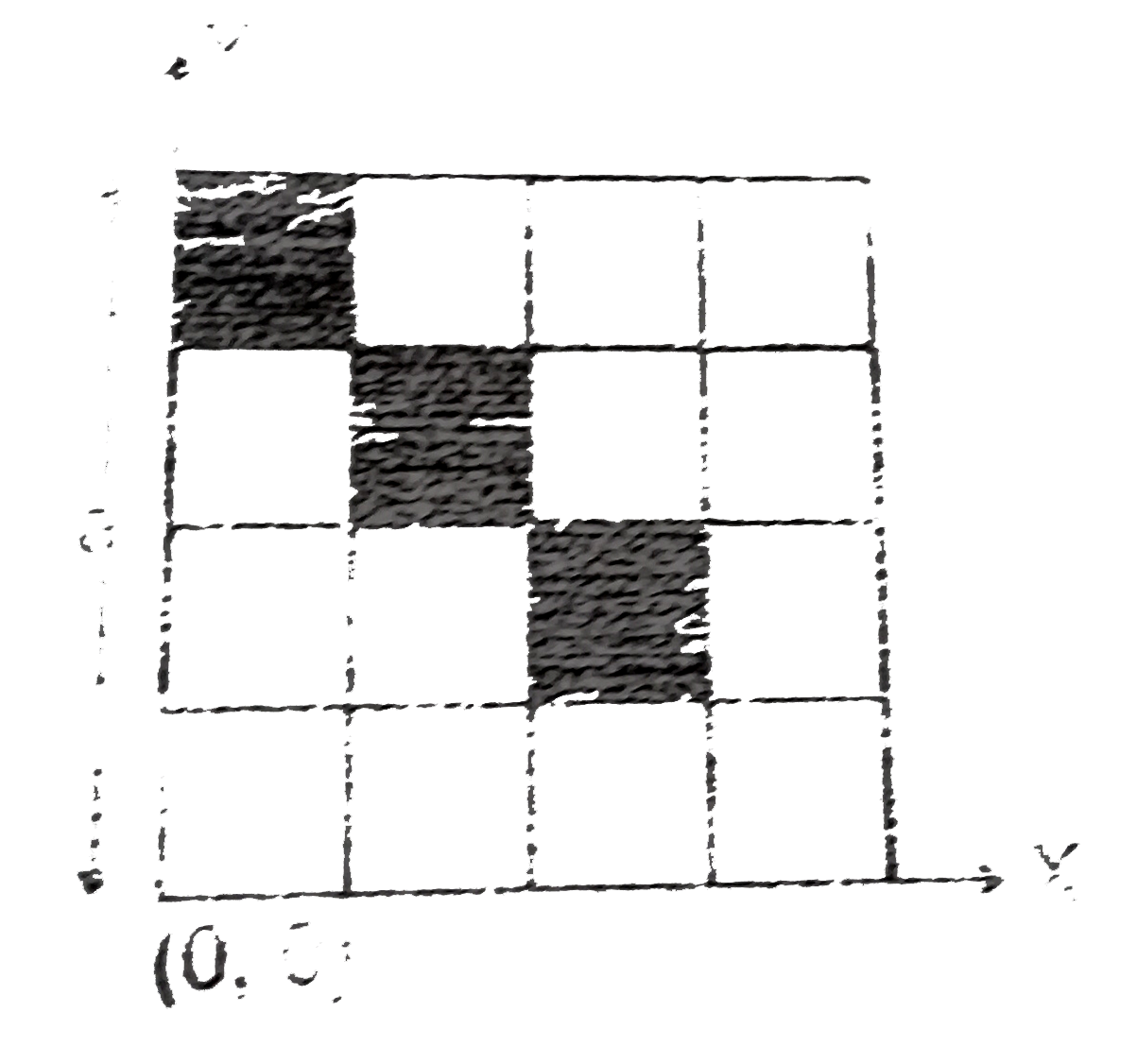
View SolutionFrom a uniform square plate the shaped portions are removed as shown in figure. The coordinates of centre of mass of the remaining plate are x,y Axes and origon are shown in figure.
View SolutionHalf of the recrtangular plate shown in figure is made of a material of density ρ1 and the other half of density ρ2. The length of the plate is L. Locate the centre of mass of the plate.

View SolutionA circular plate of diameter d is kept in contact with a square plate of edge d as shown in figure. The densit of the material and the thickness are same
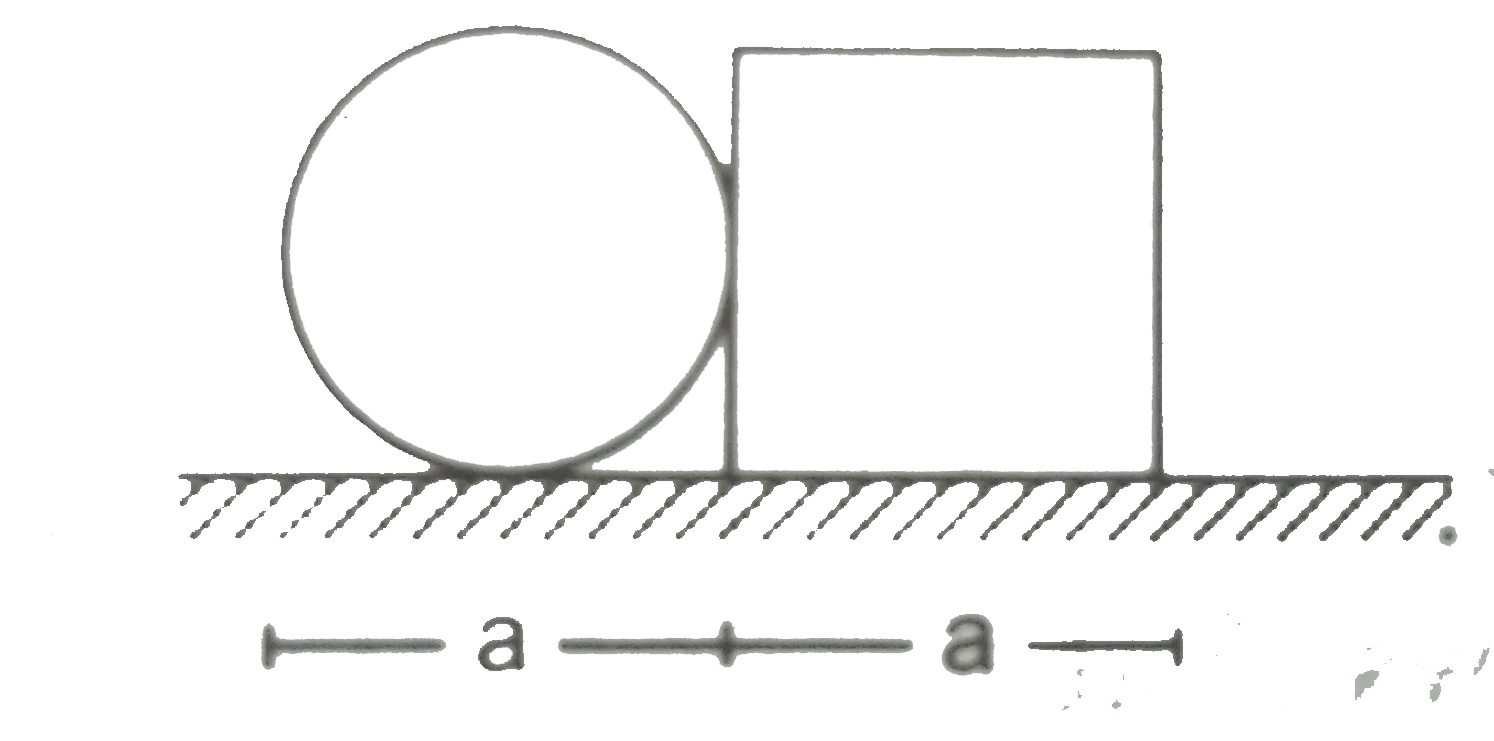 . Everywhere. The centre of mass of the composite system will be
. Everywhere. The centre of mass of the composite system will be
View SolutionA circular plate of diameter d is kept in contact with a square plate of edge d as shown in figure. The densit of the material and the thickness are same
 . Everywhere. The centre of mass of the composite system will be
. Everywhere. The centre of mass of the composite system will be
View SolutionA circular plate of diameter 'a' is kept in contact with a square plate of side a as shown. The density of the material and the thickness are same everywhere. The centre of mass of composite system will be
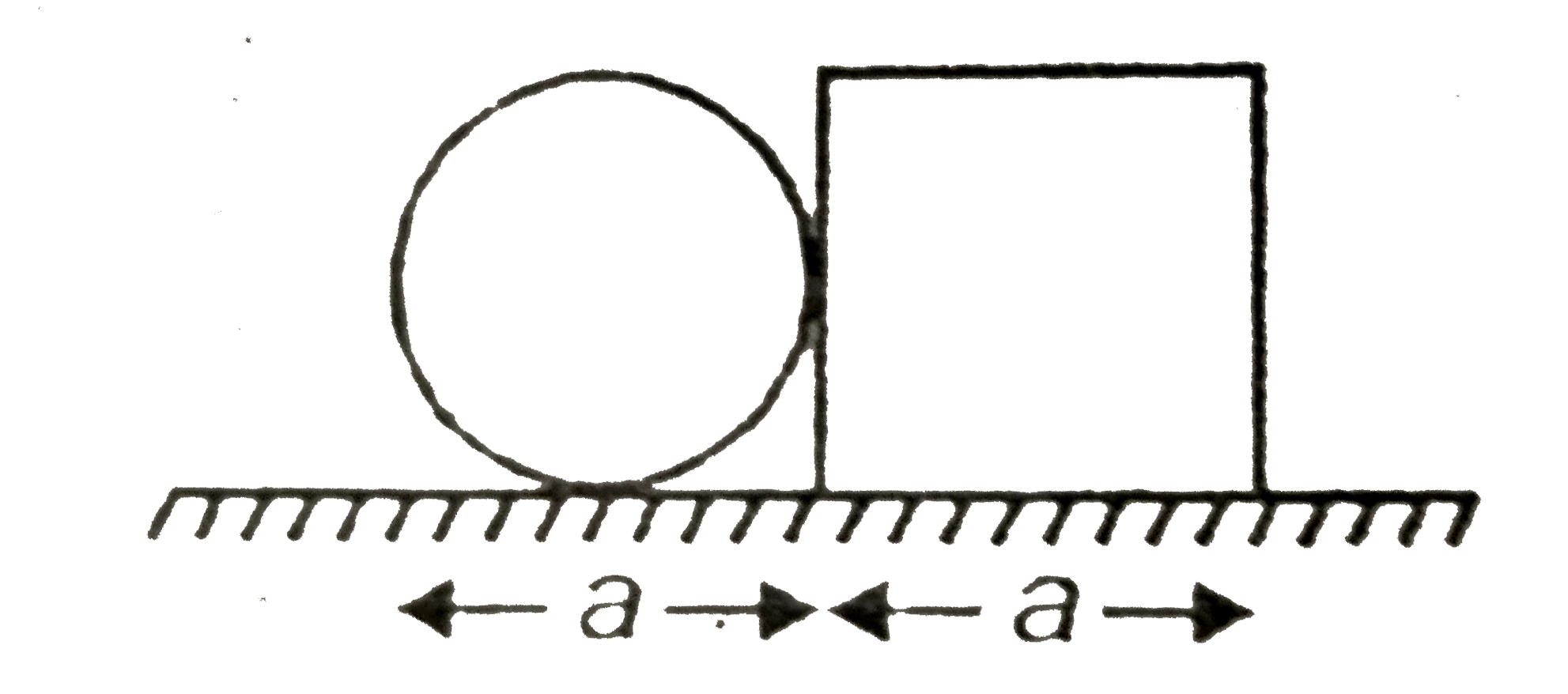
View SolutionA circular plate of diameter 'a' is kept in contact with a square plate of side a as shown. The density of the material and the thickness are same everywhere. The centre of mass of composite system will be
View Solution
