Find the centre of mass of a uniform plate having semicircular inner and outer boundaries of radii R1andR2.
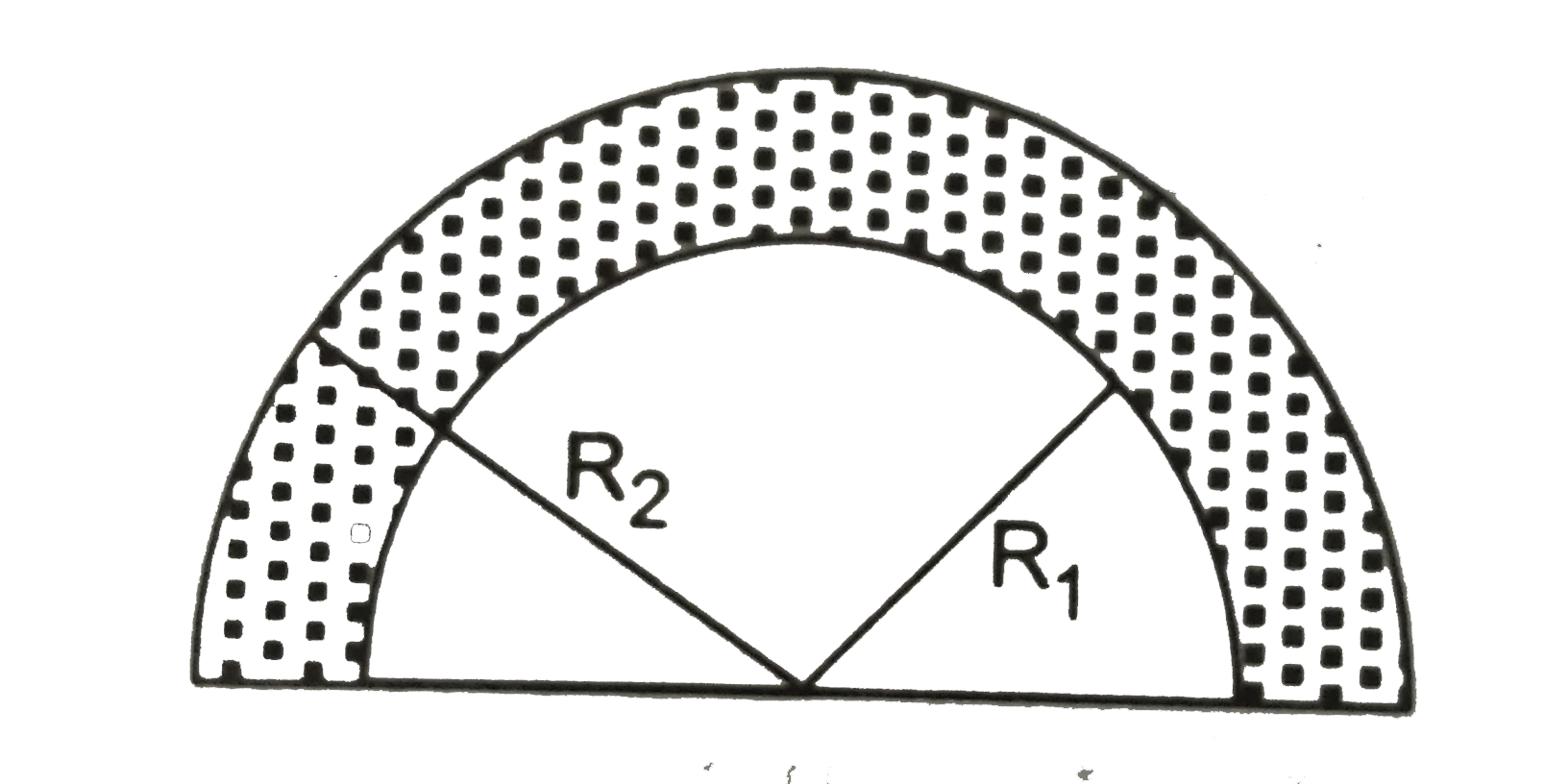
ycm=∫ydmM
or dm=MπrdrπR22−R212
MR22−R21/2
yCM=∫R_1R_2(2rπ).MR22−R21/2.rdrM
=2πR22−R212∫R_1R_2r2dr
=2πR22−R212[R32−R313]
=(4R21+R1R2+R223π(R1+R2)
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Question For short Answer25videos
CENTRE OF MASS, LINEAR MOMENTUM, COLLISION
- BOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -211videos
CENTRE OF MASS, LINEAR MOMENTUM, COLLISION
- BOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -118videos
CENTRE OF MASS, LINEAR MOMENTUM, COLLISION
- BOOK - HC VERMA ENGLISHCHAPTER - CALORIMETRYEXERCISE - Short answer9videos
CALORIMETRY
- BOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Question for short Answer10videos
CIRCULAR MOTION
Similar Questions
Find the centre of mass of a uniform semicircular ring of radius R and mass M.
View SolutionDetermine the centre of mass of a uniform hemisphere of radius R.
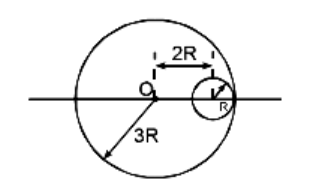
View SolutionIn the figure shown, find out centre of mass of a system of a uniform circular plate of radius 3R from O in which a hole of radius R is cut whose centre is at 2R distance from the centre of large circular plate
 View Solution
View SolutionA chance Q placed at thee center of a metallic spherical shell with inner and outer radii R1andR2 respectively . The normal component of the electric field at any point on the Gaussian surface with radius between R1andR2 will be
View SolutionFind coordinates of mass center of a uniform semicircular plate of radius r placed symmetric to the y-axis of a Cartesian coordinate system, with centre at origin.
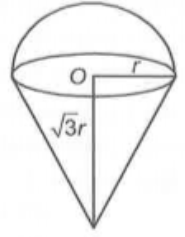
View SolutionA uniform solid hemisphere of radius r is joined to a uniform solid right circular cone of base radius r and height √3r. If both have same density, then find the position of centre of mass from centre of hemisphere
 View Solution
View SolutionA solenoid S1 is placed inside another solenoid S2 as shown in the fig. The radii of the inner and the outer solenoids are r1 and r2 respectively and the numbers of turns per unit length are n1 and n2 respectively. Consider a length I of each solenoid. Calculate the mutual inductance between them.
 View Solution
View SolutionA point charge Q is located at the centre of a hollow spherical conductor having inner radius as R1 and outer radius R2. The conductor being uncharged initially. The potential at the inner surface will be
View SolutionThe moment of inertia of a uniform semicircular wire of mass m and radius r, about an axis passing through its centre of mass and perpendicular to its plane is mr2(−kπ2). Find the value of k.
View SolutionThe moment of inertia of a uniform semicircular wire of mass 'M' and radius 'r' about a line perpendicular to the plane of the wire through the center is
View Solution

